Kapitel

Übungsaufgaben zur Berechnung mit dem Gauß-Jordan-Algorithmus
Berechne mit dem Gauß-Jordan-Algorithmus die inverse Matrix von:
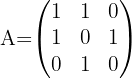
Berechne mit dem Gauß-Jordan-Algorithmus die inverse Matrix von:
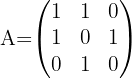
1 Erstelle eine Matrix vom Typ 

2 Nutze den Gauß-Jordan-Algorithmus, um die linke Hälfte, A, in die Einheitsmatrix umzuwandeln. Die Matrix, die auf der rechten Seite resultiert ist die inverse Matrix: A−1.
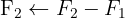


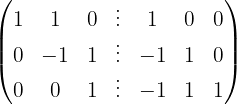
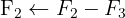



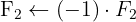

Die inverse Matrix ist:
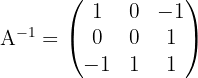
Berechne mit dem Gauß-Jordan-Algorithmus die inverse Matrix von:

Berechne mit dem Gauß-Jordan-Algorithmus die inverse Matrix von:

1 Erstelle eine Matrix vom Typ 

2 Nutze den Gauß-Jordan-Algorithmus, um die linke Hälfte, A, in die Einheitsmatrix umzuwandeln. Die resultierende Matrix auf der rechten Seite ist die inverse Matrix: A−1.
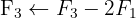






Inverse Matrix anhand der Determinanten berechnen
Bestimme anhand der Determinanten die inverse Matrix von:
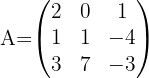
Bestimme anhand der Determinanten die inverse Matrix von:
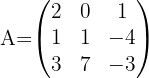
1 Wir erhalten die Determinante
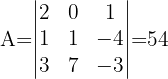
2 Wir erhalten die adjungierte Matrix
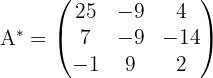
3 Wir erhalten die transponierte Matrix von 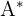

4 Wir dividieren die transponierte der adjungierten durch die Determinante:

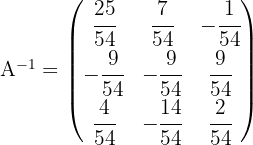
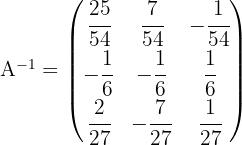
Werte bestimmen, bei denen es keine inverse Matrix gibt
Für welche Werte von  hat die Matrix
hat die Matrix 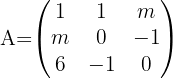 keine inverse Matrix?
keine inverse Matrix?
Für welche Werte von x hat die Matrix 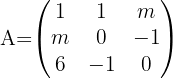 keine inverse Matrix?
keine inverse Matrix?
1 Wir berechnen die Determinante der Matrix

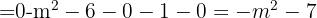
2 Wir setzen die Determinante gleich null und lösen die Gleichung
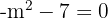
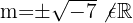
Somit hat die Matrix  eine inverse Matrix für irgendeinen reellen Wert von
eine inverse Matrix für irgendeinen reellen Wert von 
Für welche Werte von  hat die Matrix
hat die Matrix 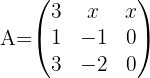 keine inverse Matrix?
keine inverse Matrix?
Für welche Werte von  hat die Matrix
hat die Matrix 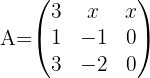 keine inverse Matrix?
keine inverse Matrix?
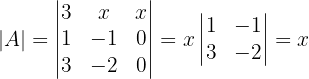
Für  hat die Matrix
hat die Matrix  keine inverse Matrix.
keine inverse Matrix.
Mit KI zusammenfassen:













