
Untersuchung des Monotonieverhaltens

1 Da es sich um ein Polynom handelt, ist die Definitionsmenge 
2 Wir leiten die Funktion ab
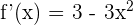
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
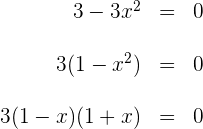
Wir erhalten  und
und 
4 Die oben genannten Werte unterteilen den Definitionsbereich in drei Intervalle:
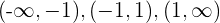
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 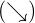 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
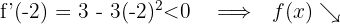
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
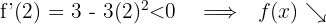
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich

Die Funktion ist streng monoton fallend im Bereich 
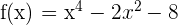
1 Da es sich um ein Polynom handelt, ist die Definitionsmenge 
2 Wir leiten die Funktion ab
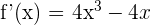
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Wir erhalten 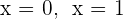 und
und 
4 Die oben genannten Werte unterteilen den Definitionsbereich in vier Intervalle:
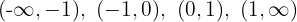
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 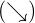 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
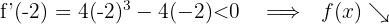
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für  nehmen wir
nehmen wir 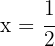 und setzen in die Ableitung ein
und setzen in die Ableitung ein
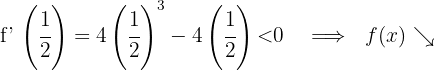
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
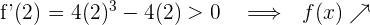
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 
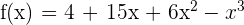
1 Da es sich um ein Polynom handelt, ist die Definitionsmenge 
2 Wir leiten die Funktion ab
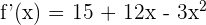
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Wir erhalten  und
und 
4 Die oben genannten Werte unterteilen den Definitionsbereich in drei Intervalle:
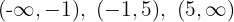
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 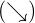 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
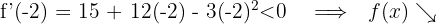
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für 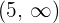 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
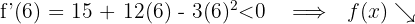
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 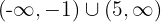

1 Da es sich um ein Polynom handelt, ist die Definitionsmenge 
2 Wir leiten die Funktion ab
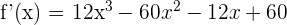
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
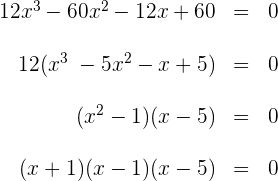
Wir erhalten  und
und 
4 Die oben genannten Werte unterteilen den Definitionsbereich in vier Intervalle:
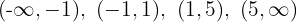
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 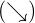 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
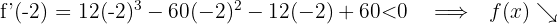
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für 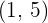 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
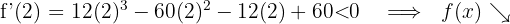
Für 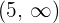 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 
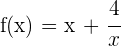
1 Die Definitionsmenge ist 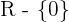
2 Wir leiten die Funktion ab

3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Wir erhalten 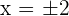
4 Die vorherigen Intervalle, zusammen mit  , teilen den Definitionsbereich in vier Intervalle:
, teilen den Definitionsbereich in vier Intervalle:
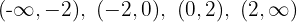
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 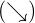 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für 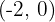 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
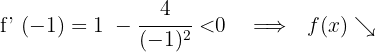
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
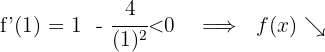
Für 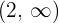 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
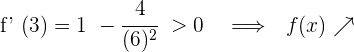
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 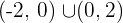
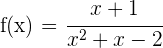
1 Der Nenner wird 0 für 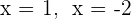 , weshalb der Definitionsbereich
, weshalb der Definitionsbereich 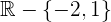 ist
ist
2 Wir leiten die Funktion ab

3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
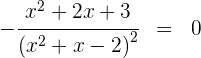
der Zähler wird innerhalb der reellen Zahlen nicht 0, da seine Determinante negativ ist.
4 Damit bleibt nur, den Definitionsbereich zu untersuchen:
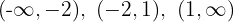
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 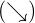 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
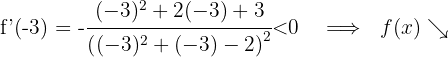
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
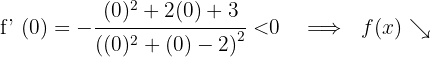
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
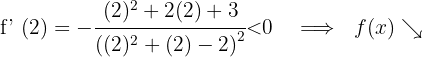
6 Daraus folgt:
Die Funktion ist im gesamten Definitionsbereich 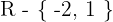 streng monoton fallend.
streng monoton fallend.

1 Der Nenner wird 0 für  , weshalb der Definitionsbereich
, weshalb der Definitionsbereich 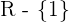 ist
ist
2 Wir leiten die Funktion ab

3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
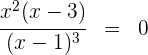
Wir erhalten 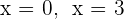 .
.
4 Die Werte, zusammen mit  , teilen den Definitionsbereich in vier Intervalle:
, teilen den Definitionsbereich in vier Intervalle:
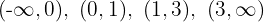
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 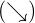 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
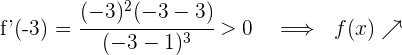
Für  nehmen wir
nehmen wir 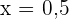 und setzen in die Ableitung ein
und setzen in die Ableitung ein
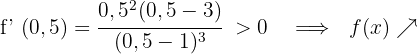
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
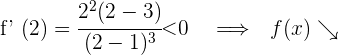
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
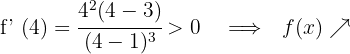
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 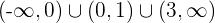
Die Funktion ist streng monoton fallend im Bereich 
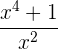
1 Der Nenner wird 0 für  , weshalb der Definitionsbereich
, weshalb der Definitionsbereich 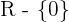 ist
ist
2 Wir leiten die Funktion ab
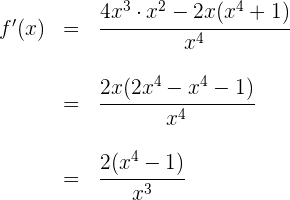
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
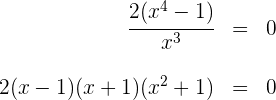
Wir erhalten  .
.
4 Die Werte, zusammen mit  , teilen den Definitionsbereich in vier Intervalle:
, teilen den Definitionsbereich in vier Intervalle:
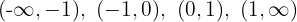
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 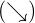 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
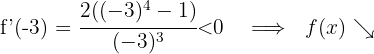
Für  nehmen wir
nehmen wir 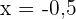 und setzen in die Ableitung ein
und setzen in die Ableitung ein
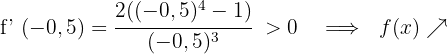
Für  nehmen wir
nehmen wir 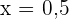 und setzen in die Ableitung ein
und setzen in die Ableitung ein
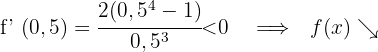
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
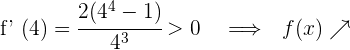
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 
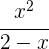
1 Der Nenner wird 0 für  , weshalb der Definitionsbereich
, weshalb der Definitionsbereich 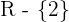 ist
ist
2 Wir leiten die Funktion ab

3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
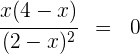
Wir erhalten 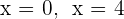 .
.
4 Die vorherigen Werte, zusammen mit  , teilen den Definitionsbereich in vier Intervalle:
, teilen den Definitionsbereich in vier Intervalle:
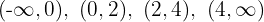
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 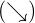 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
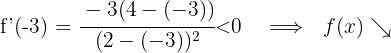
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
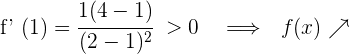
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
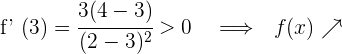
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
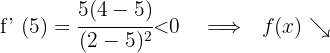
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 
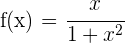
1 Der Nenner wird nicht 0, weshalb der Definitionsbereich  ist
ist
2 Wir leiten die Funktion ab
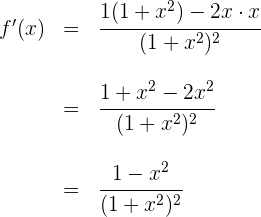
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
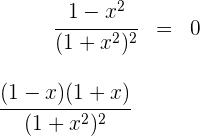
Wir erhalten  .
.
4 Die vorherigen Intervalle teilen den Definitionsbereich in drei Intervalle:
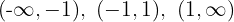
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 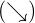 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
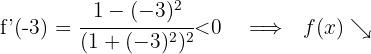
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
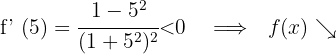
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 

1 Der Definitionsbereich besteht aus den Werten, bei denen der Radikand größer oder gleich 0 ist, also ist der Definitionsbereich 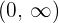
2 Wir leiten die Funktion ab

3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

wir erhalten 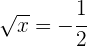 , was keine Lösung hat.
, was keine Lösung hat.
4 Nur der Definitionsbereich muss als Ganzes muss untersucht werden:
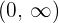
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 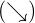 .
.
Für 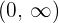 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
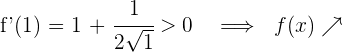
6 Daraus folgt:
Die Funktion ist in ihrem gesamten Definitionsbereich 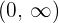 streng monoton steigend
streng monoton steigend
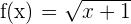
1 Der Definitionsbereich besteht aus den Werten, bei denen der Radikand größer oder gleich 0ist, also ist der Definitionsbereich 
2 Wir leiten die Funktion ab

3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
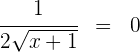
Es gibt keine Lösung.
4 Wir müssen nur den Definitionsbereich als Ganzes untersuchen:

5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 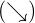 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
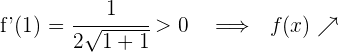
6 Daraus folgt:
Die Funktion ist in ihrem gesamten Definitionsbereich  streng monoton steigend.
streng monoton steigend.
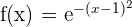
1 Da es sich um eine Exponentialfunktion handelt, ist die Definitionsmenge 
2 Wir leiten die Funktion ab
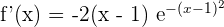
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Wir erhalten 
4 Die vorherigen Intervalle teilen den Definitionsbereich in zwei Intervalle:
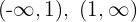
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 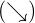 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
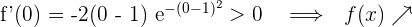
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
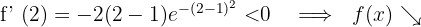
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 
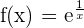
1 Der Exponent ist für  nicht definiert. Somit lautet die Definitionsmenge
nicht definiert. Somit lautet die Definitionsmenge 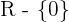
2 Wir leiten die Funkion ab
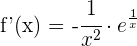
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
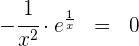
Es gibt keine Lösung in 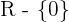
4 Der Definitionsbereich besteht aus zwei Intervallen:
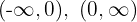
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 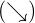 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
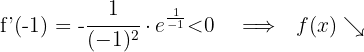
Für 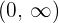 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
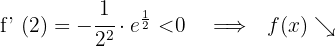
6Daraus folgt:
Die Funktion ist streng monoton fallend im Bereich 

1 Die Definitionsmenge ist 
2 Wir leiten die Funktion ab
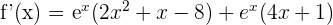
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
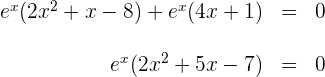
Daraus erhalten wir 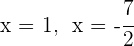
4 Die vorherigen Werte teilen den Definitionsbereich in drei Intervalle:
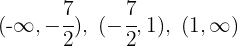
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 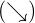 .
.
Für 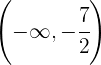 nehmen wir
nehmen wir 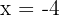 und setzen in die Ableitung ein
und setzen in die Ableitung ein
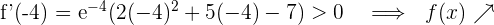
Für 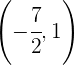 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
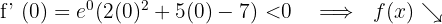
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 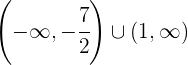
Die Funktion ist streng monoton fallend im Bereich 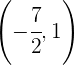

1 Die Definitionsmenge ist 
2 Wir leiten die Funktion ab
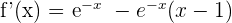
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Daraus erhalten wir 
4 Der vorherige Wert teilt den Definitionsbereich in zwei Intervalle:
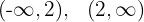
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 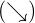 .
.
Para 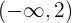 tomamos
tomamos  und setzen in die Ableitung ein
und setzen in die Ableitung ein
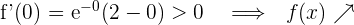
Para  tomamos
tomamos  und setzen in die Ableitung ein
und setzen in die Ableitung ein
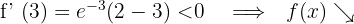
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 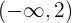
Die Funktion ist streng monoton fallend im Bereich 
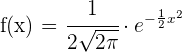
1 Die Definitionsmenge ist 
2 Wir leiten die Funktion ab
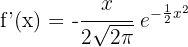
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Daraus erhalten wir 
4 Der vorherige Wert teilt den Definitionsbereich in zwei Intervalle:
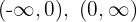
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 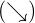 .
.
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
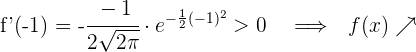
Für 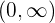 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
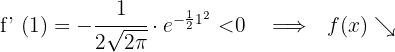
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 
Die Funktion ist streng monoton fallend im Bereich 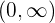

1 Die Definitionsmenge ist 
2 Wir leiten die Funktion ab
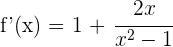
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf

Daraus erhalten wir unter Anwendung der Formel für quadratische Gleichungen 
4 Der vorherige Wert teilt den Definitionsbereich in:
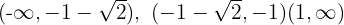
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend 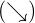 .
.
Für 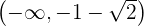 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

Für 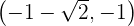 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
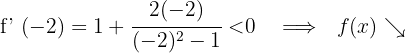
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein

6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 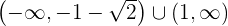
Die Funktion ist streng monoton fallend im Bereich 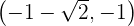
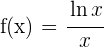
1 Die Definitionsmenge ist 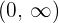
2 Wir leiten die Funktion ab
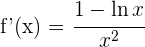
3 Wir setzen die Ableitung gleich 0 und lösen nach  auf
auf
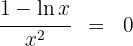
Daraus erhalten wir 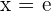
4 Der vorherige Wert teilt den Definitionsbereich in:
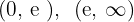
5 Wir untersuchen das Vorzeichen der Ableitung auf jedem Intervall: Wenn es positiv ist, ist die Funktion streng monoton steigend  ; wenn es negativ ist, ist die Funktion streng monoton fallend
; wenn es negativ ist, ist die Funktion streng monoton fallend  .
.
Für 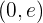 nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
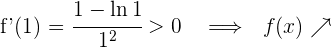
Für  nehmen wir
nehmen wir  und setzen in die Ableitung ein
und setzen in die Ableitung ein
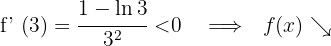
6 Daraus folgt:
Die Funktion ist streng monoton steigend im Bereich 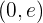
Die Funktion ist streng monoton fallend im Bereich 
Mit KI zusammenfassen:












