Kapitel

Was ist der Median?
Der Median ist der Wert, der genau in der Mitte einer Datenreihe liegt, die aufsteigend geordnet sind.
Der Median wird wie folgt dargestellt: 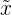
Der Median kann nur für quantitative Variablen bestimmt werden.
Beispiel für eine einfache Berechnung des Medians
1 Wir ordnen die Daten aufsteigend.
2 Wenn die Reihe eine ungerade Anzahl von Daten enthält, ist der Median der Wert in der Mitte der Reihe
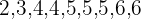
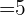
3 Wenn die Reihe eine gerade Anzahl von Daten enthält, ist der Median der Wert in der Mitte der beiden mittleren Werten.
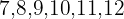
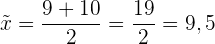
Formel für die Berechnung des Medians von gruppierten Daten
Der Median liegt in dem Intervall, in dem die kumulierte Häufigkeit die Hälfte der Summe der absoluten Häufigkeiten beträgt.
Das heisst, wir müssen das Intervall suchen, in dem er sich befindet.
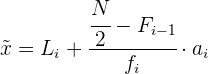
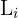 ist die Untergrenze der Klasse, in der der Median liegt
ist die Untergrenze der Klasse, in der der Median liegt
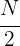 ist die halbe Summe der absoluten Häufigkeiten
ist die halbe Summe der absoluten Häufigkeiten
 ist die absolute Häufigkeit der medianen Klasse
ist die absolute Häufigkeit der medianen Klasse
 ist die kumulierte Häufigkeit vor der medianen Klasse
ist die kumulierte Häufigkeit vor der medianen Klasse
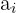 ist die Klassenbreite
ist die Klassenbreite
Der Median ist von den Klassenbreiten der Intervalle unabhängig
Beispiel für die Berechnung des Medians für die statistische Verteilung
Berechne den Median einer statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| fi | |
|---|---|
| [60,63) | 5 |
| [63,66) | 18 |
| [66,69) | 42 |
| [69,72) | 27 |
| [72,75) | 8 |
Wir suchen das Intervall, in dem der Median liegt. Hierzu dividieren wir  durch
durch  , da der Median der Wert in der Mitte ist.
, da der Median der Wert in der Mitte ist.
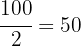
Wir suchen in der Spalte der kumulierten Häufigkeiten 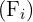 das Intervall, das
das Intervall, das  enthält
enthält
Mediane Klasse: 
Wir wenden die Formel zur Berechnung des Medians von gruppierten Daten an und extrahieren folgende Daten:
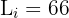
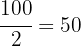
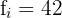

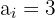
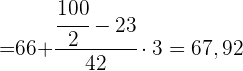
Mit KI zusammenfassen:













