Kapitel
- Defintionsbereich einer Funktion
- Komposition von Funktionen und Umkehrfunktion
- Monotonieverhalten von Funktionen
- Beschränkte Funktionen
- Maxima und Minima von Funktionen
- Konkavität, Konvexität und Wendepunkte
- Symmetrie von Funktionen
- Periodische Funktionen
- Schnittpunkte mit den Achsen
- Asymptoten
- Parabeläste
Defintionsbereich einer Funktion
Der Definitionsbereich einer Funktion besteht aus allen Elementen, die eine Abbildung haben. Das heißt, es sind die Werte von 
, die wir in die Korrespondenzregel einer Funktion einsetzen können, um den entsprechenden Wert von 
zu erhalten. Es gilt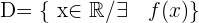
Das heißt, der Definitionsbereich einer Funktion sind die Werte von , die zu den reellen Zahlen gehören, für die es einen zugehörigen Wert der Funktion gibt.
Defintionsbereich der Polynomfunktion
Der Definitionsbereich einer Polynomfunktion ist 
, da jede reelle Zahl eine Abbildung hat. Das heißt,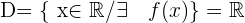
,
wobei 
eine Polynomfunktion ist.
Defintionsbereich der rationalen Funktion
Der Definitionsbereich ist abzüglich der Werte, für die der Nenner 0 wird.
Defintionsbereich der Wurzelfunktion mit ungeradem Wurzelexponenten
Der Definitionsbereich ist der Definitionsbereich der Wurzelfunktion, zum Beispiel
1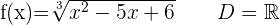 
2 
Defintionsbereich der Wurzelfunktion mit geradem Wurzelexponenten
Der Definitionsbereich besteht aus allen Werten, durch die der Radikand größer als oder gleich 0 wird.
Defintionsbereich der Logarithmusfunktion
Der Definitionsbereich besteht aus allen Werten, durch die die Funktion innerhalb des Logarithmus größer als 0 wird.
Defintionsbereich der Exponentialfunktion
Der Definitionsbereich ist der Definitionsbereich der Exponentialfunktion.
Defintionsbereich der Sinusfunktion
Der Definitionsbereich der Sinusfunktion ist
Defintionsbereich der Kosinusfunktion
Der Definitionsbereich der Kosinusfunktion ist
Defintionsbereich der Tangensfunktion
Defintionsbereich der Kotangensfunktion
Defintionsbereich der Sekansfunktion
Defintionsbereich der Kosekansfunktion
Defintionsbereich beim Rechnen mit Funktionen
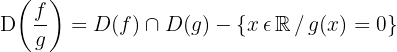
Komposition von Funktionen und Umkehrfunktion
Wir haben zwei Funktionen: und 
. Der Definitionsbereich der letzteren wird in die Wertemenge der ersteren einbezogen und es kann kann eine neue Funktion definiert werden, die jedem Element des Definitionsbereichs von den Wert von 
zuordnet. Dies ist eine Komposition von Funktionen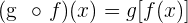 
.
Die Definitionsmenge der Komposition von Funktionen wird wie folgt definiert:
Die Umkehrfunktion von wird als eine andere Funktion 
bezeichnet, für die gilt:
- Wenn
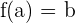, ist 
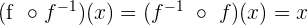
Berechnung der Umkehrfunktion
Um die Umkehrfunktion einer beliebigen Funktion zu bilden oder zu berechnen, müssen folgende Schritte durchgeführt werden:
1 Die Gleichung der Funktion wird in und 
geschrieben.
2 Die Variable wird in Funktion der Variable ermittelt.
3 Die Variablen werden vertauscht.
Monotonieverhalten von Funktionen
Monton steigende Funktion
steigt in 
nur dann monoton, wenn es eine Umgebung von gibt, sodass für alle , die zur Umgebung von gehören, gilt: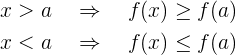
Monton fallende Funktion
fällt in nur dann, wenn es eine Umgebung von gibt, sodass für alle , die zur Umgebung von gehören, gilt:
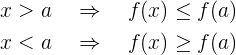
Beschränkte Funktionen
Nach oben beschränkte Funktion
Eine Funktion ist nach oben beschränkt, wenn es eine reelle Zahl 
gibt, sodass für alle 
ist. wird als die obere Schranke bezeichnet.
Nach unten beschränkte Funktion
Eine Funktion ist nach unten beschränkt, wenn es eine reelle Zahl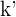 
gibt, soass für alle 
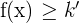ist. Die Zahl 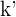wird als die untere Schranke bezeichnet.
Beschränkte Funktion
Eine beschränkte Funktion ist nach oben und nach unten beschränkt. Das heißt,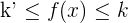
Maxima und Minima von Funktionen
Absolutes Maximum
Eine Funktion hat ihr absolutes Maximum bei 
, wenn die Ordinate größer oder gleich einem beliebigen anderen Punkt im Definitionsbereich der Funktion ist.
Absolutes Minimum
Eine Funktion hat ihr absolutes Minimum bei 
, wenn die Ordinate kleiner oder gleich einem beliebigen anderen Punkt im Definitionsbereich der Funktion ist.
Relatives Maximum und Minimum
Eine Funktion hat ein relatives Maximum im Punkt , wenn 
größer als oder gleich den Punkten in der Nähe des Punktes ist.
Eine Funktion hat ein relatives Minimum im Punkt 
, wenn 
kleiner oder gleich den Punkten in der Nähe des Punktes ist.
Es gibt Beziehungen zwischen den Ableitungen einer Funktion und ihren Maxima und Minima, die in der folgenden Tabelle zusammengefasst sind. Wenn du noch Fragen hast, kannst du dir die Theorie dazu ansehen.
Gegeben ist die ableitbare
Konkavität, Konvexität und Wendepunkte
Wenn und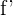 
ableitbare Funktionen bei sind, ist die Funktion:
konvex bei ,
wenn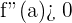 
.
konkav bei ,
wenn 
.
Die Wendepunkte einer Funktion sind die Punkte, an denen der Graph der Funktion seine Konkavität ändert, d. h. von konkav zu konvex oder umgekehrt wird.
Die folgende Tabelle/das folgende Diagramm fasst einige Ergebnisse in Bezug auf Konkavität und Wendepunkte zusammen.
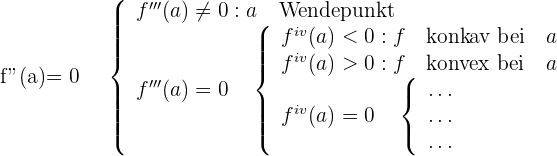
Symmetrie von Funktionen
Symmetrie zu den Achsen
Eine Funktion ist symmetrisch zum Urpsrung, wenn die Funktion gerade ist. Das heißt:
Symmetrie zum Ursprung
Eine Funktion ist symmetrisch zum Ursprung, wenn die Funktion ungerade ist. Das heißt:
Periodische Funktionen
Eine Funktion ist periodisch, Periode 
, wenn für jede ganze Zahl 
gilt, dass:
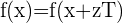
Wenn periodisch mit der Periode ist, so ist es auch 
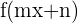und die Periode ist:
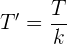
Schnittpunkte mit den Achsen
Schnittpunkte mit der x-Achse
Um die Schnittpunkte mit der x-Achse zu finden, nehmen wir 
und lösen die resultierende Gleichung.
Schnittpunkte mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu finden, nehmen wir 
und berechnen den Wert von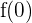 
.
Asymptoten
Asymptoten sind Geraden, denen sich die Funktion unbegrenzt nähert. Es gibt drei Arten von Asymptoten:
Horizontale Asymptoten
Wenn eine der beiden folgenden Bedingungen erfüllt ist
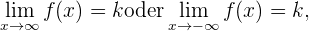
ist die Gerade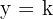 
eine horizontale Asmptote für den Graph von 
.
Vertikale Asymptoten
Wenn eine der beiden folgenden Bedingungen erfüllt ist
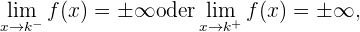
ist die Gerade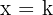 
eine vertikale Asmptote für den Graph von .
Schiefe Asymptoten
Schiefe Asymptoten gibt es nur, wenn es keine horizontalen Asymptoten gibt. Damit es eine schiefe Asymptote gibt, muss der Grad des Zählers genau einen Grad höher sein als der des Nenners, so dass die Asymptote gegeben ist durch
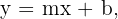
wobei
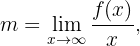
Parabeläste
Parabeläste gibt es nur, wenn: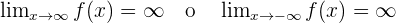
Parabelast in Richtung der y-Achse
hat einen Parabelast in Richtung der y-Achse, wenn:
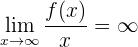
Dies bedeutet, dass sich der Graph wie eine Parabel mit einer vertikalen Achse verhält.
Parabelast in Richtung der x-Achse
hat einen Parabelast in Richtung der x-Achse, wenn:
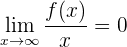
Dies bedeutet, dass sich der Graph wie eine Parabel mit einer horizontalen Achse verhält.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
