Was haben 0, π und e gemeinsam? Sie alle gehören zu den sogenannten besonderen Zahlen der Mathematik. Zahlen, die aus der Welt der Mathematik nicht wegzudenken sind. Manche von ihnen begegnen uns schon früh in der Schule, andere wirken auf den ersten Blick geheimnisvoll oder sogar unverständlich. Doch eines haben sie gemeinsam: Sie helfen uns, die Welt besser zu verstehen: sei es beim Rechnen mit Kreisen, bei komplexen Funktionen oder beim Aufbau unserer Zahlensysteme.
Bei uns lernst du einige dieser faszinierenden Zahlen kennen: Von der Null über die irrationale Kreiszahl Pi bis zur geheimnisvollen imaginären Einheit i. Wir erklären dir, was hinter diesen mathematischen Größen steckt, warum sie so besonders sind und wo sie in der Praxis eine Rolle spielen.
Unter all den Zahlen, die in der Geschichte der Mathematik besonders interessant sind, befindet sich die Zahl Null.
Die Zahl Null
Die Null wirkt auf viele wie „nichts“. Dabei steckt unglaublich viel Bedeutung in dieser besonderen Zahl. Mathematisch gesehen ist sie das neutrale Element der Addition und trennt die positiven von den negativen Zahlen. Sie ist die einzige reelle Zahl, die weder positiv noch negativ ist und damit ein echtes Unikat.
Unsere heutige Null verdanken wir der indischen Mathematik. Die alten Griechen hatten kein Konzept von „Nichts“ in Zahlenform. Erst indische Mathematiker führten im 5. Jahrhundert die Null als Zahl ein – das Sanskrit-Wort sunya bedeutet „leer“. Über die Araber gelangte die 0 schließlich nach Europa. Kaufleute und Wissenschaftler trugen dazu bei, dass sie sich trotz Widerstands der Kirche durchsetzte.
Auch mathematisch sorgt sie für Diskussionen: Man kann durch 0 nicht teilen, weil dabei kein eindeutiges Ergebnis herauskommt. Und 0 hoch 0? Je nach Sichtweise ergibt das 0, 1 oder „nicht definiert“. Auch spannend: Die Fakultät von 0, also 0!, ist 1. Eine Regel, die viele überrascht.
Als Symbol für Leere, Neuanfang oder Ewigkeit: Die Null ist weit mehr als „nichts“. Sie ist ein fundamentaler Baustein der Mathematik.
Definition und Verwendung der Zahl "e" in der Mathematik!
Die Zahl "e"? Was soll das sein? Die Zahl e ist eine der wichtigsten Konstanten in der Mathematik. Sie ist eine irrationale Zahl mit unendlich vielen, nicht periodischen Nachkommastellen. Ihr gerundeter Wert liegt bei e ≈ 2,71828.
Entdeckt wurde sie im 17. Jahrhundert im Zusammenhang mit Logarithmen durch John Napier. Später wurde sie durch den Schweizer Mathematiker Jakob Bernoulli populär, der bei der Zinseszins-Berechnung feststellte, dass der Zinswert bei unendlich vielen Berechnungsintervallen gegen die Zahl e strebt. Die exakte Definition von e als Basis des natürlichen Logarithmus erfolgte durch Leonhard Euler, der auch ihre Irrationalität nachwies.
Irrationale Zahlen sind Dezimalzahlen, die nicht als Bruch zweier ganzer Zahlen dargestellt werden können. Ihre Nachkommastellen sind unendlich lang und folgen keinem wiederkehrenden Muster – sie sind also nicht periodisch. Beispiele für irrationale Zahlen sind π (Pi), e (Eulersche Zahl) und die Quadratwurzel aus 2.
Im Gegensatz zu rationalen Zahlen wie 1/3=0,333..., die eine klare periodische Struktur besitzen, lassen sich irrationale Zahlen nicht exakt notieren. Man kann sie nur näherungsweise angeben. Ihre Entdeckung war ein Meilenstein in der Mathematikgeschichte!
Du brauchst Statistik Nachhilfe? Entdecke das Angebot von Superprof und finde deinen auf dich zugeschnittenen Kurs.
Mathematisch lässt sich e auch als unendliche Summe schreiben:
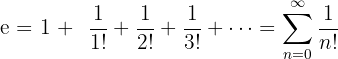
Die Zahl e begegnet uns in vielen Bereichen: bei Exponentialfunktionen, in der Zinsrechnung, in der Biologie (z. B. Populationswachstum), Physik, Informatik und Statistik. Immer dann, wenn Prozesse kontinuierlich wachsen oder zerfallen, spielt e eine zentrale Rolle.
Die Zahl i: Die Wurzel aus –1
Die imaginäre Zahl i ist eine der faszinierendsten Entdeckungen der Mathematik, denn sie macht das scheinbar Unmögliche möglich: Sie erlaubt es uns, die Wurzel aus einer negativen Zahl zu berechnen. Per Definition ist
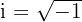
und damit gilt auch:
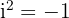
Das klingt im ersten Moment merkwürdig, denn in der Welt der reellen Zahlen gibt es keine Zahl, deren Quadrat negativ ist. Genau hier setzen die komplexen Zahlen an: Sie bestehen aus einem Realteil und einem Imaginärteil und haben die Form a+bia + bia+bi. So lassen sich auch Gleichungen lösen, die sonst keine reellen Lösungen hätten.
Du verstehst nur Bahnhof? Hier haben wir dir einmal die wichtigsten mathematischen Zahlensysteme und Begrifflichkeiten zusammengefasst:
| Begriff | Definition |
|---|---|
| Natürliche Zahlen (ℕ) | Alle positiven ganzen Zahlen, die zum Zählen verwendet werden (0, 1, 2, 3, …). |
| Ganze Zahlen (ℤ) | Alle natürlichen Zahlen und ihre negativen Gegenstücke (…, -3, -2, -1, 0, 1, 2, 3, …). |
| Rationale Zahlen (ℚ) | Alle Zahlen, die als Bruch zweier ganzer Zahlen geschrieben werden können (z. B. ½, -7/4, 0, 3). |
| Irrationale Zahlen | Zahlen mit unendlicher, nicht periodischer Dezimaldarstellung (z. B. π, √2, e), die nicht als Bruch darstellbar sind. |
| Reelle Zahlen (ℝ) | Umfassen alle rationalen und irrationalen Zahlen. Sie bilden die bekannte Zahlengerade. |
| Imaginäre Zahlen | Zahlen, die ein Vielfaches von √–1 (also i) sind, z. B. 2i oder –5i. Sie haben keine reelle Komponente. |
| Komplexe Zahlen (ℂ) | Kombination aus reellen und imaginären Zahlen: a + bi, wobei a und b reell sind und i = √–1 die imaginäre Einheit. |
| Transzendente Zahlen | Irrationale Zahlen, die nicht Nullstellen eines Polynoms mit rationalen Koeffizienten sind (z. B. π, e). |
| Algebraische Zahlen | Zahlen, die Nullstellen von Polynomen mit ganzzahligen Koeffizienten sind (z. B. √2, da √2 eine Lösung von x² – 2 = 0 ist). |
| Rein imaginäre Zahlen | Komplexe Zahlen ohne Realteil (z. B. 0 + 3i oder einfach 3i). |
Die Idee der imaginären Zahlen entstand im 16. Jahrhundert, als Mathematiker wie Cardano und Bombelli mit Gleichungen experimentierten, die keine offensichtliche Lösung hatten. Später wurde i von Leonhard Euler eingeführt und etablierte sich als festes mathematisches Konzept.
Heute ist i nicht nur in der Algebra wichtig, sondern auch in der Physik, Elektrotechnik und Signalverarbeitung. Die komplexen Zahlen, die sich aus der Einführung von i ergeben, ermöglichen neue Denkweisen, vereinfachen Rechnungen und erweitern unser Verständnis für mathematische Zusammenhänge – weit über das hinaus, was mit reellen Zahlen möglich wäre.
Wofür dient die Zahl Pi?
Was ist π überhaupt? Pi – geschrieben als π – ist eine mathematische Konstante und beschreibt das Verhältnis von Umfang zu Durchmesser eines Kreises:
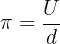
Diese Zahl ist irrational, also unendlich lang, ohne regelmäßiges Muster. Ihr gerundeter Wert 3,1416 reicht im Alltag meist völlig aus. In Mathematik, Physik und Technik begegnet dir π überall dort, wo es um Kreise, Kugeln oder Wellen geht, z. B. bei der Flächenberechnung, in der Trigonometrie oder bei Kreisbewegungen.
Was Pi besonders macht? Es ist nicht exakt darstellbar, nicht konstruierbar und sogar transzendent, also nicht Lösung irgendeiner algebraischen Gleichung. Seit Archimedes (3. Jh. v. Chr.) versuchen Menschen, immer mehr Nachkommastellen zu berechnen: heute sind es über 300 Billionen! Dennoch genügen schon 10 Stellen für die Erdvermessung.
Am 14. März wird der Pi-Day gefeiert. Ein Beweis dafür, dass diese unscheinbare Zahl weltweit Bewunderung auslöst.
Was ist der "goldene Schnitt" in Mathematik?
Der Goldene Schnitt ist ein besonderes Verhältnis zwischen zwei Streckenabschnitten: Der kleinere Teil verhält sich zum größeren so wie der größere zur gesamten Strecke. Dieses harmonische Verhältnis ergibt die irrationale Zahl Φ (Phi), die ungefähr 1,618 beträgt. Mathematisch lässt sich der Goldene Schnitt durch die Gleichung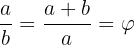 
ausdrücken.
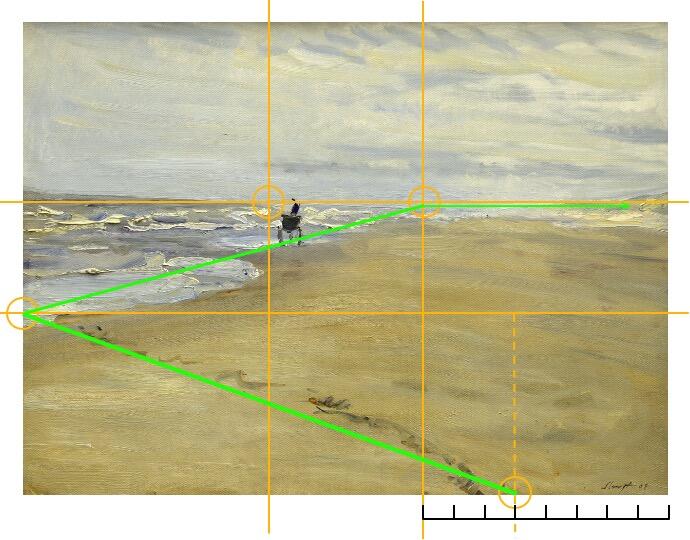
Bereits in der Antike wurde dieses Prinzip genuzt z. B. von Euklid in der Geometrie. Später entdeckte man es in der Fibonacci-Folge wieder. Mit zunehmender Zahlenfolge nähert sich das Verhältnis zweier benachbarter Zahlen immer weiter Phi an.
Doch der Goldene Schnitt ist nicht nur ein mathematisches Phänomen: Er begegnet uns in der Natur (z. B. Sonnenblumen, Schneckenhäuser), der Kunst, der Architektur (wie im Parthenon) und sogar in der Musik. Viele empfinden ihn als besonders ästhetisch – vielleicht, weil unser Gehirn Symmetrien und natürliche Proportionen besonders gern hat.
Was sind Primzahlen?
Eine Primzahl ist eine natürliche Ganzzahl, die nur zwei unterschiedliche Teiler zulässt: 1 und sich selbst. Daher sind 0 und 1 keine Primzahlen.
Primzahlen sind so etwas wie die Bausteine der Mathematik. Beispiele dafür sind 2, 3, 5, 7, 11 oder 13. Sie lassen sich nur durch 1 oder durch sich selbst teilen – ohne Rest.
Das Besondere: Jede natürliche Zahl lässt sich in Primzahlen zerlegen: dieser Prozess heißt Primfaktorzerlegung. Zum Beispiel:
60 = 2 × 2 × 3 × 5.
Diese Zerlegung hilft uns bei vielen Rechenwegen, z. B. beim größten gemeinsamen Teiler (ggT) oder dem kleinsten gemeinsamen Vielfachen (kgV).
Spannend ist auch das Sieb des Eratosthenes – eine clevere Methode, um Primzahlen zu finden. Es wird bis heute im Unterricht verwendet!
Und wusstest du, dass Primzahlen sogar in der Kryptografie zum Einsatz kommen? Sie helfen, Daten im Internet sicher zu verschlüsseln. Oder dass manche Zikadenarten nur alle 13 oder 17 Jahre auftauchen: beide Zahlen sind Primzahlen!
Du brauchst dringend Mathe Nachhilfe? Entdecke das Kursangebot von Superprof in deiner Stadt (z.B. Mathe Nachhilfe Bochum).
Was sind perfekte Zahlen?
Eine perfekte Zahl ist eine natürliche Zahl, bei der die Summe ihrer echten Teiler (also aller Teiler ohne die Zahl selbst) wieder die Zahl selbst ergibt. Klingt erstmal abstrakt, aber ein Beispiel macht’s klar: Die Teiler von 6 sind 1, 2 und 3. Addiert man diese, kommt man wieder auf 6: also ist 6 eine perfekte Zahl. Genauso funktioniert es mit 28 oder 496.
Schon in der Antike waren Mathematiker fasziniert von diesen Zahlen. Euklid beschrieb sie um 300 v. Chr. in seinem Werk Elemente. Später fand der große Mathematiker Euler heraus, dass alle geraden perfekten Zahlen mit sogenannten Mersenne-Primzahlen zusammenhängen – also Zahlen der Form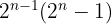 
, die selbst prim sind.
Bis heute kennt man nur 51 perfekte Zahlen, die größte davon wurde 2018 entdeckt und sie besteht aus über 23 Millionen Stellen! Ob es auch ungerade perfekte Zahlen gibt, ist bis heute eines der großen ungelösten Rätsel der Mathematik.
Und obwohl perfekte Zahlen keinen direkten praktischen Nutzen haben, gelten sie als echtes Mysterium und faszinieren die Forschung bis heute.
Auf Superprof findest du tolle Lehrer und Lehrerinnen für Mathe Nachhilfe!
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
