Mathematische Zeichen begegnen uns überall – in der Schule, im Alltag, in der Technik oder in der Wissenschaft. Sie sind die Sprache der Mathematik und ermöglichen es, komplexe Zusammenhänge klar und kompakt auszudrücken.
Ob ein Mathestudium schwer ist, hängt auch davon ab, ob Du die Grundlagen der Symbole und Schreibweisen beherrschst, um schnell, effizient und präzise Aussagen zu treffen. Doch was genau steckt hinter den verschiedenen mathematischen Symbolen?
In diesem Artikel werfen wir einen Blick auf die wichtigsten mathematischen Zeichen, erklären ihre Bedeutung und zeigen, wie sie in Formeln und Rechnungen verwendet werden.
Symbole der Logik
Ohne eine eigene Sprache kommen Mathematiker nicht aus, weshalb es wichtig ist, schon zu Beginn deines Studiums ein gutes Verständnis für die Zeichen zu entwickeln.
Junktoren
Starten wir mit den Zeichen, die dem logischen Verständnis dienen, welches Du bei Beweisen in der Mathematik benötigst.
Negation ("nicht")
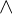Konjunktion ("und")
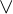Disjunktion ("oder")
Ein typisches Beispiel für die Verwendung wäre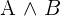 
, das sicher immer wieder vorkommt. Hier ist wichtig zu wissen, dass "oder" nicht ausschließend ist. Es bedeutet also nicht zwingend entweder/oder, sondern kann auch "und" bedeuten.
Diese Zeichen sind elementar im Mathe Studium an der Uni.
Quantoren
Nun kommen wir zu den Quantoren, die Du für Widerspruchsbeweise benötigst. Schau dir die wichtigsten an:
- Es gibt (mindestens) ein:
(Existenzquantor) - Es gibt genau ein:
(Existenzquantor) - Es gibt kein:
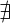(Existenzquantor) - Für alle:
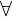(Allquantor)
Du braucht die sogenannten Quantoren, um anzugeben, für welche Objekte x einer Grundmenge eine Aussageform A(x) gilt. Schau dir das Beispiel an: Für alle x gilt, dass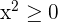 
. Dies können wir mit dem Allquantor tun, indem wir schreiben 
.
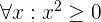Pfeile
In der Welt der Logik sind Pfeile wichtige mathematische Symbole. Schauen wir uns die wichtigsten an:
für die Implikation ("aus ... folgt ...")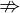
für das Gegenteil der Implikation („daraus folgt nicht“)
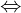für die Äquivalenz ("äquivalent zu... genau dann, wenn ...")
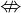für das Gegenteil der Äquivalenz („nicht genau dann wenn“)
Dies ist eine kleine Auswahl der wichtigsten Symbole. Diese Symbole gehören zur Voraussetzung für das Mathestudium.
Symbole für Aussagen der Logik
Hier kommen einige weitere logische Symbole, die Du kennen solltest:
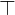Tautologie - immer wahr
Kontradiktion -immer falsch
Modellrelation - Aussage ist wahr in einem Modell
Ableitbarkeit - Aussage ist logisch ableitbar
Logische Äquivalenz - zwei Aussagen sind logisch gleichwertig
Mit diesen Symbole kannst Du wichtige Aussagen über die Logik treffen.
Symbole der Zahlenmengen
Im Mathestudium verwendest Du kaum mehr Zahlen wie in Mathe in der Schule, sondern drückst über die Symbole für Zahlen Mengen aus, welche Zahlen in eine Funktion eingesetzt werden können. Befasse dich also am besten direkt zu Beginn mit den mathematischen Symbolen für Mengen von Zahlen.
Du brauchst die Zahlenmengen, um zu beschreiben, mit welchen Zahlen man in einem bestimmten Anwendungsfall rechnen kann.
Vielleicht kennst du diese Symbole bereits aus der Mathe Nachhilfe München?
Schauen wir uns die wichtigen mathematischen Zeichen der Zahlenmenge an:
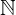= {1;2;3;4;…} ist die Menge der natürlichen Zahlen, zu denen etwa 1, 2, 3, 4, 5 gehören. Man benutzt sie, um auf natürliche Weise zu zählen.
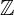= {0;−1;1;−2;2;…} sind die ganzen Zahlen und enthalten zudem die Null, die natürlichen Zahlen und ihre Gegenzahlen. 
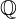= die rationalen Zahlen, zu denen neben den ganzen Zahlen auch Brüche gehören.
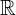= die reellen Zahlen umfassen alle Dezimalbrüche inklusive der rationalen Zahlen, aber auch nichtperiodischer Dezimalbrüche mit unendlich vielen Nachkommastellen. Dazu gehören auch e und π.
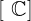= die komplexen Zahlen umfassen neben allen schon genannten Zahlen auch eine imaginäre Zahl i.
Du siehst also, die elementaren Zahlenmengen bauen aufeinander auf, man könnte also auch schreiben N ⊂ Z ⊂ Q ⊂ R ⊂ C. Denn jede Zahlenmenge ist in der nächsten Gruppe enthalten.
Übrigens ist eine gute Vorbereitung für den Start ins Mathestudium sehr wichtig.
Symbole der Mengenlehre
Die Mengenlehre ist ein grundlegender Zweig der Mathematik, der sich mit der Beschreibung, dem Vergleich und der Verknüpfung von Mengen – also Sammlungen von unterscheidbaren Objekten – befasst. Die Elemente einer Menge können Zahlen, Buchstaben, Menschen oder auch andere Mengen sein.
Typischerweise werden für Mengen Großbuchstaben gewählt und für die Elemente einer Menge Kleinbuchstaben.
In der Mathematik versteht man unter einer Menge jede Zusammenfassung von verschiedenen Objekten zu einer Gesamtheit. Elemente einer Menge sind dann die Objekte, die zu einer Menge gehören.
Mit diesen Symbolen im Kopf ist das Mathestudium nicht so schwer!
Die wichtigsten Zeichen der Mengenlehre haben wir zusammengestellt:
- Mengenklammern:
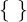wobei man liest "Menge aller..., für die gilt..." - Element von:
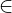Beispiel: a 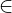A: a ist ein Element der Menge A - Kein Element von:
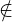Beispiel: b 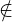B: b gehört nicht zu B - Teilmenge:
Beispiel: A B: A ist Teilmenge von B - Obermenge:
Beispiel: B A: B enthält A - Vereinigung:
Beispiel: A B: Alle Elemente aus A oder B - Mengendifferenz:
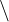Beispiel: A 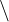B: Elemente in A, aber nicht in B - Mächtigkeit:
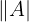
- Leere Menge:
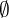Eine Menge ohne Elemente
So gelingt übrigens die Vorbereitung auf die nächste Matheklausur!
Symbole zum Rechnen und Vergleichen
Rechenzeichen sind in der Mathematik von grundlegender Bedeutung, da sie dazu dienen, operationale Beziehungen zwischen Zahlen, Variablen und Ausdrücken darzustellen. Kommen wir zu den wichtigsten Rechenzeichen, die Du für alle möglichen Berechnung nutzen kannst.
Rechenzeichen
Ohne Rechenzeichen wären mathematische Ausdrücke schwer verständlich. Rechenzeichen geben an, wie Zahlen miteinander kombiniert oder verglichen werden sollen.
Schauen wir uns zunächst die ganz grundlegende Symbole an:
- Addition:
- Subtraktion:
- Multiplikation:
- Division:
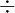
- Bruch:
- Wurzel:
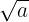
- Prozent:
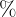
Diese Zeichen nutzt man für ganz klassische Berechnungen.
Mathe Zeichen zum Vergleichen
Wenn man Zahlen, Mengen oder Ergebnisse vergleichen möchte, dann kann man auch dazu bestimmte Symbole nutzen. Die sogenannten Vergleichsoperatoren kommen immer wieder vor:
- Gleich:
- Ungleich:
- Kleiner als:
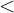
- Größer als:
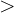
- Kleiner gleich:
- Größer gleich:
Beachte diese Symbole beim Lernen für das Mathestudium.
Symbole für Funktionen
Symbole von Funktionen sind in der Mathematik unverzichtbar, da sie eine präzise und effiziente Darstellung und Analyse von Beziehungen zwischen Variablen ermöglichen. Sie sind grundlegende Werkzeuge, um mathematische Modelle zu formulieren und komplexe Sachverhalte verständlich zu machen.
Die folgende Symbole sind von zentraler Bedeutung, insbesondere in der Analysis, um Funktionen zu beschreiben und mit ihnen zu arbeiten.
- Funktionsbezeichnung:
→ Eine Funktion, die die Variable x als Eingabe hat. - Funktionswert:
→ Der Funktionswert, der entsteht, wenn x=a. - Definition einer Funktion:
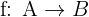→ Eine Funktion f, die Elemente aus der Menge A auf die Menge B abbildet. - Ableitung einer Funktion:
→ Die Ableitung von f(x) nach x, die die Steigung der Funktion an einem bestimmten Punkt beschreibt. - Umkehrfunktion:
→ Funktion, die eine gegebene Funktion umkehrt. - Integral einer Funktion:
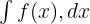→ Das Integral einer Funktion f(x), das die Fläche unter der Kurve darstellt. - Grenzwert einer Funktion:
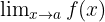→ Der Grenzwert der Funktion f(x) für x→a. - Abbildungspfeil:
→ - Zuordnungspfeil:
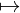→ beschreibt Zuordnungen
Die Symbole lernst Du auch in Nachhilfe Mathe.
Symbole der Geometrie und Vektoren
In der Geometrie sind die Symbole wichtig, um Punkte, Linien, Winkel und Flächen zu beschreiben und mathematische Beziehungen zwischen geometrischen Objekten zu formulieren.
Geometrie
Schauen wir uns die wichtigsten Symbole an:
- Gerade:
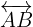Eine unendlich lange Gerade, die durch die Punkte A und B definiert ist. - Strecke:
Eine begrenzte Strecke zwischen den Punkten A und B. - Winkel:
Der Winkel zwischen den Vektoren, gemessen in Grad. - Rechter Winkel:
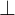Bezeichnet senkrechte Linien oder Vektoren, die einen Rechten Winkel zueinander bilden. - Parallelität:
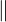Wird verwendet, um parallel verlaufende Linien oder Vektoren zu kennzeichnen, die denselben Richtungsvektor haben. - Kreisradius:
Der Radius eines Kreises, der den Abstand vom Mittelpunkt des Kreises zu einem Punkt auf dem Rand des Kreises angibt. - Fläche eines Kreises:
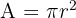Die Fläche eines Kreises, wobei r der Radius ist.
Einige dieser Symbole solltest Du noch aus der Schule kennen.
Vektorrechnung
In der Vektorrechnung sind die Symbole wesentlich, um mit Vektoren, Skalarprodukten, Vektorprodukten und Linearkombinationen zu arbeiten. Hier kommen die am häufigsten genutzten:
- Vektor:
Ein Vektor wird oft durch einen Pfeil über einem Buchstaben bezeichnet. Er hat sowohl eine Richtung als auch eine Größe. - Skalarprodukt:
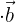Das Skalarprodukt zweier Vektoren, das eine Zahl (Skalar) ergibt und oft verwendet wird, um den Winkel zwischen den Vektoren zu bestimmen. - Vektorprodukt:
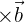Das Vektorprodukt zweier Vektoren, das einen neuen Vektor ergibt, der senkrecht auf der Ebene der beiden ursprünglichen Vektoren steht. - Richtungsvektor:
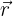Ein Richtungsvektor beschreibt die Richtung einer Linie oder eines Vektors.
Diese Zeichen lernst Du in der Mathe Nachhilfe Hamburg!
Griechische Buchstaben
Schließlich kommen wir zu einigen griechischen Symbolen, die weit verbreitet in der Mathematik sind, insbesondere in der Algebra, Analysis und Geometrie. Sie werden häufig verwendet, um konstante Werte, Variablen, Funktionen, Operatoren und Mengen darzustellen.
Schauen wir uns die wichtigsten an:
- Alpha:
Wird häufig für Winkel oder als Parameter in Gleichungen verwendet. - Beta:
Oft verwendet in der Statistik und Wahrscheinlichkeitsrechnung etwa für Regressionskoeffizienten. - Gamma:
Wird in der Analysis oder für die Innenwinkel eines Dreiecks genutzt. - Delta:
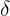Repräsentiert eine kleine Änderung oder Differenz (Differential oder Variation). - Epsilon:
. Wird in der Analysis verwendet, um einen beliebig kleinen Wert darzustellen (Definition von Grenzwerten). - Pi:
Das berühmte Symbol für die Kreiszahl, das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. - Sigma:
Häufig verwendet als Summenzeichen oder als Standardabweichung in der Statistik.
Bei jedem Studiengang mit Mathe wirst Du diesen Symbolen immer wieder über den Weg laufen.
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
