Mathematische Formeln sind das Fundament jeder naturwissenschaftlichen und technischen Disziplin. Und da Mathe einfach allgegenwärtig ist, sollte man die wichtigsten mathematischen Formeln kennen.
Sie helfen uns, komplexe Zusammenhänge klar auszudrücken und Probleme systematisch zu lösen. Ob in der Geometrie, Algebra oder Physik, Formeln vereinfachen die Welt der Zahlen und ermöglichen präzise Berechnungen.
| Formel | Kurzbeschreibung / Bedeutung | Variablen / Hinweise |
|---|---|---|
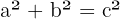 | Pythagoras: Beziehung der Seiten in einem rechtwinkligen Dreieck. |  Katheten, Katheten,  Hypotenuse Hypotenuse |
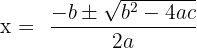 | Quadratische Formel: Lösungsformel für  . . | Diskriminante 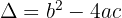 ; reelle Lösungen, wenn ; reelle Lösungen, wenn 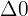 . . |
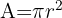 | Flächeninhalt eines Kreises. |  Radius; Radius; 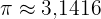 |
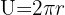 | Umfang eines Kreises. |  Radius Radius |
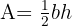 | Flächeninhalt eines Dreiecks (Grundlinie × Höhe / 2). |  Basis, Basis,  Höhe senkrecht zu Höhe senkrecht zu  |
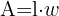 | Flächeninhalt eines Rechtecks. |  Länge, Länge,  Breite Breite |
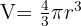 | Volumen einer Kugel. |  Radius Radius |
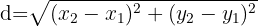 | Distanz zwischen zwei Punkten in der Ebene (euklidische Entfernung). | 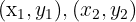 Punkte Punkte |
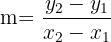 | Steigungsformel einer Geraden durch zwei Punkte. |  Steigung; Steigung;  |
 | Lineare Gleichung in der Geradenform (Steigung–Achsenabschnitt). |  Steigung, Steigung,  y-Achsenabschnitt y-Achsenabschnitt |
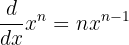 | Potenzregel der Differentialrechnung (Ableitung). |  reelle Zahl reelle Zahl |
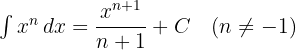 | Stammfunktion/Integral der Potenzfunktion. |  Integrationskonstante Integrationskonstante |
Es gibt zahlreiche Gleichungen, die ihre Zeit geprägt und die Vision auf die Mathematik, die Wissenschaft allgemein oder sogar die Welt stark verändert haben. Schauen wir uns in diesem Artikel also die wichtigsten Formeln aus der Welt der Mathematik an!

Binomische Formeln
Die binomischen Formeln sind wichtige Rechenregeln der Algebra, die das Ausmultiplizieren und Zusammenfassen von Termen vereinfachen, in denen Summen oder Differenzen von zwei Variablen vorkommen.
Finde mit Superprof die passende Mathe Nachhilfe Berlin.
Sie werden auch als Quadrat- und Produktformeln bezeichnet.
Erste binomische Formel
Die erste binomische Formel besagt: Das Quadrat einer Summe ist gleich der Summe aus dem Quadrat des ersten Summanden, dem doppelten Produkt beider Summanden und dem Quadrat des zweiten Summanden.
Formel: 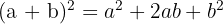
Beispiel: 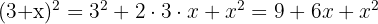
Hier steht ein Plus in Klammern.
Zweite binomische Formel
Die zweite binomische Formel besagt: Das Quadrat einer Differenz ist gleich der Summe aus dem Quadrat des ersten Summanden, minus dem doppelten Produkt beider Summanden und dem Quadrat des zweiten Summanden.
Für mehr Durchblick hilft Mathe Nachhilfe für Studenten.
Formel: 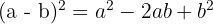
Beispiel: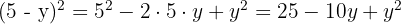
Hier geht es also darum, wenn ein Minus in der Klammer steht.
Dritte binomische Formel
Die dritte binomische Formel besagt: Das Produkt einer Summe und einer Differenz ist gleich der Differenz der Quadrate der beiden Summanden.
Formel: 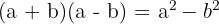
Beispiel: 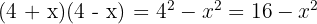
Das sind mathematische Formeln, die Du auf jeden Fall im Unterricht benötigst.
Formeln der Geometrie
Die Geometrie ist der Teil der Mathematik, der sich mit Formen, Größen, Figuren und ihren Eigenschaften beschäftigt. Um Flächen, Umfänge und Volumen zu berechnen, werden Formeln verwendet, die je nach Figur unterschiedlich sind.

Durch Mathe Nachhilfe kannst Du die Verwendung dieser Formeln lernen.
Formeln zur Flächenberechnung
Kommen wir zu den mathematischen Formeln zur Flächenberechnung unterschiedlicher geometrischer Formen:
- Rechteck:
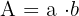
- Quadrat:
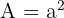
- Dreieck:
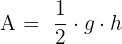
- Parallelogramm:
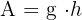
- Trapez:
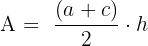
- Kreis:
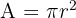
Dabei ist a = Länge und b = Breite.
Formeln zur Umfangsberechnung
Schauen wir uns nun die Formeln zur Berechnung des Umgangs an:
Rechteck: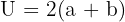
Quadrat: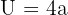
Kreis: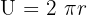
Lebst du in München und hast Interesse an Mathe Nachhilfe München?
Der Kreisumfang lässt sich auch mithilfe des Durchmessers berechnen: 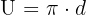
Formeln zur Volumenberechnung
Schließlich spielen noch die Formeln zur Berechnung von Volumen eine große Rolle:
- Quader:
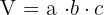
- Würfel:

- Zylinder:
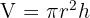
- Kegel:
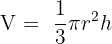
- Kugel:
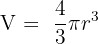
Entdecke die schönsten Mathe Zitate aus der Welt der Mathematik.
Satz des Pythagoras
Dieses Theorem aus dem Jahr 530 vor Christus ist wahrscheinlich einer der bekanntesten mathematischen Sätze und gehört noch heute zu den Grundpfeilern der modernen Mathematik.
In einem rechtwinkligen Dreieck ist die Summe der Katheten-Quadrate gleich dem Quadrat der Hypotenuse.
Der Satz des Pythagoras lautet also: 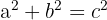
Die Umkehrung des Satzes versucht zu beweisen, dass ein Dreieck rechtwinklig ist: Wenn das Dreieck ABC ein Dreieck mit den Seiten a, b, c ist und die Beziehung so gilt, dann ist Dreieck ABC ein rechtwinkliges Dreieck mit [AB] als Hypotenuse.
Dieser Satz und seine Umkehrung haben die Geometrie revolutioniert.
Satz des Thales
Der Satz des Thales ist ein weiterer wichtiger Grundpfeiler der Mathematik und befasst sich mit dem 90°- Winkel eines Dreiecks.
Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C immer einen rechten Winkel.
Das zeigt, wie wichtig Mathematik im Alltag ist.
Konkret also: 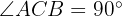
Die Umkehrung versucht zu beweisen, ob zwei Geraden parallel sind. So lassen sich Geraden und Parallelen bestimmen.
Logarithmus Formeln
Ein Logarithmus gibt an, zu welcher Potenz man eine Zahl b (Basis) erhöhen muss, um eine Zahl a zu erhalten. Es geht hier um Umkehrfunktionen und Exponentialfunktionen und es wird zwischen drei Systemen unterschieden:
natürliche Logarithmus
dekadische Logarithmus
binäre Logarithmus
Der Logarithmus folgt folgender Formel: 
Die Exponentialfunktion 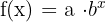

Eulersche Identität
Die Eulersche Identität verbindet die fünf wichtigsten mathematischen Konstanten in einer einzigen, eleganten Gleichung:
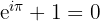
Dabei bedeuten die einzelnen Symbole folgendes:
- e = Eulersche Zahl (Basis des natürlichen Logarithmus, ≈2,718)
- i = imaginäre Einheit (i2=−1)
- π = Kreiszahl Pi (≈3,1416)
- Die ganzen Zahlen 0, neutrales Element in der Addition und 1, neutrales Element in der Multiplikation, sind in der Arithmetik und der Mathematik vertreten.
Formeln helfen dabei, Matherätsel zu lösen!
Potenzgesetze
Potenzgesetze helfen, Potenzen zu vereinfachen, zu multiplizieren oder zu dividieren. Sie gelten für beliebige Zahlen a≠0 und ganze Exponenten m,n.
Schauen wir uns die Potenzgesetze an:
- Multiplikation mit gleicher Basis:

- Division mit gleicher Basis:
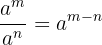
- Potenz einer Potenz:
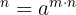
- Potenz eines Produkts:
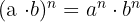
- Potenz eines Quotienten:
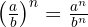
- Nullte Potenz:
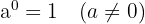
- Negative Exponenten:
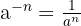
Vertiefe dein Wissen mit einer Mathe Nachhilfe!
Quadratische Gleichungen
Eine quadratische Gleichung hat die allgemeine Form: 
Die Lösung dieser Formel erfolgt mithilfe der sogenannten pq-Formel: 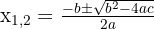
Hierbei gilt: 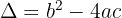
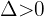 : zwei verschiedene reelle Lösungen
: zwei verschiedene reelle Lösungen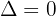 : eine doppelte Lösung
: eine doppelte Lösung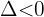 : zwei komplexe Lösungen
: zwei komplexe Lösungen
Eine quadratische Funktion  kann als Scheitelfunktion umgeschrieben werden als:
kann als Scheitelfunktion umgeschrieben werden als: 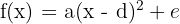
Falls die Gleichung lösbare Nullstellen x1,x2x1,x2 hat, kann sie geschrieben werden als: 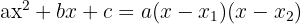
Dank komplexer Formel hilft Mathematik bei der Partnersuche.
Wurzelgesetze
Wurzeln helfen, Potenzen zu „entfernen“. Für positive Zahlen a,b≥0 und natürliche Zahlen m,n gelten die folgenden Regeln:
- Multiplikation unter der Wurzel:
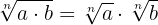
- Division unter der Wurzel:
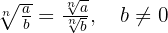
- Potenz einer Wurzel:
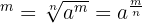
- Wurzel aus einer Potenz:
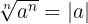 für gerade n
für gerade n - Wurzel aus einer Potenz:
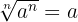 für ungerade n
für ungerade n
Ob einfach oder komplex, mit Mathematik Welt verstehen ist gar nicht so schwer.
Sinus und Kosinus
Sinus und Kosinus sind grundlegende trigonometrische Funktionen, die den Zusammenhang zwischen den Winkeln und den Seiten eines rechtwinkligen Dreiecks beschreiben.
Im rechtwinkligen Dreieck gilt: 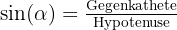
und 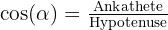
Dabei ist folgendes wichtig:
- Gegenkathete = Seite gegenüber dem Winkel

- Ankathete = Seite neben dem Winkel

- Hypotenuse = längste Seite des Dreiecks
Der Tangens wird mit der Formel angegeben: 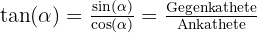
Lerne mathematische Formeln in der Mathe Nachhilfe Bochum.
Besondere mathematische Formeln
Einige mathematische Formeln finden sich auch in anderen Disziplinen wieder, etwa in der Physik. Hier gibt es einige Formeln, die jeder kennen sollte.
Gravitationsgesetz
Das Gravitationsgesetz von Isaac Newton besagt, dass jeder Körper auf jeden anderen Körper eine Anziehungskraft ausübt. Die Kraft ist proportional zu den Massen und umgekehrt proportional zum Quadrat des Abstands.
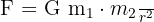
F ist die Kraft, G die Gravitationskonstante, mA und mB sind die Massepunkte der Körper A und B, r entspricht der Distanz in Metern.
Mit dieser Formel soll die Kraft, die ein Körper A auf einen Körper B auswirkt und umgekehrt, gezeigt werden.
Relativitätstheorie
Die Relativitätstheorie von Albert Einstein ist allseits bekannt, wenn auch nicht von allen verstanden. Sie besagt, dass Masse und Energie äquivalent sind. Lichtgeschwindigkeit ist konstant, Zeit und Raum können sich bei Bewegung relativ zueinander ändern.
Mit Mathe Nachhilfe online findest Du deine perfekte Lehrperson.
Die Relativitätstheorie lautet:
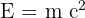
Diese Formel der Relativitätstheorie hat alle bis dahin bekannten physikalischen Gesetze revolutioniert. Sie ist heute noch von größter Bedeutung, denn Sie zeigt, dass sich Masse in Energie verwandeln kann und umgekehrt.
Chaostheorie
Mit der Chaostheorie beschreibt man Folgendes: Deterministische Systeme können aufgrund ihrer Abhängigkeit von Anfangsbedingungen (z. B. „Schmetterlingseffekt“) unvorhersehbar werden. Kleine Änderungen können also große, langfristige Effekte auslösen.
Dies wird mit einer mathematischen Näherungsformel angezeigt: 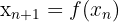
Ähnlich spannend ist die Wahrscheinlichkeitsrechnung beim Poker Spielen!
Mit KI zusammenfassen:















Kurz – knackig – prägnant und zeigt, was menschlicher Entdeckergeist ohne und mit Computer alles vermag. Und jeder dieser Entdecker steht auf den Wissensschultern seiner Vorgenerationen. Wie rasant Wissen die Umgebung des Menschen kulturschaffend beeinflusste, zeigen die immer kürzer werdenden Entdeckergeist Angaben. Einfach klasse.. und mit Beispielrechnungen a gefüttert. TOP!
Frage : wurde die relativitätstheorie schon mal mit der multiplikation von kreiszahl pi und der davon in potenz gesetzte eulersche konstante in relation gesetzt um damit die erweiterte beschreibung einer universalen formel von energieformen zu beschreiben ?
oder
meinung: die exponentielle fassung der relativitätstheorie einsteins durch diese zwei konstanten würde mir eine erklärung sein für die am rand beschleunigte expansion des unIversums oder sogar die eigenschaften dunkler energie und deren effekt auf den urknall hatte damit deren richtigkeit zurfolge ein organischer cluster einer sog. kugelsymmetrischen expandierender seifenblase sich, wenn so , ausbreitet . bis zum scheitelpunkt der Gaußschen verteilungsformel . dies würde den gnab gib einleuten und das all aus der expansion in die implusion führen.