Das Prinzip der Mathematik besteht darin, logische Gesetzmäßigkeiten systematisch aufzuzeigen. Die Zahl Pi, dargestellt durch den griechischen Buchstaben π, ist eine der wichtigsten Konstanten in der Mathematik. Sie wird aber auch in verwandten Fachbereichen wie der Physik und dem Ingenieurwesen genutzt. Sie wird auch als „Archimedes-Konstante“ oder „Ludolphsche Zahl“ bezeichnet.
Pi (π) ist eine mathematische Konstante, die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser beschreibt.
Der Zahlenwert von π ist irrational – das heißt, er lässt sich nicht als Bruch darstellen und nicht exakt berechnen.
Gerundet beginnt π mit 3,14159..., die Dezimalstellen setzen sich unendlich fort, ohne sich zu wiederholen.
🔍 Formel:
π = Umfang ÷ Durchmesser
Pi taucht überall dort auf, wo es um Kreise, Kugeln oder Wellen geht und ist eine der wichtigsten Zahlen der Mathematik und Physik.
Die Konstante fasziniert seit ihrer Entdeckung in der Antike mathematikbegeisterte Menschen und hat sogar ihren eigenen (inoffiziellen) Feiertag. Jedes Jahr am 14. März wird der Pi-Day gefeiert.
Was ist Pi? - Die Definition der Zahl π
Pi gehört zu den besonderen Zahlen der Mathematik. Der Buchstabe π wurde nicht zufällig als Symbol ausgewählt: Er steht ganz am Anfang der griechischen Wörter "περίμετρος" und „περιφέρεια“, die beide mit „Umfang“ übersetzt werden können. Und die Zahl Pi beschreibt das Verhältnis zwischen dem Umfang eines Kreises und seinem Durchmesser.
Ein Kreis definiert sich aus der Menge aller Punkte, die denselben Abstand zu einem bestimmten Punkt (Mittelpunkt des Kreises) aufweisen. Sie liegen so nah beieinander, dass sich daraus eine Linie ergibt. Die Länge dieser Kreislinie nennt man Umfang. Der Abstand der Kreislinie zum Mittelpunkt heißt Radius. Wenn wir ihn verdoppeln, erhalten wir den Durchmesser des Kreises.
Stell dir einen Kreis vor, wie zum Beispiel ein Pizzateller. Wenn du vom Rand des Kreises eine gerade Linie durch die Mitte bis zum genau gegenüberliegenden Rand ziehst, hast du den Durchmesser gefunden. Der Abstand von der Mitte bis zum Rand ist der Radius – und der Durchmesser ist einfach doppelt so lang wie der Radius.
Jetzt kommt das Spannende: Wenn du den Durchmesser misst und ihn mit einer Zahl multiplizierst, bekommst du den Umfang des Kreises – also die Länge einmal rundherum. Diese Zahl ist immer gleich, egal ob der Kreis klein wie eine Münze oder riesig wie ein Planet ist. Und genau diese Zahl nennt man Pi (π).
Das bedeutet: Der Umfang ist immer ein bisschen mehr als das Dreifache des Durchmessers – und wie viel genau, das sagt uns π.
Die Geschichte von Pi
Alte Papyrusrollen und Einschriften in Steinen lassen darauf schließen, dass dies bereits 2000 Jahre vor unserer Zeitrechnung den Ägyptern und Babyloniern bekannt war. Damals wurde mit einem ungefähren Wert von etwas mehr als 3 gerechnet. Die erste uns bekannte schriftliche Herleitung der Zahl Pi und ihrem Zahlenwert stammt aus der Zeit um 250 v. Chr. von dem griechischen Mathematiker Archimedes von Syrakus (ca. 287 v. Chr. bis 212 v. Chr.).1
Achtung Verwechslungsgefahr: Kennst du schon die goldenen Zahl Phi?
Die Annäherung an π durch Archimedes
Um den Wert von Pi zu berechnen, arbeitete Archimedes mit Vielecken, die er in und um einen Kreis mit dem Durchmesser 1 legte. In einem ersten Schritt berechnete er den Umfang eines regelmäßigen Sechsecks, dessen Eckpunkte genau auf der Kreislinie liegen.
Anschließend wiederholte er die Berechnung an einem 12-, einem 24-, einem 48- und schließlich einem 96-Eck. Im zweiten Schritt berechnete er nach derselben Vorgehensweise den Umfang von Vielecken, die außerhalb des Kreises liegen, ihn mit ihren Seiten aber berühren.
Liegen die Ecken eines Vielecks auf der Kreislinie, wird der Umfang des Vielecks immer etwas kleiner sein, als der des Kreises. Wenn sie außerhalb liegen, ist der berechnete Umfang hingegen etwas zu groß. Im Vergleich der Ergebnisse aus dem ersten und zweiten Schritt stellt man fest, dass sich die Werte immer weiter annähern, je mehr Ecken ein Vieleck hat. Bei 96-Ecken liegen die Seiten so nah aneinander, dass die Differenz nur noch minimal ist.
Berechnet man nun das Verhältnis von Umfang und Durchmesser eines Vielecks außerhalb und eines innerhalb desselben Kreises, erhält man eine Ober- und eine Untergrenze für Pi. Archimedes konnte so den Wert von Pi bereits auf zwei Nachkommastellen genau eingrenzen (3,1408 < π < 3,1429).
Wir haben deine Neugier geweckt? Lies dir auch unseren Artikel über die imaginäre Zahl i durch.
Moderne Entwicklungen – von Van Ceulen bis Chudnovsky
Archimedes Methode wurde in der Folge von zahlreichen Mathematikern aufgegriffen und fortgeführt. Im 17. Jahrhundert gelang es Ludolph van Ceulens, sich Pi auf 35 Stellen anzunähern. Rund hundert Jahre später fand John Machin eine Formel, mit der er bereits 100 Stellen errechnen konnte. Die seither mit viel Ehrgeiz betriebene Rekordjagd nahm mit dem Aufkommen von Rechenmaschinen im 20. Jahrhundert ganz neue Dimensionen an.
ca. 1900–1650 v. Chr.
Babylonier & Ägypter
Babylonier & Ägypter nutzen π ≈ 3,125 und 3,1605
ca. 250 v. Chr.
Archimedes
Archimedes beschreibt π erstmals genau mit dem Polygon-Verfahren
5. Jh. n. Chr.
Chinesische Mathematiker
Chinesische Mathematiker wie Zu Chongzhi erreichen π ≈ 355/113
17. Jh.
Van Ceulen
Van Ceulen: ca. 35 Dezimalstellen; Machin: ca. 100 Stellen
20.–21. Jh.
Digitale Berechnungen
Digitale Berechnungen wachsen exponentiell – bis zu 300 Trillionen Dezimalstellen im April 2025
Aus hunderten Nachkommastellen wurden Tausende und 1989 gelang es dem amerikanischen Mathematiker David Chudnovsky, als Erster die Millionengrenze zu knacken. Heute sind nicht weniger als 300 Trillionen Nachkommastellen von Pi bekannt (Stand: 16.05.2025)2. Die Suche nach weiteren Stellen wird wohl noch ewig weitergehen; denn Pi ist unendlich.
Für die praktische Anwendung ist eine solch enorme Genauigkeit natürlich weder tauglich noch nötig. Aus diesem Grund nutzen wir weiterhin eine Annäherung an Pi, die sich auf einige wenige Nachkommastellen beschränkt. In der Schule lernst du wahrscheinlich mit dem Wert 3,1416 zu rechnen und erhältst damit schon recht genaue Ergebnisse.
Bereits im Jahr 1881 zeigte der Astronom Simon Newcomb, dass 10 Dezimalstellen von Pi vollständig ausreichen, um den Umfang der Erde zu berechnen. Für die Ermittlung des Umfangs des ganzen sichtbaren Universums reichen laut Newcomb 30 Stellen aus.3
Als Bruch wird die Zahl Pi übrigens so geschrieben: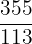 
.
Das Ergebnis ist immerhin auf 6 Nachkommastellen genau. Diese Rechnungsweise wurde verwendet, bevor es eine π-Taste auf Taschenrechnern gab. Die Darstellung von Pi als Bruch ist eine starke Vereinfachung, die genau genommen falsch ist. Warum, schauen wir uns als Nächstes an.
Möchtest du mehr über die Kreiszahl Pi erfahren? In der Mathe Nachhilfe Bochum wird dir alles genau erklärt.
Warum Pi eine ganz besondere Zahl ist
Die Kreiszahl π ist nicht nur irgendeine mathematische Konstante – sie ist ein echtes Phänomen. Seit Jahrtausenden fasziniert sie Mathematiker, weil sie sich jeder einfachen Darstellung entzieht. Man kann sie nicht exakt als Bruch schreiben, nicht vollständig berechnen und auch nicht mit Lineal und Zirkel konstruieren. Doch was genau macht π so besonders?
π ist irrational – was bedeutet das?
In der Mathematik unterscheidet man rationale und irrationale Zahlen.
- Rationale Zahlen kann man als Bruch schreiben, zum Beispiel ½ oder 7/4. Ihre Dezimalzahlen enden entweder irgendwann oder sie wiederholen sich in einem festen Muster (z. B. 0,333… oder 2,145145145…).
- Irrationale Zahlen dagegen kann man nicht als Bruch schreiben. Ihre Nachkommastellen sind unendlich lang und nicht periodisch – sie wiederholen sich also nie und folgen keinem erkennbaren Muster. Neben π gehören auch √2 oder die Eulersche Zahl e zu dieser Gruppe.
Dass π irrational ist, wurde lange vermutet, aber erst 1770 von Johann Heinrich Lambert bewiesen. Er nutzte dazu eine sogenannte Kettenbruchdarstellung der Tangensfunktion – eine clevere, aber komplizierte Methode, die endgültig zeigte: π ist unendlich, nicht vorhersehbar und niemals als Bruch darstellbar.
Ist Pi algebraisch?
Irrationale Zahlen sind nicht alle gleich, auch sie lassen sich weiter unterscheiden. Man unterscheidet:
- Algebraische irrationale Zahlen, wie z. B. √2. Diese lassen sich als Lösungen von ganzzahligen Polynomen darstellen. Beispiel: √2 ist eine Lösung der Gleichung
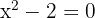. - Transzendente Zahlen, wie π, gehen noch einen Schritt weiter. Sie lassen sich nicht als Polynom beschreiben. Vereinfacht gesagt heißt das, dass eine transzendente Zahl wie π durch endlich viele algebraische Manipulationen niemals den Wert 0 erreichen kann.
Wenn du mehr über die Zahl Null erfahren möchtest, bist du bei uns genau richtig.
Die Transzendenz von π wurde erst 1882 vom deutschen Mathematiker Ferdinand von Lindemann bewiesen – ein weiterer Meilenstein in der Geschichte dieser besonderen Zahl.4
Transzendente Zahlen hingegen lassen sich nicht als Polynom beschreiben. Vereinfacht gesagt heißt das, dass eine transzendente Zahl wie π durch endlich viele algebraische Manipulationen niemals den Wert 0 erreichen kann.
Warum kann man den Kreis nicht quadrieren?
Aufgrund seiner Transzendenz ist Pi auch nicht konstruierbar. Das bedeutet, man kann die Zahl nicht allein mit einem Lineal und einem Zirkel konstruieren. Dadurch ist es auch nicht möglich, mit genannten Hilfsmitteln, ein Quadrat zu zeichnen, das exakt dieselbe Fläche wie ein gegebener Kreis hat.
Diese berühmte „Quadratur des Kreises“ beschäftigte Mathematiker über viele Jahrhunderte – bis der Beweis der Transzendenz endgültig zeigte: Es geht einfach nicht.
Wofür wird die Kreiszahl Pi verwendet?
Die Kreiszahl Pi ist keineswegs dazu da, Schüler*innen sinnlos zu quälen. Sie zu kennen und mit ihr umgehen zu können, gehört zur mathematischen Allgemeinbildung. Schauen wir uns also einmal an, wann und wie Pi genau zur Anwendung kommt.
Formeln mit Pi
Die Kreiszahl π wird in verschiedenen Formeln verwendet, die du vielleicht schon aus dem Unterricht kennst:
- Kreisumfang:
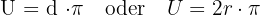
- Kreisfläche:
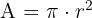
- Kugeloberfläche:
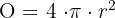
- Kugelvolumen:
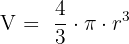
Mit diesen Formeln lassen sich nicht nur Kreise beschreiben, sondern auch viele Körper aus dem Alltag – etwa Zylinder, Kugeln oder Kegel.
Du brauchst Statistik Nachhilfe? Entdecke das Angebot von Superprof und finde den perfekt auf dich zugeschnittenen Kurs.
Anwendungsbeispiele: So hilft dir Pi im Alltag
Die Berechnung der Fläche oder des Umfangs eines Kreises wird dir beispielsweise auch weiterhelfen, wenn du das Volumen oder die Oberfläche eines Zylinders oder Kegels berechnen sollst. Aber wozu braucht man das alles? Folgende zwei Textaufgaben zeigen dir Beispiele, in denen die Kreiszahl Pi dabei helfen kann, praktische Probleme zu lösen:
Durchmesser eines Baumstamms berechnen
Aufgabe: Ein Förster möchte den Durchmesser eines Baumstamms errechnen. Dazu misst er seinen Umfang mit einem Maßband. Der Umfang beträgt 89 cm. Wie groß ist der Durchmesser?
Lösung: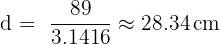 
Antwort: Der Durchmesser des Stammes beträgt ca. 28,34 cm.
Reifenumdrehungen auf 1 km Strecke
Aufgabe: Ein Autobesitzer möchte besser abschätzen können, wie sehr sich seine Autoreifen abnutzen werden. Dazu muss er wissen, wie oft sich ein Rad auf einer Strecke von 1 Km dreht. Der Durchmesser eines Reifens misst 75,2 cm.
Lösung:
Zuerst den Umfang berechnen: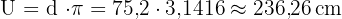 
1 km = 100.000 cm
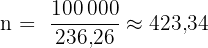
Antwort: Das Rad dreht sich etwa 423-mal auf 1 km.
Brauchst du Nachhilfe Mathe?
Pi und das Bogenmaß: Wenn Grad nicht ausreichen
Ein weiterer Bereich, in dem uns π oft begegnet, ist die Trigonometrie, die sich mit dem Verhältnis der Seiten und Winkel von Dreiecken beschäftigt. Die Größe eines Winkels kann entweder im Gradmaß oder im Bogenmaß angegeben werden.
Das Bogenmaß hat den sogenannten Einheitskreis mit dem Radius 1 zur Grundlage. Wenn wir vom Mittelpunkt aus zwei Geraden bis zur Kreislinie ziehen, wird die Länge jeder dieser Geraden dem Radius entsprechen. Das Bogenmaß ist nun der Abschnitt der Kreislinie zwischen den beiden Punkten, an denen die Geraden die Linie berühren.
Je größer der Winkel zwischen den beiden Geraden ist, umso länger wird auch das Bogenmaß. Das bedeutet, dass es zu jedem Gradmaß ein entsprechendes Bogenmaß gibt. Liegen beispielweise die beiden Geraden direkt übereinander, haben wir einen Winkel von 360° und das Bogenmaß entspricht dem Umfang des Kreises, also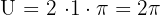 
.
Zeichnen wir nun einen rechten Winkel (α = 90°) ein, beträgt das Bogenmaß nur noch einen Viertel des Umfangs des Einheitskreises. Die Formel, die zur Berechnung verwendet wird, lautet: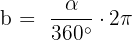 
. Das bedeutet in unserem Beispiel 
.
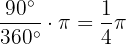Wenn du also dachtest, Pi sei nur eine nervige Zahl aus dem Mathebuch – weit gefehlt! Von Holzrädern über Baumstämme bis zu Planetensystemen: Die Kreiszahl begleitet dich durch die ganze Welt.
Kreiszahl Pi: Unendliche Stellen, unendliche Faszination
Neben dem praktischen Nutzen, übt die Konstante Pi, genau wie die perfekte Zahl oder auch "vollkommene Zahl" seit langer Zeit eine große Faszination auf Menschen aus. Nicht nur das Entdecken möglichst vieler Nachkommastellen, sondern auch das Auswendiglernen davon spornt Pi-Fans zu gedanklichen Höchstleistungen an.
Der britische „Savant“ (Person mit Inselbegabung) rezitierte 2004 erwiesenermaßen 22.514 Dezimalstellen. Übertroffen wurde diese Leistung 2005 von Lu Chao (67.890 Dezimalstellen) und 2015 von Rajveer Meena, der es mit 70.000 Nachkommastellen ins Guinness-Buch der Rekorde schaffte.5 Immer wieder gibt es Menschen, die behaupteten, noch weit mehr Stellen zu kennen, was aber (bisher) nicht offiziell bestätigt werden konnte.
Wenn du es auf immerhin schon beachtliche 24 Stellen bringen möchtest, kann dir folgender Merkspruch weiterhelfen:
Wie, o dies π macht ernstlich so vielen viele Müh, Lernt immerhin, Jünglinge, leichte Verselein, wie so zum Beispiel dies dürfte zu merken sein!
Die Anzahl Buchstaben pro Wort entspricht dabei der Zahl, die du dir merken musst: π = 3,14159265358979323846264.
In der Mathe Nachhilfe online kannst du alles über die Zahl Pi und ihre Anwendungsbereiche erfahren.
Die Unendlichkeit und Irrationalität von Pi laden aber noch zu vielen weiteren Gedankenspielen ein. Falls π eine sogenannt normale Zahl ist (was bisher noch nicht bewiesen werden konnte), kommt darin jeder mögliche Ziffernblock vor und Ziffernblöcke gleicher Länge gleich häufig auftreten. Das würde bedeuten, dass jede erdenkliche Zahlenkombination darin enthalten wäre.
Wenn man jetzt den Zahlenkombinationen Buchstaben zuordnet würde, wäre jeder jemals geschriebene Text, ob von dir oder von Shakespeare, irgendwo in π enthalten. Dasselbe gilt natürlich auch für deine Telefonnummer und meine Sozialversicherungsnummer.
Faszinierend ist auch, dass sich π durch ein Wahrscheinlichkeitsexperiment berechnen lässt. Herausgefunden hat dies der Graf de Buffon im 18. Jahrhundert. Wenn man längliche Objekte (wie z.B. Nadeln oder Streichhölzer) zufällig auf einen Untergrund mit Gittermuster wirft und zählt, wie viele der Objekte eine Linie kreuzen, erhält man eine Annäherung an Pi.
Sind die Abstände zwischen den Linien gleich lang, wie die geworfenen Objekte, rechnet man: 2x Anzahl geworfener Stäbe geteilt durch Anzahl der Stäbe, die die Linie kreuzen. Je mehr Objekte man wirft, umso mehr Nachkommastellen von π wird man erhalten. Bekannt ist diese Formel auch als das Buffonsche Nadelproblem.
Hast du noch nicht genug? Dann schau dir auch unseren Artikel zu den Primzahlen an.
Referenzen
- Exploratorium, "A Brief History of Pi (π)" https://www.exploratorium.edu/pi/history-of-pi
- Numberworld https://www.numberworld.org/y-cruncher/news/2025.html#2025_5_16
- Zitiert in D MacHale, Comic Sections (Dublin 1993)
- Lindemann, F. (1882), "Über die Zahl π.", Mathematische Annalen, 20 (2): 213–225
- Guinnes Buch der Rekorde https://www.guinnessworldrecords.com/world-records/most-pi-places-memorised
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
Interessanter Artikel, aber das Gendern nervt ungemein. Wer immer noch nicht das generische Maskulinum und den Unterschied zwischen biologischem und grammatikalischem Geschlecht verstanden hat, muss zwar keine Mathe, aber auf jeden Fall Deutsch wiederholen.
Die unendliche Zahl von Pi könnte bedeuten das unendliche Universum, da nach Einstein das Universum rund ist.