Ein Datensatz aus 
Zahlen, dessen Mittelwert 
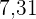ist, wird mit den Zahlen 
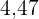und 
addiert. Wie lautet der Mittelwert des neuen Datensatzes?
Der Mittelwert des Datensatzes aus Zahlen ist
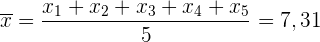
Somit
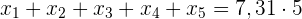
Der Mittelwert aus den 
Zahlen ist
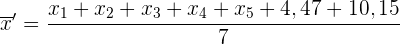
Das ist dasselbe wie
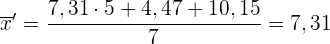
Ein Zahnarzt beobachtet, wie oft Karies bei jedem von 
Kindern einer bestimmte Schule vorkommt. Die erhaltenen Informationen sind in der folgenden Tabelle dargestellt:
| Anzahl Karies | fi | ni |
|---|---|---|
| 0 | 25 | 0,25 |
| 1 | 20 | 0,20 |
| 2 | x | z |
| 3 | 15 | 0,15 |
| 4 | y | 0,05 |
- Vervollständige die Tabelle, indem du die Werte für
, 
, 
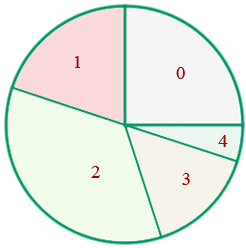
ermittelst. - Erstelle ein Kreisdiagramm.
- Berechne die durschnittliche Anzahl von Karies.
aTabelle
Die Summe der relativen Häufigkeiten muss 
sein:
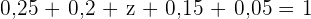
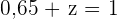
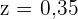
Die relative Häufigkeit eines Datenwerts ist gleich seiner absoluten Häufigkeit geteilt durch . Dies ist die Summe der absoluten Häufigkeiten.
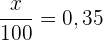
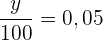
| Anzahl Karies (xi) | fi | ni | fi • ni |
|---|---|---|---|
| 0 | 25 | 0,25 | 0 |
| 1 | 20 | 0,20 | 20 |
| 2 | 35 | 0,35 | 70 |
| 3 | 15 | 0,15 | 45 |
| 4 | 5 | 0,05 | 20 |
| 100 | 155 |
bKreisdiagramm
Wir berechnen die Grade, die einer Einheit der absoluten Häufigkeit entsprechen
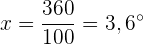
Wir berechnen die Grade, die jeder absoluten Häufigkeit entsprechen.
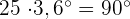
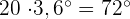
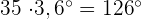
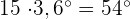
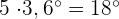
cArithmetisches Mittel
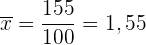
Wir haben einen Datensatz aus 
Daten:
Ermittle den Median und die Quartile.
1 Wir ordnen die Daten
Als Erstes ordnen wir die Daten in aufsteigender Reihenfolge:
2 Median
Da wir eine gerade Anzahl von Daten haben, ist der Median der Mittelwert der zentralen Werte:
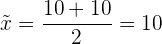
3 Quartile
Um das erste Quartil zu erhalten, dividieren wir die Anzahl der Daten durch 
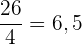
Wir sehen uns an, wo die Werte 
und liegen und nehmen den Durchschnitt
Das zweite Quartil ist der Median
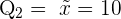
Um das dritte Quartil zu bestimmen, multiplizieren wir die Anzahl der Daten mit 
und dividieren durch
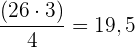
Wir sehen uns an, wo die Werte 
und 
liegen und nehmen den Durchschnitt
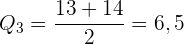
Ein Kinderarzt erstellt folgende Tabelle über das Alter von Kindern, in dem sie ihre ersten Schritte machen:
| Monate | Kinder |
|---|---|
| 9 | 1 |
| 10 | 4 |
| 11 | 9 |
| 12 | 16 |
| 13 | 11 |
| 14 | 8 |
| 15 | 1 |
- Zeichne die Normalverteilungskurve
- Berechne Modus, Median, Mittelwert und Varianz
1 Normalverteilungskurve
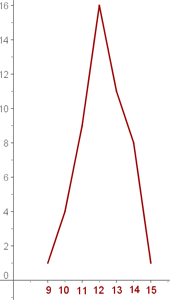
2 Tabelle vervollständigen
Wir vervollständigen die Tabelle mit folgenden Daten:
Kumulierte Häufigkeit 
, um den Median zu berechnen.
Das Produkt aus der Variable und ihrer absoluten Häufigkeit 
, um den Mittelwert zu berechnen.
Das Produkt aus der Variable zum Quadrat und ihrer absoluten Häufigkeit 
, um die Varianz und die Standardabweichung zu berechnen.
| xi | fi | Fi | xi • fi | xi2 • fi |
|---|---|---|---|---|
| 9 | 1 | 1 | 9 | 81 |
| 10 | 4 | 5 | 40 | 400 |
| 11 | 9 | 14 | 99 | 1089 |
| 12 | 16 | 30 | 192 | 2304 |
| 13 | 11 | 41 | 143 | 1859 |
| 14 | 8 | 49 | 112 | 1568 |
| 15 | 1 | 50 | 15 | 225 |
| 50 | 610 | 7526 |
3
Der Modus ist der Wert mit der höchsten absoluten Häufigkeit
Betrachtet man die Spalte 
, so entspricht die höchste absolute Häufigkeit 
dem Wert 
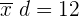
4 Median
Um den Median zu berechnen, dividieren wir 
durch 
. Wir sehen, dass die Zelle 
, in der sich 
befindet, entspricht
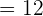
5 Arithmetisches Mittel
Wir berechnen das Ergebnis aus dem Produkt aus der Variablen und ihrer absoluten Häufigkeit 
, die 
ist, und dividieren sie durch 
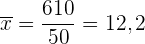
6 Varianz
Wir berechnen das Ergebnis aus 
, dividieren es durch und subtrahieren vom Ergebnis das arithmetische Mittel zum Quadrat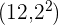 
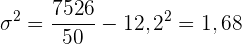
Vervollständige folgende statistische Tabelle mit den fehlenden Daten:
| xi | fi | Fi | ni |
|---|---|---|---|
| 1 | 4 | 0,08 | |
| 2 | 4 | ||
| 3 | 16 | 0,16 | |
| 4 | 7 | 0,14 | |
| 5 | 5 | 28 | |
| 6 | 38 | ||
| 7 | 7 | 45 | |
| 8 |
Berechne Mittelwert, Median und Modus dieser Verteilung.
1 Tabelle
-
-
Zeile 1
-
Die erste kumulierte Häufigkeit fällt mit der ersten absoluten Häufigkeit zusammen
Die erste kumulierte relative Häufigkeit 
entspricht der ersten absoluten Häufigkeit 
geteilt durch 
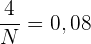
Somit ist 
die Gesamtzahl der Daten
-
-
Zeile 2
-
Die zweite kumulierte Häufigkeit entspricht der vorhergehenden kumulierten Häufigkeit plus die entsprechende absolute Häufigkeit
Die kumulierte relative Häufigkeit 
entspricht der absoluten Häufigkeit geteilt durch
-
-
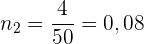
Zeile 3
-
Um die absolute Häufigkeit zu bestimmen, gibt es zwei Möglichkeiten
1. Mittels der kumulierten relativen Häufigkeit:
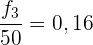
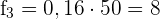
2. Die absolute Häufigkeit ist die Differenz aus 
und 
-
-
Zeile 4
-
Die kumulierte Häufigkeit entspricht der vorhergehenden kumulierten Häufigkeit plus die entsprechende absolute Häufigkeit 
-
-
Zeile 5
-
Die kumulierte relative Häufigkeit 
entspricht der absoluten Häufigkeit 
geteilt durch
-
-
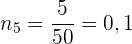
Zeile 6
-
Analog zu Zeile drei haben wir zwei Möglichkeiten
Die absolute Häufigkeit enspricht der kumulierten Häufigkeit 
minus die vorhergehende kumulierte Häufigkeit 
. Das heißt, der Differenz aus 
und 
Die kumulierte relative Häufigkeit 
entspricht der absoluten Häufigkeit 
geteilt durch
-
-
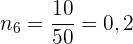
Zeile 7
-
Die kumulierte relative Häufigkeit 
entspricht der absoluten Häufigkeit geteilt durch
-
-
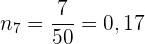
Zeile 8
-
Die letzte kumulierte Häufigkeit entspricht
Die absolute Häufigkeit entspricht der kumulierten Häufigkeit 
minus die vorhergehende kumulierte Häufigkeit 
. Das heißt, der Differenz aus 
und 
Die kumulierte relative Häufigkeit 
entspricht der absoluten Häufigkeit geteilt durch
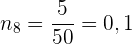
2 Tabelle vervollständigen
Mit den erhaltenen Daten können wir die Tabelle vervollständigen. Außerdem ergänzen wir die Tabelle um die Spalte des Produkts aus Variable und absoluter Häufigkeit, um den Mittelwert zu berechnen
| xi | fi | Fi | ni | xi • fi |
|---|---|---|---|---|
| 1 | 4 | 4 | 0,08 | 4 |
| 2 | 4 | 8 | 0,08 | 8 |
| 3 | 8 | 16 | 0,16 | 24 |
| 4 | 7 | 23 | 0,14 | 28 |
| 5 | 5 | 28 | 0,10 | 25 |
| 6 | 10 | 38 | 0,20 | 60 |
| 7 | 7 | 45 | 0,14 | 49 |
| 8 | 5 | 50 | 0,10 | 40 |
| 50 | 238 |
3 Arithmetisches Mittel
Wir berechnen die Summe aus Variable und absoluter Häufigkeit 
, die 
ist, und teilen sie durch
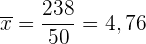
4 Median
Um den Median zu berechnen, dividieren wir durch . Wir stellen fest, dass die Zelle , in der sich befindet, entspricht
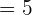
5 Modus
Der Modus ist der Wert mit der höchsten absoluten Häufigkeit
Die Spalte zeigt, dass die höchste absolute Häufigkeit der Zahl entspricht
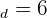
Sieh dir folgende Daten an: 
. Aufgabe:
- Berechne Mittelwert und Varianz.
- Wenn wir alle oben genannten Daten mit 3 multiplizieren, wie lauten dann der neue Mittelwert und die neue Varianz?
a Mittelwert
Wir ordnen die Daten
.
Wir addieren die Werte und dividieren durch die Gesamtzahl der Daten.
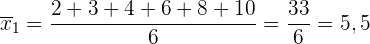
2 Varianz
Wir nehmen den Durchschnitt der Zahlen zum Quadrat und subtrahieren den Mittelwert zum Quadrat.
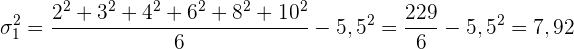
Mit multipliziert...
1 Mittelwert
Wenn wir alle Werte der Variablen mit multiplizieren, wird das arithmetische Mittel mit multipliziert
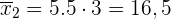
b Varianz
Wenn wir alle Werte der Variablen mit multiplizieren, wird die Varianz mit zum Quadrat multipliziert
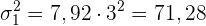
Das Ergebnis, das man erhält, wenn zwei Würfel 
Mal geworfen werden, ist in folgender Tabelle gegeben:
| Ergebnis | Male, die Würfel geworfen wurden |
|---|---|
| 2 | 3 |
| 3 | 8 |
| 4 | 9 |
| 5 | 11 |
| 6 | 20 |
| 7 | 19 |
| 8 | 16 |
| 9 | 13 |
| 10 | 11 |
| 11 | 6 |
| 12 | 4 |
- Berechne Mittelwert und Standardabweichung.
- Ermittle den Prozentsatz der Werte innerhalb des Intervalls
.
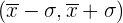1 Tabelle vervollständigen
Wir vervollständigen die Tabelle mit:
Dem Produkt aus Variable und absoluter Häufigkeit , um den Mittelwert zu berechnen.
Dem Produkt aus Variable zum Quadrat und absoluter Häufigkeit , um die Standardabweichung zu berechnen.
| xi | fi | xi • fi | xi2 • fi |
|---|---|---|---|
| 2 | 3 | 6 | 12 |
| 3 | 8 | 24 | 72 |
| 4 | 9 | 36 | 144 |
| 5 | 11 | 55 | 275 |
| 6 | 20 | 120 | 720 |
| 7 | 19 | 133 | 931 |
| 8 | 16 | 128 | 1024 |
| 9 | 13 | 117 | 1053 |
| 10 | 11 | 110 | 1100 |
| 11 | 6 | 66 | 726 |
| 12 | 14 | 48 | 576 |
| 120 | 843 | 6633 |
2 Arithmetisches Mittel
Wir haben die Tabelle um die Spalte 
erweitert, da wir die Summe 
erhalten möchten. Diese dividieren wir dann durch 
, um den Mittelwert zu erhalten
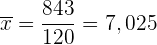
3 Standardabweichung
Wir haben die Tabelle um die Spalte erweitert, da wir die Summe 
erhalten möchten. Diese dividieren wir durch 
und subtrahieren vom Ergebnis das arithmetische Mittel zum Quadrat 
. Schließlich ziehen wir noch die Wurzel
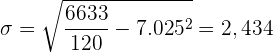
4 Prozentsatz
Da wir die Standardabweichung kennen, können wir das genannte Intervall berechnen.
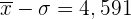
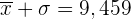
Die Werte innerhalb des Intervalls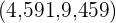 
sind diejenigen, die den Summen von 
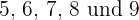entsprechen. Wir addieren die absoluten Häufigkeiten.
Mittels der folgenden Verteilung bestimmen wir den Prozentsatz:
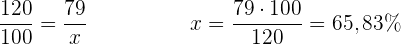
Die Körpergröße der Spieler einer Basketballmannschaft ist in der Tabelle angegeben:
| Größe | Anzahl der Spieler |
|---|---|
| [170, 175) | 1 |
| [175, 180) | 3 |
| [180, 185) | 4 |
| [185, 190) | 8 |
| [190, 195) | 5 |
| [195, 200) | 2 |
Berechne:
- Mittelwert.
- Median.
- Standardabweichung.
- Wie viele Spieler liegen über dem Mittelwert plus Standardabweichung?
1 Tabelle vervollständigen
Wir vervollständigen die Tabelle mit:
Der kumulierten Häufigkeit , um den Median zu berechnen
Dem Produkt aus Variable und absoluter Häufigkeit , um den Mittelwert zu berechnen
Dem Produkt aus Variable zum Quadrat und absoluter Häufigkeit 
, um die Varianz und die Standardabweichung zu berechnen
| xi | fi | Fi | xi • fi | xi 2 • i | |
|---|---|---|---|---|---|
| [1.70, 1.75) | 1,725 | 1 | 1 | 1,725 | 2,976 |
| [1.75, 1.80) | 1,775 | 3 | 4 | 5,325 | 9,453 |
| [1.80, 1.85) | 1,825 | 4 | 8 | 7,300 | 13,324 |
| [1.85, 1.90) | 1,875 | 8 | 16 | 15 | 28,128 |
| [1.90, 1.95) | 1,925 | 5 | 21 | 9,625 | 8,53 |
| [1.95, 2.00) | 1,975 | 2 | 23 | 3,95 | 7,802 |
| 23 | 42,925 | 80,213 |
2 Mittelwert
Wir berechnen das Ergebnis aus Variable mal absolute Häufigkeit , das 
ist und teilen durch 
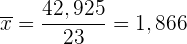
3 Median
Wir suchen das Intervall, in dem der Median liegt. Hierzu dividieren wir durch , da der Median der Zentralwert ist
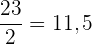
Wir suchen in der Spalte der kumulierten Häufigkeiten das Intervall, das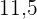 
enthält
Wir wenden die Formel zur Berechnung des Medians für gruppierte Daten an und extrahieren folgende Daten:
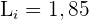
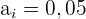
Der Median ist
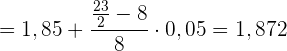
4 Standardabweichung
Wir berechnen das Ergebnis aus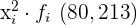 
, dividieren durch 
und subtrahieren das arithmetische Mittel zum Quadrat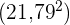 
. Schließlich ziehen wir die Wurzel
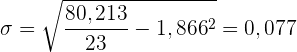
Somit
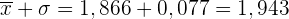
Dieser Wert gehört zu einem Perzentil, das im vorletzten Intervall liegt.
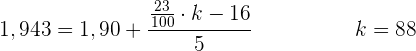
Wir ermitteln folgendes Verhältnis:
Es gibt nur 3 Spieler, die über 
liegen
Ein Würfel wird 200 Mal geworfen. Die Ergebnisse sind in der folgenden Tabelle dargestellt:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| fi | a | 32 | 35 | 33 | b | 35 |
Bestimme
und 
, wenn bekannt ist, dass der Durchschnittswer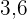t 
ist.1 Vervollständige die Tabelle
Wir ermitteln das Ergebnis aus und
| xi | fi | xi • fi |
|---|---|---|
| 1 | a | a |
| 2 | 32 | 64 |
| 3 | 35 | 125 |
| 4 | 33 | 132 |
| 5 | b | 5b |
| 6 | 35 | 210 |
| 135+a+b | 511+a+5b |
2 Gleichungen aufstellen
Die Summe der absoluten Häufigkeiten enspricht 
Daraus können wir schließen, dass
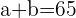
Die Summe aus geteilt durch 
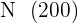ist der Mittelwert
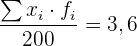
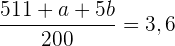
Daraus können wir schließen, dass
3 Wir lösen das Gleichungssystem
Schließlich
Wir sehen uns folgendes Histogramm an. Dieses stellt die Gewichtsverteilung unter Gymnasiasten dar:
-
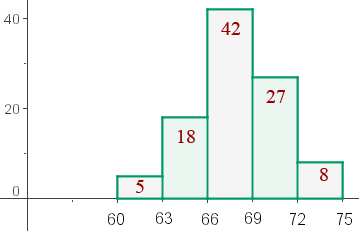
- Erstelle die Verteilungstabelle.
-
- Wenn Andreas
kg wiegt, wieviele Schüler wiegen weniger als er?
- Wenn Andreas
-
- Berechne den Modus.
-
- Bestimme den Median.
- Ab welchen Werten sind die
der schwersten Schüler einzuordnen?
1 Verteilungstabelle
| xi | fi | Fi | |
|---|---|---|---|
| [60,63) | 61,5 | 5 | 5 |
| [63, 66) | 64,5 | 18 | 23 |
| [66, 69) | 67,5 | 42 | 65 |
| [69, 72) | 70,5 | 27 | 92 |
| [72, 75) | 73,5 | 8 | 100 |
| 100 |
2 Schüler, die weniger als Andreas wiegen
Wir sehen, dass die ersten vier Intervalle die Schüler enthalten, die weniger wiegen als Andreas. Wir addieren die absoluten Häufigkeiten 
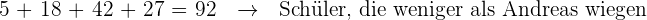
3 Modus
Als Erstes suchen wir das Intervall, in dem der Modus liegt. Also das Intervall mit der höchsten absoluten Häufigkeit
Die Modalklasse ist: 
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren folgende Daten:
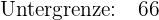
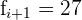
Somit ist der Modus
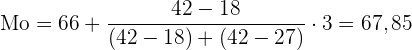
4 Median
Wir suchen das Intervall, in dem der Median liegt. Dazu dividieren wir durch , da der Median der Zentralwert ist
Wir suchen in der Spalte der kumulierten Häufigkeiten das Intervall, das enthält
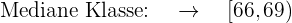
Wir wenden die Formel zur Berechnund des Medians für gruppierte Daten an und extrahieren folgende Daten:
Wir berechnen somit den Median
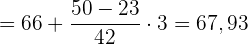
5 Drittes Quartil
Der Wert oberhalb dessen sich der Schüler, die mehr wiegen, befinden, ist das dritte Quartil.
Wir suchen das Intervall, in dem sich das dritte Quartil befindet. Wir multiplizieren mit 
und dividieren durch
Wir suchen in der Spalte der kumulierten Häufigkeiten das Intervall, das 
enthält
Die Klasse von 
ist: 
Wir wenden die Formel zur Berechnung von Quartilen für gruppierte Daten an und extrahieren folgende Daten:
Somit ist das dritte Quartil
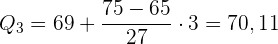
Berechne aus dieser Verteilung der kumulierten absoluten Häufigkeiten:
| Alter | Fi |
|---|---|
| [0,2) | 4 |
| [2,4) | 11 |
| [4,6) | 24 |
| [6,8) | 34 |
| [8,10) | 40 |
- Arithmetisches Mittel und Standardabweichung.
- Zwischen welchen Werten liegen die 10 mittleren Altersstufen?
- Stelle die Normalverteilungskurve von kumulierten absoluten Häufigkeiten dar.
1 Tabelle vervollständigen
Wir erweitern die Tabelle um eine Spalte mit den absoluten Häufigkeiten
Die erste absolute Häufigkeit stimmt mit der ersten kumulierten Häufigkeit überein. Um die folgenden Häufigkeiten zu berechnen, müssen wir die vorherige absolute Häufigkeit von der folgenden absoluten Häufigkeit subtrahieren
| xi | fi | Fi | xi • fi | xi2 • fi | |
|---|---|---|---|---|---|
| [0,2) | 1 | 4 | 4 | 4 | 4 |
| [2,4) | 3 | 7 | 11 | 21 | 63 |
| [4,6) | 5 | 13 | 24 | 65 | 325 |
| [6,8) | 7 | 10 | 34 | 70 | 490 |
| [8,10) | 9 | 6 | 40 | 54 | 486 |
| 40 | 214 | 1368 |
2 Mittelwert
Wir haben die Tabelle um die Spalte erweitert, da wir das Ergebnis 
ermitteln möchten. Dieses dividieren wir dann durch 
, um den Mittelwert zu erhalten
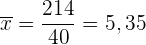
3 Standardabweichung
Wir haben die Tabelle um die Spalte 
erweitert, da wir das Ergebnis 
ermitteln möchten. Dieses dividieren wir dann durch 
und subtrahieren vom Ergebnis das arithmetische Mittel zum Quadrat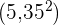 
. Zum Schluss ziehen wir die Wurzel
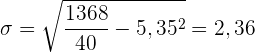
4 Zentrales Alter
Sehen wir uns nun an, welchen Prozentsatz die 
Altersstufen ausmachen
Die Schüler repräsentieren die zentralen der Verteilung.
Wir müssen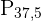 
und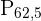 
bestimmen.
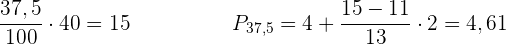
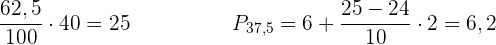
Die zentralen Altersstufen liegen im Intervall: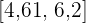 
.
5 Normalverteilungskurve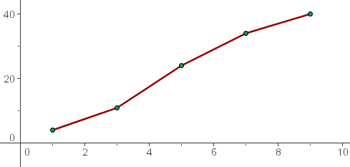
Eine Person 
ist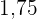 
m groß und lebt in einer Stadt, in der die Durchschnittsgröße 
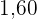m beträgt. Die Standardabweichung liegt bei cm. Eine andere Person 
ist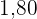 
m groß und lebt in einer Stadt, in der die Durchschnittsgröße 
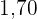m beträgt. Die Standardabweichung liegt bei 
cm. Welche von den beiden Personen ist im Verhältnis größer als ihre Mitbürger*innen?
Wir ermitteln die Standardwerte dieser Personen in der entsprechenden Verteilung
Hierbei ist es wichtig, mit den gleichen Maßeinheiten zu arbeiten, da die Körpergröße hier in cm angegeben ist
Der Standardwert der ersten Person ist:
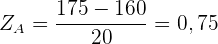
Der Standardwert der zweiten Person ist:
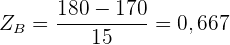
Wenn wir die Werte vergleichen, sehen wir, dass Person größer im Vergleich zu ihren Mitbürger*innen ist, als Person .
Ein Lehrer hat zwei Tests mit einer Gruppe von 
Schülern durchgeführt und kam zu folgenden Ergebnissen: Für den ersten Test ist der Mittelwert und die Standardabweichung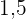 
.
Für den zweiten Test ist der Mittelwert und die Standardabweichung 
.
Ein Schüler bekommt eine im ersten Test und im zweiten eine . In welchem der beiden Tests erhielt er in Bezug auf seine Gruppe eine bessere Punktzahl?
Wir ermitteln die Standardwerte des Schülers in den Verteilungen jedes Tests
Der Standardwert im ersten Test lautet:
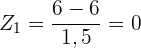
Der Standardwert im zweiten Test lautet:
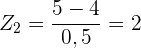
Wenn wir die Werte vergleichen, stellen wir fest, dass er im zweiten Test eine höhere Punktzahl erzielen konnte.
In Sälen eines Kinos waren an einem bestimmten Tag 
und 
Personen anwesend.
-
- Berechne das Streuungsmaß der Anzahl der anwesenden Personen.
-
- Berechne den Variationskoeffizienten.
- Wenn am Tag der Vorstellung Personen mehr in jedem Kinosaal anwesend wären, wie würde sich das auf das Streuungsmaß auswirken?
1 Standardabweichung
Wir bestimmen das arithmetische Mittel
Schließlich berechnen wir die Standardabweichung
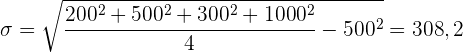
2 Variationskoeffizient
Um den Variationskoeffizienten zu berechnen, müssen wir die Standardabweichung durch das arithmetische Mittel dividieren
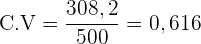
3 Streuungsmaß mit 50 zusätzlichen Personen
Wenn in allen Kinosälen Personen mehr anwesend sind, steigt das arithmetische Mittel auch um Personen. Somit
Die Standardabweichung variiert nicht, da wir den Datensatz um die gleiche Menge erweitern.
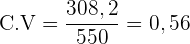
Das relative Streuungsmaß ist geringer als im zweiten Fall.
Du bist auf der Suche nach Nachhilfe in Mathe? Setz dich mit uns Verbindung und wir helfen dir gerne weiter.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
