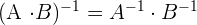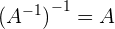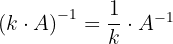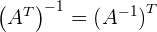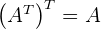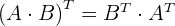Konzept einer Matrix
Als Matrix bezeichnet man eine rechteckige Anordnung von Zahlen oder Ausdrücken, bestehend aus Zeilen und Spalten. Beispiel einer Matrix " "
"
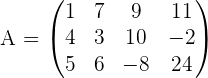
Jede Zahl, die in der Matrix vorkommt, ist ein Element. Somit sind die Elemente unserer vorhergehenden Beispielmatrix die Zahlen 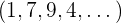 .
.
Die Anzahl der Zeilen und Spalten einer Matrix nennt man die Dimension einer Matrix.
Eine Matrix  mit
mit  Zeilen und
Zeilen und  Spalten können wir
Spalten können wir  benennen (die linke Zahl des Fußindexes gibt immer die Zeilen an, während die rechte Zahl die Spalten angibt) oder
benennen (die linke Zahl des Fußindexes gibt immer die Zeilen an, während die rechte Zahl die Spalten angibt) oder 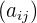 (in Klammern). Ein beliebiges Element, das sich in der Zeile
(in Klammern). Ein beliebiges Element, das sich in der Zeile  und in der Spalte
und in der Spalte 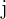 befindet, nennen wir
befindet, nennen wir 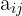 (ohne Klammern). Ein Element unterscheidet sich von einem anderen durch die Position, die es einnimmt. Also die Zeile und die Spalte, zu der es gehört.
(ohne Klammern). Ein Element unterscheidet sich von einem anderen durch die Position, die es einnimmt. Also die Zeile und die Spalte, zu der es gehört.

Beispiel:
Aus dem vorhergehenden Beispiel wissen wir, dass die Elemente unserer Matrix 
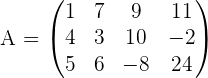
wie folgt sind (je nach deren Position): 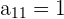 ,
,  ,
,  ,
, 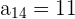 ,
,  ,
, 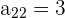 ,
, 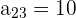 ,
, 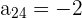 ,
, 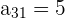 ,
,  ,
,  und
und 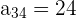 . Außerdem ist ihre Dimension
. Außerdem ist ihre Dimension  Zeilen und
Zeilen und  Spalten, weshalb wir
Spalten, weshalb wir  als
als 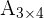 oder
oder  benennen können.
benennen können.
Zwei Matrizen sind gleich, wenn sie dieselbe Dimension haben und die Elemente sich jeweils an der gleichen Stelle befinden und ebenso dieselben sind. Wenn wir also in mathematischer Form die Matrizen 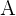 und
und 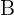 haben:
haben:

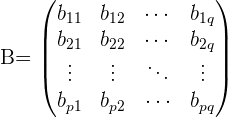
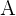 und
und 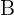 sind gleich, wenn
sind gleich, wenn 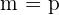 ,
, 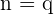 und
und  für irgendeinen Wert
für irgendeinen Wert  und
und 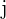 .
.
Beispiel:
Gegeben sind die Matrizen
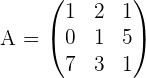
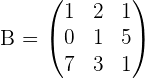
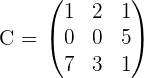
Wir wissen, dass 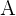 und
und 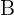 gleich sind, da sie die selbe Dimension haben und die Elemente an den jeweiligen Positionen übereinstimmen. Jedoch sind
gleich sind, da sie die selbe Dimension haben und die Elemente an den jeweiligen Positionen übereinstimmen. Jedoch sind 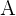 und
und 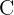 nicht gleich, da
nicht gleich, da 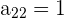 , aber
, aber 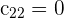 . Deshalb gilt
. Deshalb gilt 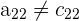 .
.
Rechnen mit Matrizen
Summe aus Matrizen
Gegeben sind die Matrizen 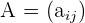 und
und 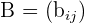 mit derselben Dimension. Ihre Summenmatrix ist:
mit derselben Dimension. Ihre Summenmatrix ist:  . Das heißt, jene Matrix, deren Elemente man erhält, indem man die Elemente der beiden Matrizen, die sich jeweils an der selben Position befinden, addiert (Element plus Element).
. Das heißt, jene Matrix, deren Elemente man erhält, indem man die Elemente der beiden Matrizen, die sich jeweils an der selben Position befinden, addiert (Element plus Element).
Beispiel:
Gegeben sind die Matrizen
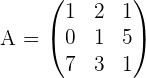

Summe der Matrizen:
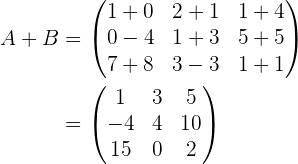
Gesetze
-
- Assoziativ: Gegeben sind die Matrizen
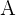 ,
, 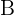 und
und 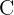 , es gilt
, es gilt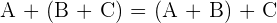 .
.
- Assoziativ: Gegeben sind die Matrizen
-
- Neutrales Element: Es existiert eine Matrix
 . Wenn wir diese Matrix mit der Matrix
. Wenn wir diese Matrix mit der Matrix  addieren, erhalten wir
addieren, erhalten wir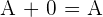 .
.Alle Elemente der Matrix
 sind nur Nullen.
sind nur Nullen.
- Neutrales Element: Es existiert eine Matrix
-
- Additiv Inverses: Für jede Matrix
 existiert eine Matrix
existiert eine Matrix 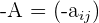 , genannt additiv Inverses für
, genannt additiv Inverses für  :
: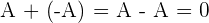 .
.Die Elemente der Matrix
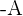 sind die Elemente von A multipliziert mit
sind die Elemente von A multipliziert mit  .
.
- Additiv Inverses: Für jede Matrix
- Kommutativ: Gegeben sind die Matrizen
 und
und 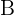 , es gilt
, es gilt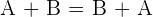 .
.
Produkt aus einer reellen Zahl und einer Matrix
Gegeben ist eine Matrix 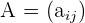 und eine reelle Zahl
und eine reelle Zahl 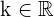 . Das Produkt aus der Matrix und der Zahl ist wie folgt: Jedes Element der Matrix
. Das Produkt aus der Matrix und der Zahl ist wie folgt: Jedes Element der Matrix 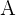 wird der Reihe nach mit
wird der Reihe nach mit  multipliziert, in anderen Worten
multipliziert, in anderen Worten  .
.
Beispiel:
Gegeben ist die Matrix
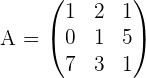
und der reelle Skalar  . Multiplikation der Matrizen
. Multiplikation der Matrizen
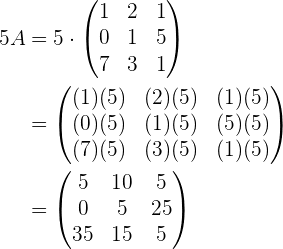
Gesetze
-
- Assoziativität: Gegeben ist die Matrix
 und die Skalare
und die Skalare  y
y  , es gilt
, es gilt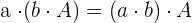 .
.
- Assoziativität: Gegeben ist die Matrix
-
- Distributivität bei den Skalaren : Gegeben ist die Matrix
 und die Skalare
und die Skalare  und
und  , es gilt
, es gilt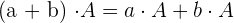 .
.
- Distributivität bei den Skalaren : Gegeben ist die Matrix
-
- Distributivität bei den Matrizen: Gegeben sind die Matrizen
 und
und 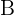 und der Skalar
und der Skalar  , es gilt
, es gilt .
.
- Distributivität bei den Matrizen: Gegeben sind die Matrizen
- Neutraler Skalar: Gegeben ist die Matrix
 und der Skalar
und der Skalar  , es gilt
, es gilt .
.
Produkt aus Matrizen
Zwei Matrizen  und
und 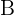 lassen sich nur dann miteinander multiplizieren, wenn die Anzahl der Spalten von
lassen sich nur dann miteinander multiplizieren, wenn die Anzahl der Spalten von  mit der Anzahl der Zeilen von
mit der Anzahl der Zeilen von 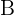 übereinstimmt.
übereinstimmt.
Die Multiplikation zweier multiplizierbarer Matrizen 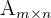 und
und 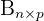 ergibt eine neue Matrix
ergibt eine neue Matrix 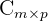 , deren Anzahl der Zeilen mit der Anzahl der Zeilen von
, deren Anzahl der Zeilen mit der Anzahl der Zeilen von  und deren Anzahl der Spalten mit der Anzahl der Spalten von
und deren Anzahl der Spalten mit der Anzahl der Spalten von 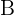 übereinstimmt.
übereinstimmt.

Das Element  der Produktmatrix erhält man, indem man jedes Element der Zeile
der Produktmatrix erhält man, indem man jedes Element der Zeile 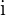 der Matrix
der Matrix 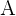 mit jedem Element der Spalte
mit jedem Element der Spalte 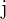 der Matrix
der Matrix 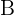 multipliziert und sie addiert
multipliziert und sie addiert 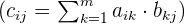 .
.
Beispiel:
Gegeben sind die Matrizen
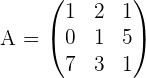

Multiplikation der Matrizen:
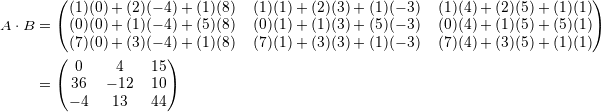
Gesetze
-
- Assoziativ: Gegeben sind die Matrizen
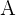 ,
, 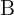 und
und 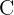 , es gilt
, es gilt .
.
- Assoziativ: Gegeben sind die Matrizen
-
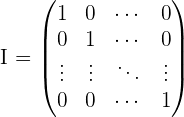
- Neutrales Element: Gegeben ist die Matrix
 , für die eine Matrix
, für die eine Matrix 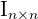 existiert. Es gilt
existiert. Es gilt .
.Die Diagonale der Matrix
 enthält ausschließlich
enthält ausschließlich  , alle anderen Zahlen sind
, alle anderen Zahlen sind 
- Neutrales Element: Gegeben ist die Matrix
-
- Nicht-kommutativ: Gegeben sind die Matrizen
 und
und 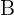 . Für die meisten Fälle gilt
. Für die meisten Fälle gilt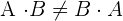 .
.
- Nicht-kommutativ: Gegeben sind die Matrizen
- Distributivität des Produkts in Bezug auf die Summe: Für die gegebenen Matrizen
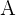 ,
, 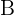 und
und 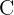 gilt
gilt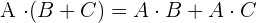 .
.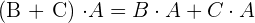 .
.
Inverse Matrix
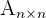 ist eine Matrix mit der gleichen Anzahl an Zeilen und Spalten. Wenn eine Matrix
ist eine Matrix mit der gleichen Anzahl an Zeilen und Spalten. Wenn eine Matrix 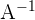 existiert, für die gilt
existiert, für die gilt
 ,
,
wobei 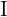 die Einheitsmatrix ist, sagen wir, die Matrix
die Einheitsmatrix ist, sagen wir, die Matrix 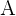 ist invertierbar oder regulär. Außerdem ist
ist invertierbar oder regulär. Außerdem ist  die inverse Matrix zu
die inverse Matrix zu 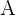 .
.
Beispiel:
Gegeben ist die Matrix
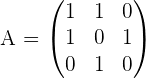
.
Inverse Matrix:
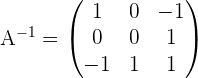
Um dies zu überprüfen, sehen wir uns Folgendes an
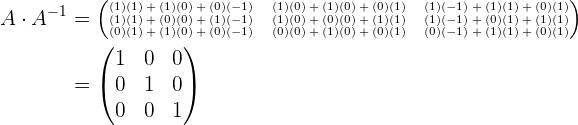
Gesetze
Arten von Matrizen
1. Zeilenmatrix
Eine Matrix, die nur aus einer Zeile besteht.

Beispiel:

2. Spaltenmatrix
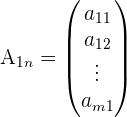
Beispiel:
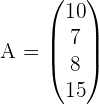
3. Rechteckige Matrix
Bei dieser Matrix stimmt die Anzahl der Zeilen nicht mit der Anzahl der Spalten überein, ihre Dimension ist  .
.

Beispiel:
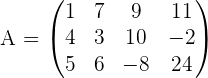
4. Quadratische Matrix
Die Anzahl der Zeilen stimmt mit der Anzahl der Spalten überein.
Die Elemente der Form 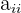 bilden die Hauptdiagonale.
bilden die Hauptdiagonale.
Die Nebendiagonale besteht aus den Elementen, für deren Indizes Folgendes gilt: 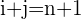
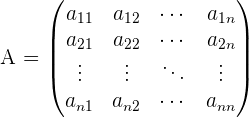
Beispiel:
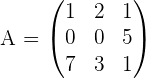
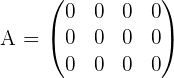
5 Nullmatrix
Alle Elemente sind null.

Wobei 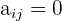 für alle
für alle  und
und 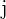 .
.
Beispiel:
6. Obere Dreiecksmatrix
Die Elemente unterhalb der Hauptdiagonalen sind  .
.

Beispiel:

Da die Definition von der Hauptdiagonalen abhängt, muss die Matrix quadratisch sein.
7. Untere Dreiecksmatrix
Die Elemente oberhalb der Hauptdiagonalen sind  .
.
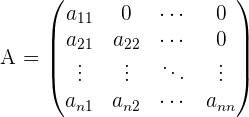
Beispiel:
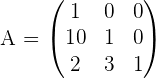
Da die Definition von der Hauptdiagonalen abhängt, muss die Matrix quadratisch sein.
8. Diagonalmatrix
Alle Elemente außerhalb der Hauptdiagonalen sind null.

Beispiel:
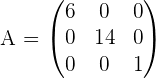
Da es sich um Dreiecksmatrizen handelt, sind die Matrizen quadratisch.
9. Skalarmatrix
Eine Diagonalmatrix, bei der alle Elemente der Hauptdiagonalen gleich sind.
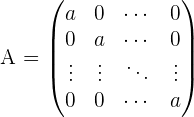
Beispiel:

Da es sich um eine Diagonalmatrix handelt, ist die Matrix quadratisch.
10. Einheitsmatrix
Eine Diagonalmatrix, bei der die Elemente der Hauptdiagonalen 1 sind.
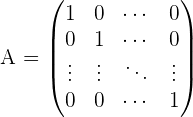
Beispiel:
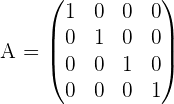
Da es sich um eine Skalarmatrix handelt, ist die Matrix quadratisch.
11. Transponierte Matrix
Die transponierte Matrix einer Matrix A ist die Matrix, die man erhält, wenn man die Zeilen und Spalten vertauscht (die erste Zeile wird zur ersten Spalte usw.). Wenn wir die Matrix 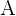 haben,
haben,

ist deren transponierte Matrix  , für die gilt
, für die gilt

Beispiel:
Gegeben ist die Matrix

deren transponierte Matrix
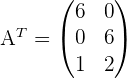
ist.
Eigenschaften:
12. Reguläre Matrix
Quadratische Matrix, die eine Inverse besitzt.
13. Singuläre Matrix
Matrix, deren inverse Matrix nicht existiert. Zum Beispiel existiert für keine rechteckige Matrix (nicht quadratisch) eine Inverse (eine Matrix muss quadratisch sein, damit eine Inverse existiert).
14. Idempotente Matrix
Für eine idempotente Matrix gilt:
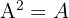
Beispiel:
Sehen wir uns folgende Matrix an
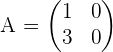
,
Wir stellen fest, dass
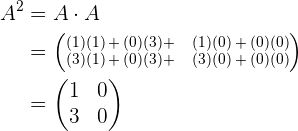
15. Selbstinverse Matrix
Für eine selbstinverse Matrix gilt:
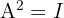
Beispiel:
Wir sehen uns folgende Matrix an
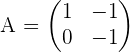
,
Wir stellen fest, dass
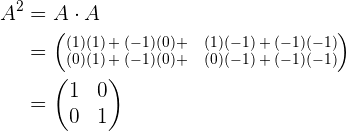
16. Symmetrische Matrix
Für eine symmetrische Matrix gilt
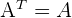
Beispiel:
Wir sehen uns folgende Matrix an

,
Wir stellen fest, dass
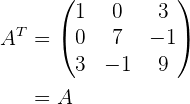
.
17. Antisymmetrische oder schiefsymmetrische Matrix
Für eine antisymmetrische Matrix gilt:
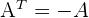
Beispiel:
Wir sehen uns folgende Matrix an
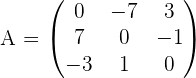
,
Wir stellen fest, dass
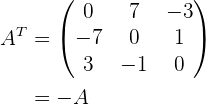
.
18. Orthogonale Matrix
Für eine orthogonale Matrix gilt:
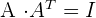
Beispiel:
Wir sehen uns folgende Matrix an

,
Wir stellen fest, dass ihre transponierte Matrix
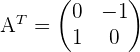
,
ist.
Wir multiplizieren 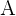 mit ihrer transponierten Matrix
mit ihrer transponierten Matrix  und erhalten
und erhalten
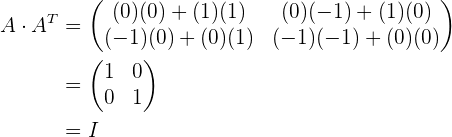
.
Denk daran, dass du bei Superprof auch Einzelnachhilfe in Mathe mit einem*r privaten Nachhilfelehrer*in finden kannst, falls du bei den Matrizen noch etwas Unterstützung brauchst.
Mit KI zusammenfassen: