Eine Exponentialgleichung ist eine Gleichung, bei der die Variable im Exponenten auftaucht.
Um eine Exponentialgleichung zu lösen, müssen wir Folgendes beachten:
Potenzgesetze
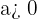
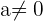
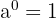
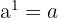
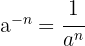
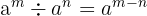
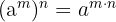
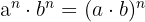
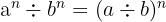
- wenn
, ist 
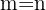
Exponentialgleichungen lösen
Fall 1: Exponentialgleichungen mit gleicher Basis
Die nötigen Schritte zur Bildung einer gleichen Basis durchführen, sodass wir die Exponenten gleichsetzen können.
Beispiele
1 
Wir formen die rechte Seite in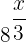 
um und zerlegen die Zahl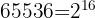 
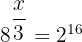
Da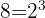 
, gilt:
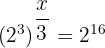
Wir setzen die Potenzen gleich
2 
Wir wandeln die Wurzeln in Potenzen mit einem Bruch als Exponent um und setzen die Exponenten gleich
Wir lösen die sich daraus ergebende Gleichung:
3 
Wir klammern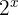 
aus
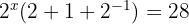
Wir wenden die Regel zum Umgang mit negativen Potenzen an und führen die erforderlichen Schritte durch. Wir erhalten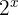
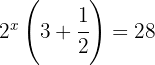
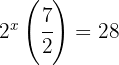
Wir formen die Gleichung um, sodass beide Seiten die gleiche Basis haben und setzen die Exponenten gleich
Fall 2: Die Summe der Terme bei einer geometrischen Folge
Wenn wir die Summe von 
Termen einer geometrischen Folge haben, wenden wir folgende Formel an:
Beispiel
Anwenden der Formel:
Wir bestimmen 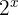und formen so um, dass beide Seiten die gleiche Basis haben
Fall 3: Substitution
Wenn wir eine komplexere Gleichung haben, können wir zur Lösung auf die Substitution zurückgreifen.
Beispiele
1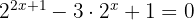 
Zuerst wenden wir die Regel zum Produkt von Potenzen an, um die Gleichung zu vereinfachen.
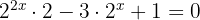
Wir wenden die Regel zur Potenzierung von Potenzen an
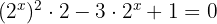
Wir substituieren 
Wir faktorisieren die Gleichung und erhalten
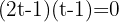
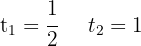
Wir führen die Rücksubstitution durch
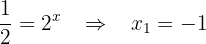
2 
Wir wenden die Regeln zu Potenzen von Produkt oder Quotient an, um die Summe oder Differenz aus den Exponenten zu entfernen
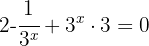
Wir substituieren 
Wir multiplizieren beide Terme mit 
Wir faktorisieren und lösen die Gleichung
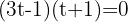
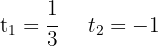
Wir führen die Rücksubstitution durch
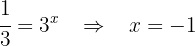
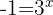
Bei der zweiten Gleichung erhalten wir keine Lösung
3 
Wir zerlegen in die Faktoren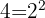 
und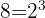
Wir substituieren
Wir führen die Rücksubstitution nur mit der positiven Lösung durch.
Da wir keine Exponenten gleichsetzen können, logarithmieren wir beide Seiten der Gleichung und wenden auf der linken Seite der Gleichung die Regel an:
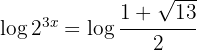
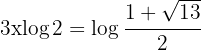
Wir bestimmen 
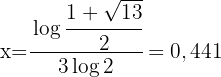
Für die negative Lösung erhalten wir keine Lösungsmenge, da wir beim Anwenden des Logarithmus im zweiten Term den Logarithmus einer negativen Zahl erhalten. Dieser existiert nicht.
Fall 4: Ungleiche Basis
Um eine Variable, die sich im Exponent einer Potenz befindet, zu bestimmen, wendet man den Logarithmus, dessen Basis die Basis der Potenz ist, an.
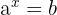
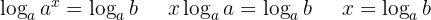
Beispiel
1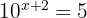 
Auf beiden Seiten der Gleichung logarithmieren
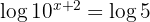
Wir wenden die Regel zum Logarithmus einer Potenz an
Es gilt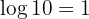 
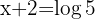
Wir bestimmen
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut