Definition des Logarithmus
Der Exponent, mit dem eine Zahl, die Basis, potenziert werden muss, um eine festgelegte Zahl zu erhalten. Ein Logarithmus ermittelt den Exponenten 
einer Basis 
, der verwendet wurde, um ein bestimmtes Ergebnis 
zu erhalten.
Beispiel:
Wenn die Basis 
und das Ergebnis 
ist, welchen Exponenten muss die Zahl 
haben, damit das Ergebnis 
ist? Wie du siehst, ist der Wert des Exponenten, der genutzt wurde, um das Ergebnis mit der Basis zu erhalten, 
.
Ein Logarithmus wird wie folgt notiert:
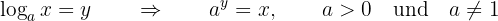
ist hierbei die Basis, das Ergebnis und der gesuchte Exponent. Die Basis muss positiv und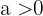 
ungleich 1 sein .
Anhand der Definition des Logarithmus ergibt sich:
- Es gibt keinen Logarithmus zu einer negativen Basis.
- Es gibt keinen Logarithmus einer negativen Zahl.
- Es gibt keinen Logarithmus von Null.
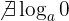
- Der Logarithmus von 1 ist 0.
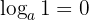
- Der Logarithmus von
a zur Basis a ist gleich 
.
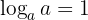
- Der Logarithmus zur Basis a einer Potenz zur Basis a ist gleich dem Exponenten.
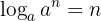
Eigenschaften von Logarithmen
1 Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der Faktoren:
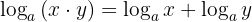
Beispiel:
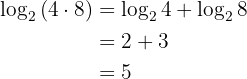
2 Der Logarithmus eines Quotienten ist gleich dem Logarithmus des Dividenden minus dem Logarithmus des Divisors:
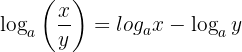
Beispiel:
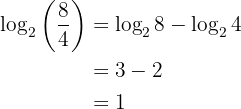
3 Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Exponenten und dem Logarithmus der Basis:
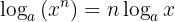
Beispiel:
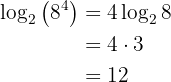
4 Der Logarithmus einer Wurzel ist gleich dem Quotienten aus dem Logarithmus des Radikanden und dem Wurzelexponenten der Wurzel:
Beispiel:
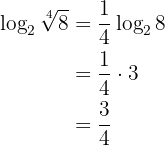
5 Wechsel der Basis:
Beispiel:
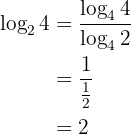
Seit ihrer Entstehung sind Logarithmen zu einem wichtigen Werkzeug für das Rechnen mit sehr großen Zahlen geworden, da sie die Eigenschaft haben, mit Exponenten zu arbeiten und aus der Multiplikation eine Addition zu machen. Der Logarithmus ermöglicht dank seiner Eigenschaften auch die Vereinfachung verschiedener mathematischer Operationen. Es lohnt sich also, sich näher mit dem Logarithmus zu befassen.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut