Löse folgende Exponentialgleichungen
1 
2 
3 
4 
5 
6 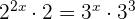
7 
8 
9 
10 
11 
12 
Lösen von Exponentialgleichungen:
1
Wir schreiben 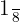 als Potenz und setzen die Exponenten gleich
als Potenz und setzen die Exponenten gleich




2
Die Wurzel schreiben wir als Potenz mit einem Bruch als Exponent und  zerlegen wir in Faktoren
zerlegen wir in Faktoren

Wir setzen die Exponenten gleich
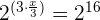

3
Wir zerlegen  und
und  in Faktoren, setzen die Exponenten gleich und vereinfachen die Gleichung
in Faktoren, setzen die Exponenten gleich und vereinfachen die Gleichung
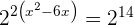


Wir lösen die Gleichung
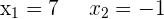
4
Wir zerlegen  in Faktoren, setzen die Exponenten gleich und lösen die irrationale Gleichung
in Faktoren, setzen die Exponenten gleich und lösen die irrationale Gleichung



5
Da wir unterschiedliche Basen haben, logarithmieren wir beide Seiten der Gleichung
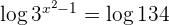
Wir wenden die Regel für den Logarithmus einer Potenz auf der linken Seite der Gleichung an
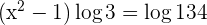
Wir bringen  auf die andere Seite und lösen die Gleichung
auf die andere Seite und lösen die Gleichung
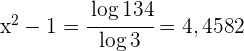


6
Wir bringen  und
und  auf die jeweils andere Seite der Gleichung
auf die jeweils andere Seite der Gleichung
Wir logarithmieren mit der Basis 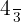 beide Seiten der Gleichung
beide Seiten der Gleichung

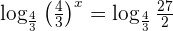
Auf der linken Seite wenden wir die Regel für den Logarithmus einer Potenz an
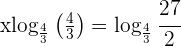
Dabei beachten wir:
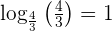
Wir führen die Substitution durch

7
Wir logarithmieren beide Seiten der Gleichung und wenden die Regel für den Logarithmus eines Produkts auf der linken Seite der Gleichung an
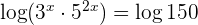

Wir wenden die Regel für den Logarithmus einer Potenz an und klammern  aus
aus
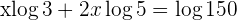

Wir wenden die Regel für den Logarithmus einer Potenz und eines Produktes an
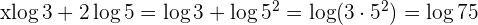
Wir bestimmen die Variable

8
Wir wenden die Regel für die Potenz des Quotienten an, um die Differenz aus dem Exponenten zu entfernen. Danach führen wir die Substitution durch


Wir lösen die Gleichung

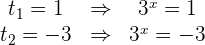

 hat keine Lösung, da eine Potenz mit positiver Basis keine negative Zahl sein kann
hat keine Lösung, da eine Potenz mit positiver Basis keine negative Zahl sein kann
9
Wir führen die Substitution durch

Wir lösen die Gleichung und führen die Rücksubstitution durch

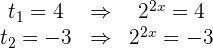

 hat keine Lösung, da eine Potenz mit positiver Basis keine negative Zahl sein kann
hat keine Lösung, da eine Potenz mit positiver Basis keine negative Zahl sein kann
10
Wir wandeln die negativen Exponenten um, lösen den Bruch auf und substituieren
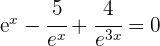
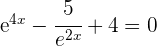

Wir lösen die Gleichung und führen die Rücksubstitution durch
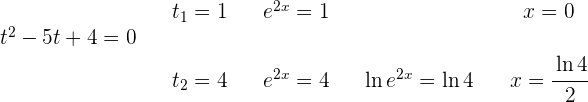
11
Wir wenden die Formel zur Berechnung der Partialsumme von  einer geometrischen Folge an bringen beide Seiten auf den gleichen Nenner
einer geometrischen Folge an bringen beide Seiten auf den gleichen Nenner
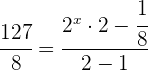
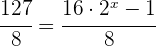
Wir kürzen und erhalten



12
Wir zerlegen  in Faktoren und wenden die Regel für das Produkt und den Quotienten von Potenzen an, um die Summe und Differenz aus den Exponenten zu entfernen. Danach führen wir die Substitution durch.
in Faktoren und wenden die Regel für das Produkt und den Quotienten von Potenzen an, um die Summe und Differenz aus den Exponenten zu entfernen. Danach führen wir die Substitution durch.



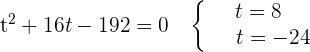
Wir führen die Rücksubstitution durch

 hat keine Lösung, da eine Potenz mit positiver Basis nicht negativ sein kann
hat keine Lösung, da eine Potenz mit positiver Basis nicht negativ sein kann
Löse folgende Exponentialgleichungssysteme
1 
2 
3 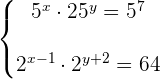
Exponentialgleichungssysteme lösen:
1
Wir multiplizieren beide Seiten der Gleichung mit dem Nenner des Bruchs. Auf der rechten Seite der Gleichung wenden wir die Regel für das Produkt von Potenzen mit gleicher Basis an
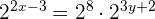
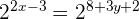
Wir setzen die Exponenten gleich
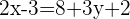

Wir lösen das Gleichungssystem
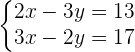

2
Wir wenden die Regel für den Quotient von Potenzen an, um die Differenzen aus den Exponenten zu entfernen. Danach führen wir die Substitution durch

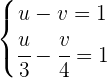
Wir beseitigen die Brüche in der ersten Gleichung und lösen das Gleichungssystem


Wir führen die Rücksubstitution durch
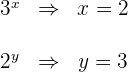
3
Bei der ersten Gleichung  und bei der zweiten Gleichung wenden wir die Regel für das Produkt und den Quotienten von Potenzen an, um die Summen und Differenzen aus den Exponenten zu entfernen
und bei der zweiten Gleichung wenden wir die Regel für das Produkt und den Quotienten von Potenzen an, um die Summen und Differenzen aus den Exponenten zu entfernen
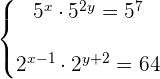
Wir multiplizieren die Potenzen mit gleicher Basis bei beiden Gleichungen

Wir setzen die Exponenten gleich und lösen das Gleichungssystem
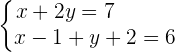

Löse folgende Logarithmusgleichungen
1 
2 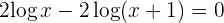
3 
4 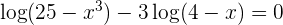
5 
6 
Lösen von Logarithmusgleichungen:
1
Wir wenden die Regel für den Logarithmus einer Potenz und die Regel für den Logarithmus eines Produkts an

Numerivergleich

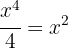
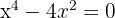
Wir lösen die Gleichung:

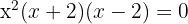
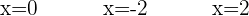
Weder  noch
noch  stellen eine Lösung dar. Wenn wir sie in die Gleichung einsetzen, finden wir den Logarithmus von
stellen eine Lösung dar. Wenn wir sie in die Gleichung einsetzen, finden wir den Logarithmus von  und den Logarithmus einer negativen Zahl vor und diese Art von Logarithmen existieren nicht
und den Logarithmus einer negativen Zahl vor und diese Art von Logarithmen existieren nicht
Die einzige Lösung ist 
2
Wir wenden die Regel für den Logarithmus einer Potenz an und auf der rechten Seite der Gleichung schreiben wir 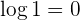

Wir wenden die Regel für den Logarithmus eines Quotienten an und machen den Numerivergleich
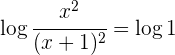
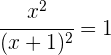
Wir lösen den Bruch auf und lösen die Gleichung
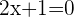

Allerdings stellt  keine Lösung dar. Wenn wir es in die Gleichung einsetzen, erhalten wir den Logarithmus einer negativen Zahl
keine Lösung dar. Wenn wir es in die Gleichung einsetzen, erhalten wir den Logarithmus einer negativen Zahl
3
Wir lösen den Bruch auf und führen die Substitution durch
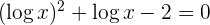
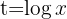
Wir lösen die Gleichung
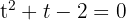

Wir führen die Rücksubstitution durch die Definition des Logarithmus durch

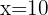
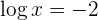
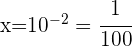
4
Wir bringen den zweiten Summanden auf die rechte Seite der Gleichung und wenden die Regel für den Logarithmus einer Potenz an. Danach erfolgt der Numerivergleich
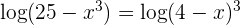

Wir führen die nötigen Rechenschritte durch
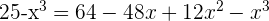
Wir lösen die Gleichung

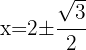
5
Wir lösen den Bruch auf
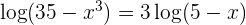
Auf der rechten Seite der Gleichung wenden wir die Regel für den Logarithmus einer Potenz an und führen den Numerivergleich durch

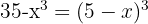
Wir führen die nötigen Rechenschritte durch und lösen die Gleichung zweiten Grades


6
Wir multiplizieren beide Seiten der Gleichung mit 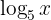 und bringen alles auf die linke Seite der Gleichung
und bringen alles auf die linke Seite der Gleichung
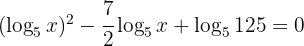

Wir lösen den Bruch auf und führen die Substitution durch
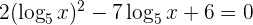
Wir lösen die Gleichung
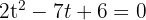


Löse folgende logarithmische Gleichungssysteme
1 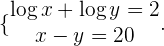
2 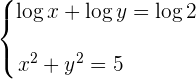
3 
4 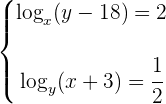
Lösen von logarithmischen Gleichungssystemen:
1
Bei der ersten Gleichung wenden wir die Regel für den Logarithmus eines Produkts an und führen den Numerivergleich durch. Wir erhalten 
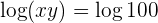
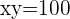
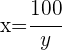
Wir setzen den Wert für  in die zweite Gleichung ein
in die zweite Gleichung ein
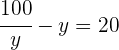
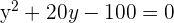
Wir lösen die Gleichung zweiten Grades

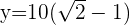
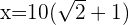
2
Bei der ersten Gleichung wenden wir die Regel für den Logarithmus eines Produkts an. Danach führen wir den Numerivergleich durch und erhalten 
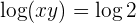
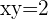
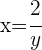
Wir setzen den Wert für  in die zweite Gleichung ein
in die zweite Gleichung ein
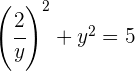

Wir lösen die Gleichung zweiten Grades
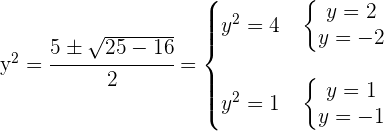

Wenn wir für  negative Werte in die Gleichung einsetzen, erhalten wir den Logarithmus einer negativen Zahl. Dasselbe gilt für
negative Werte in die Gleichung einsetzen, erhalten wir den Logarithmus einer negativen Zahl. Dasselbe gilt für 
3
Wir multiplizieren die erste Gleichung mit 

Wir wenden die Definition des Logarithmus an, um  zu bestimmen
zu bestimmen

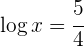
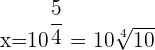
Wir setzen den Wert für  in die erste Anfangsgleichung ein
in die erste Anfangsgleichung ein
Wir wenden die Definition des Logarithmus an, um  zu bestimmen
zu bestimmen


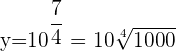
4
Wir wenden bei beiden Gleichungen die Definition des Logarithmus an
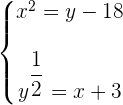
Wir wandeln die zweite Gleichung in eine quadratische Gleichung um und setzen den Wert für y in die erste Gleichung ein
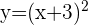
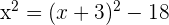
Wir führen die nötigen Rechenschritte durch und lösen die Gleichung
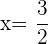
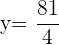
Mit KI zusammenfassen:



Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut