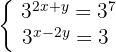
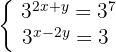
1
Da die Basen der Potenzen in beiden Teilen der Gleichung dieselben sind, werden die Exponenten angeglichen und das  -Gleichungssystem wird aufgelöst. Erinnere dich daran, dass bei Potenzen mit Exponent
-Gleichungssystem wird aufgelöst. Erinnere dich daran, dass bei Potenzen mit Exponent  dieser normalerweise nicht sichtbar ist.
dieser normalerweise nicht sichtbar ist.
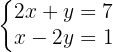
2
Multipliziere die erste Gleichung mit 

Addiere nun beide Gleichungen Term für Term
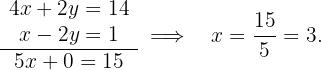
Den Wert für  erhältst du, indem du den Wert für
erhältst du, indem du den Wert für  auf einer der beiden Seiten einsetzt:
auf einer der beiden Seiten einsetzt:
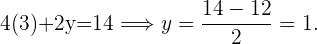
Die Lösung der Gleichung ist folglich 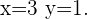
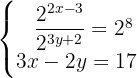
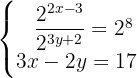
1
Um eine Potenz derselben Basis in der gesamten Gleichung zu erhalten, löse zunächst den Bruch der ersten Gleichung auf:

Die Exponenten der ersten Gleichung können jetzt miteinander gleichgesetzt werden, da ihre Potenzen dieselbe Basis haben. Vereinfache nun die Gleichung:

Ziehe für das  -Gleichungssystem die ursprüngliche zweite Gleichung heran und löse auf
-Gleichungssystem die ursprüngliche zweite Gleichung heran und löse auf
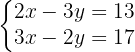
2
indem du die erste Gleichung mit  und die zweite mit
und die zweite mit  multiplizierst
multiplizierst
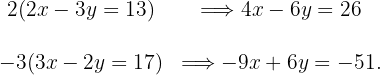
Addiere nun beide Gleichungen Term für Term und du erhältst den Wert für  :
:
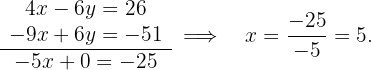
Den Wert für  erhältst du, indem du den Wert für
erhältst du, indem du den Wert für  auf einer der beiden Seiten einsetzt:
auf einer der beiden Seiten einsetzt:

Die Lösung der Gleichung ist folglich 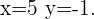
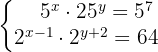
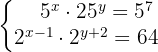
1
Mache dir die Eigenschaften des Potenzprodukts zunutze, um beide Gleichungen zu vereinfachen und auf jeweils einen Exponenten zu bringen
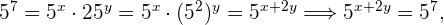
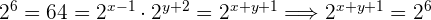
Bilde das  -Gleichungssystem indem du die Exponenten aus beiden Gleichungen miteinander gleichsetzt, da sie auf beiden Seiten dieselbe Basis haben
-Gleichungssystem indem du die Exponenten aus beiden Gleichungen miteinander gleichsetzt, da sie auf beiden Seiten dieselbe Basis haben
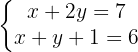
2
Das Substitutionsverfahren besteht darin, eine von zwei Variablen einer Gleichung zu ermitteln und anschließend das Ergebnis bzw. den so erhaltenen Term in die zweite Gleichung einzusetzen, um den Wert der zweiten Variablen herauszufinden:
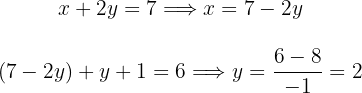
Durch Einsetzen des Werts von  in der Gleichung
in der Gleichung 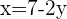 erhält man
erhält man  . Die Lösung der Gleichung ist folglich
. Die Lösung der Gleichung ist folglich 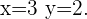
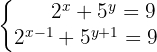
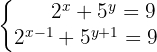
1
Wende bei der zweiten Gleichung das Potenzgesetz an, um die Summen und Subtraktionen in den Exponenten als Produkt und Bruch darzustellen:
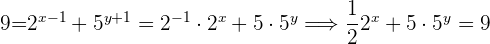
Durch Tausch der Variablen  und Einsetzen in den zuvor erhaltenen Ausdruck und in die erste Gleichung erhält man das
und Einsetzen in den zuvor erhaltenen Ausdruck und in die erste Gleichung erhält man das  -Gleichungssystem
-Gleichungssystem
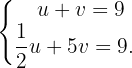
2
Das Substitutionsverfahren besteht darin, eine von zwei Variablen einer Gleichung zu ermitteln und anschließend das Ergebnis bzw. den so erhaltenen Term in die zweite Gleichung einzusetzen, um den Wert der zweiten Variablen herauszufinden. In diesem Fall soll nach der Variablen  aufgelöst werden:
aufgelöst werden:
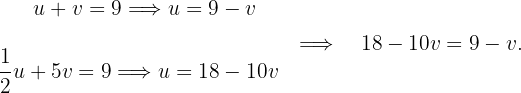
Berechne den Wert von  und setze ihn in einer der Gleichungen des Gleichungssystems ein, um den Wert für
und setze ihn in einer der Gleichungen des Gleichungssystems ein, um den Wert für  zu ermitteln. Setze die erhaltenen Werte für
zu ermitteln. Setze die erhaltenen Werte für  und
und  nun wieder in die Gleichung ein, um die Werte für
nun wieder in die Gleichung ein, um die Werte für  zu erhalten.
zu erhalten.
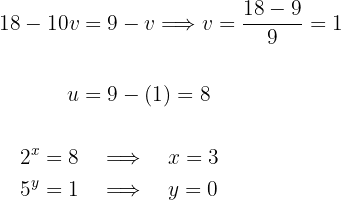
Die Lösung der Gleichung ist folglich 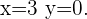
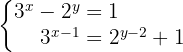
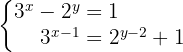
1
Wende bei der zweiten Gleichung das Potenzgesetz and, um die in der Potenz erscheinenden Subtraktionen als Divisionen darzustellen:
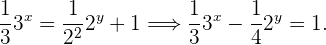
Durch Tauschen der Variablen  und Einsetzen in den zuvor erhaltenen Ausdruck und in die erste Gleichung erhält man das
und Einsetzen in den zuvor erhaltenen Ausdruck und in die erste Gleichung erhält man das  -Gleichungssystem
-Gleichungssystem
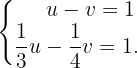
2
Löse in beiden Gleichungen nach  auf und wende das Gleichsetzungsverfahren an, um eine Gleichung mit der Variablen
auf und wende das Gleichsetzungsverfahren an, um eine Gleichung mit der Variablen  zu erhalten
zu erhalten
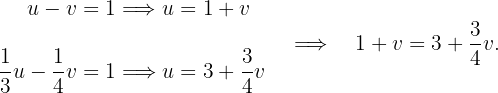
Berechne den Wert von  und setze ihn in eine der Gleichungen des Gleichungssystems ein, um den Wert für
und setze ihn in eine der Gleichungen des Gleichungssystems ein, um den Wert für  zu ermitteln. Setze die erhaltenen Werte für
zu ermitteln. Setze die erhaltenen Werte für  und
und  nun wieder in die Gleichung ein, um die Werte für
nun wieder in die Gleichung ein, um die Werte für  zu erhalten.
zu erhalten.
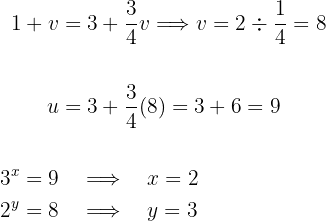
Die Lösung der Gleichung ist folglich 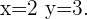
Mit KI zusammenfassen:



Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut