Kapitel
Um die folgenden Aufgaben lösen zu können, hier zur Erinnerung die Rechenregel für Logarithmen, die besagt:
wenn 
der Logarithmus von 
zur Basis 
ist
,
so ist im Umkehrschluss 
.
Das heißt, das Ergebnis des Logarithmierens gibt an, mit welchem Exponenten man die Basis potenzieren muss, um den Numerus zu erhalten.
Berechne anhand dieser Regel die folgenden Aufgaben.
Berechne den Wert von y anhand der Logarithmus-Regel
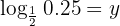
Gegeben sei die Gleichung
Man wendet die Rechenregel für Logarithmen an und wandelt 
in einen Bruch um, das heißt 
, anschließend vereinfacht man die Gleichung
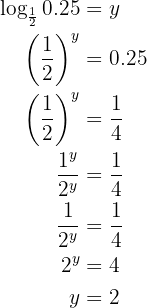
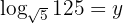
Gegeben sei die Gleichung
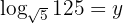
Man wendet die Rechenregel für Logarithmen an und löst auf
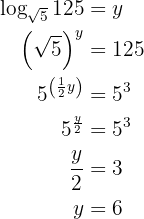
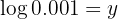
Gegeben sei die Gleichung
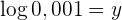
Der Ausdruck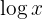 
bedeutet dabei immer, dass 
die Basis ist, das heißt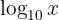 
. Man wendet die Rechenregel für Logarithmen an und löst auf
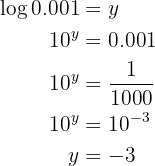
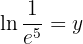
Gegeben sei die Gleichung
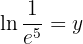
Ein Logarithmus mit Basis 
wird immer als "natürlicher Logarithmus" bezeichnet und als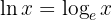 
dargestellt. Man wendet die Rechenregel für Logarithmen an und löst auf
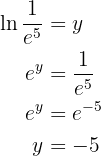
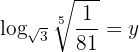
Gegeben sei die Gleichung
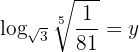
Man wendet die Rechenregel für Logarithmen an und löst auf
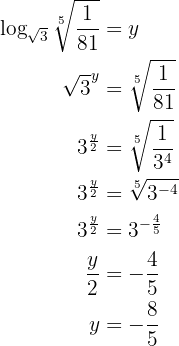
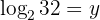
Gegeben sei die Gleichung
3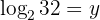
Man wendet die Rechenregel für Logarithmen an und löst auf
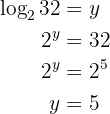
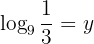
Gegeben sei die Gleichung
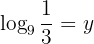
Man wendet die Rechenregel für Logarithmen an und löst auf
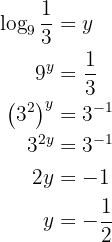
Gegeben sei die Gleichung
Man wendet die Rechenregel für Logarithmen an und löst auf
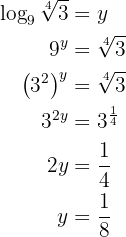
Gegeben sei die Gleichung
Man wendet die Rechenregel für Logarithmen an und löst die Gleichung auf. In diesem Fall verläuft die Auflösung etwas anders, da die Basis des Logarithmus ist.
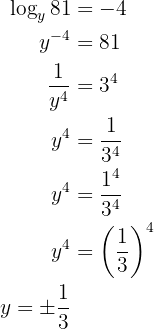
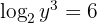
Gegeben sei die Gleichung
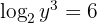
Man wendet die Rechenregel für Logarithmen an und löst die Gleichung auf. In diesem Fall verläuft die Auflösung etwas anders, da Teil des logarithmischen Ausdrucks ist
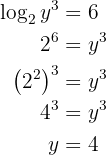
Berechne den Logarithmus
In den Übungen 11 bis 14 wendet man den Basiswechsel der Logarithmen an, der besagt, dass ein Logarithmus von 
mit Basis gleich
mit neuer Basis 
ist. Der Ausdruck rechts enthält bereits die neue Basis.
Gegeben sei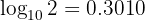 
. Berechne den folgenden Logarithmus:
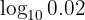
Gegeben sei die Gleichung
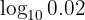
Man wandelt den logarithmischen Ausdruck in einen Bruch um und löst auf
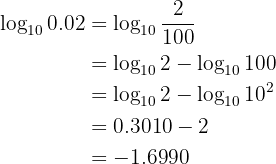
Gegeben sei 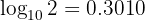. Berechne den folgenden Logarithmus:
Gegeben sei der Logarithmus
Man schreibt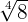 
als Potenz von 
aus.
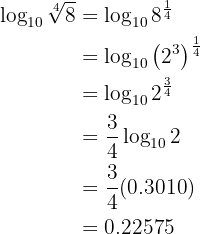
Gegeben sei 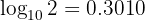. Berechne den folgenden Logarithmus:
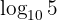
Gegeben sei der Logarithmus
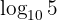
Man schreibt 
zu 
um und wenden dann Logarithmusgesetze an
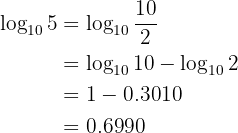
Gegeben sei 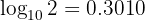. Berechne den folgenden Logarithmus:
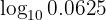
Gegeben sei der Logarithmus
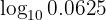
Man schreibt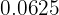 
zu einem Bruch mit Potenz um und wendet dann Logarithmusgesetze an
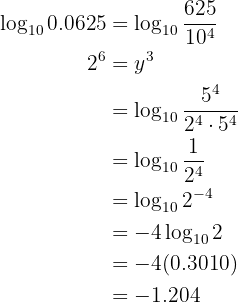
Schreibe den Logarithmus um
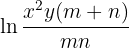
Gegeben sei der Ausdruck
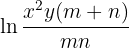
Man löst die Übung wie folgt:
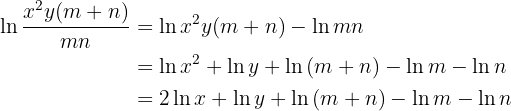
Gegeben sei der Ausdruck
Man löst die Übung wie folgt:
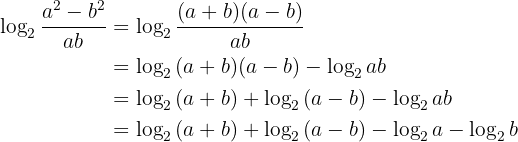
Gegeben sei der Ausdruck
Man löst die Übung wie folgt:
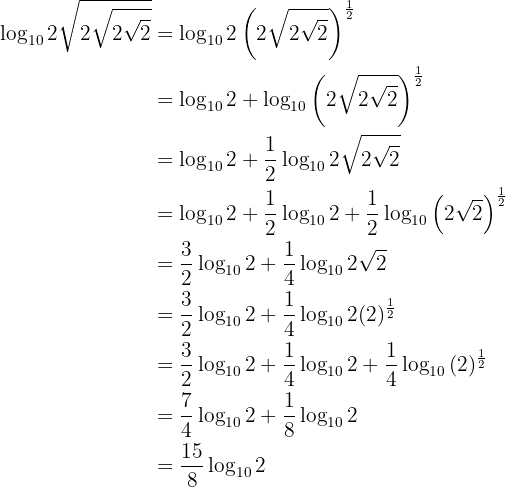
Man erhält den Wert von , indem man Logarithmen anwendet
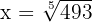
Gegeben sei die Gleichung
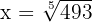
Man löst die Übung wie folgt:
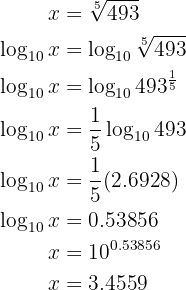
Gegeben sei die Gleichung
Man löst die Übung wie folgt:
Gegeben sei die Gleichung
Man löst die Übung wie folgt:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut