
Definition
Du hast dich sicherlich schon mit Potenzen befasst und weißt zum Beispiel:
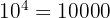
Angenommen, du möchtest aber eine Potenz, bei der die Zahl 10 potenziert wird und das Ergebnis 10000000 ist, herausfinden. Dies kann wie folgt dargestellt werden:
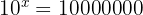
Kannst du bei dieser Gleichung ' ' bestimmen?
' bestimmen?
Die Gleichung, die wir aufstellen, ist eine Exponentialgleichung. Um die Variable ' ' zu bestimmen, müssen wir einen Logarithmus anwenden. Ein Logarithmus ist eine "Rechenoperation" oder "Funktion", mit der man die Potenz erhält, deren gegebene Basis potenziert werden muss, um ein bestimmtes Ergebnis zu erhalten. In unserem Beispiel ist 10 die Basis und das gewünschte Ergebnis ist 10000000. Deshalb gilt:
' zu bestimmen, müssen wir einen Logarithmus anwenden. Ein Logarithmus ist eine "Rechenoperation" oder "Funktion", mit der man die Potenz erhält, deren gegebene Basis potenziert werden muss, um ein bestimmtes Ergebnis zu erhalten. In unserem Beispiel ist 10 die Basis und das gewünschte Ergebnis ist 10000000. Deshalb gilt:
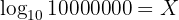
Im Allgemeinen gilt für den Logarithmus:
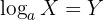
hierbei:
a ist die Basis
x ist das gewünschte Ergebnis (auch Potenzwert genannt)
y ist die Potenz, deren Basis a potenziert wird
Als Nächstes zeigen wir dir anhand von ein paar Beispielen, wie man eine Exponentialgleichung als Logarithmusgleichung darstellt:
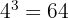

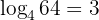
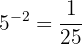

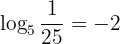


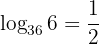
Es ist zu betonen, dass die meist verwendeten Basen bei Logarithmen  und
und  sind (Eulersche Zahl,
sind (Eulersche Zahl, 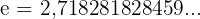 )
)
Wenn die Zahl  die Basis ist, muss sie nicht geschrieben werden:
die Basis ist, muss sie nicht geschrieben werden:
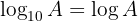
Der Logarithmus zur Basis  heißt natürlicher Logarithmus und wird wie folgt ausgedrückt:
heißt natürlicher Logarithmus und wird wie folgt ausgedrückt:

Regeln für den Logarithmus
1 Der Logarithmus eines Produkts ist die Summe der Logarithmen der einzelnen Faktoren
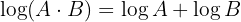
2 Der Logarithmus eines Quotienten ist die Differenz des Logarithmus des Dividenden und des Logarithmus des Divisors
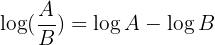
3 Der Logarithmus einer Potenz ist das Produkt aus dem Exponenten und dem Logarithmus der Basis der Potenz
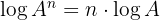
4 Der Logarithmus einer Wurzel ist der Logarithmus des Radikanten geteilt durch den Wurzelexponenten
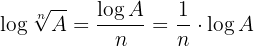
Aus den Regeln  und
und  folgern wir:
folgern wir:

5 Der Logarithmus zur Basis ' ' von '
' von ' ' ist '
' ist ' '
'
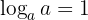
6 Der Logarithmus von  ist
ist  (Die Basis ist nicht von Bedeutung)
(Die Basis ist nicht von Bedeutung)
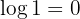
Somit gilt:
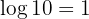
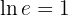
7 Die Logarithmusbasis muss immer größer als null sein
Für  gilt
gilt 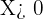
Anwendung der Logarithmusregeln
Basiswechsel
Um einen Logarithmus zur Basis ' ' in einen äquivalenten Ausdruck mit dem Logarithmus zur Basis '
' in einen äquivalenten Ausdruck mit dem Logarithmus zur Basis ' ' umzuschreiben, können wir folgenden Schritt durchführen:
' umzuschreiben, können wir folgenden Schritt durchführen:
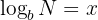
Wir können den Ausdruck wie folgt umwandeln:
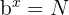
Auf beiden Seiten der Gleichung 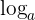 anwenden:
anwenden:
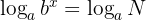
Regel  anwenden und '
anwenden und ' ' bestimmen. Wir erhalten:
' bestimmen. Wir erhalten:
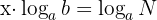

Deshalb:

Beispiel: 
 umwandeln
umwandeln
Wir wenden an: 
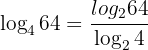
Rechenschritte und Anwendung der Logarithmusregeln zur Lösung eines mathematischen Ausdrucks
Beispiel: Löse 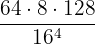 durch die Anwendung der Logarithmusregeln.
durch die Anwendung der Logarithmusregeln.
Wir setzen den zu lösenden Ausdruck mit ' ' gleich:
' gleich:
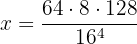
Da alle Zahlen Potenzen von  sind, können wir auf beiden Seiten
sind, können wir auf beiden Seiten  anwenden:
anwenden:

Durch die Anwendung der Logarithmusregeln auf der rechten Seite erhalten wir:
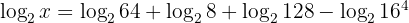
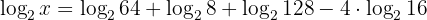
Logarithmen lösen:

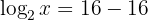
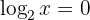
Exponentielle Schreibweise:


Deshalb gilt:
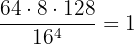
Einen mathematischen Ausdruck mit mehreren Logarithmen so umformen, dass der Ausdruck nur noch einen Logarithmus enthält
Beispiel: Forme den folgenden Ausdruck so um, dass er nur noch einen Logarithmus enthält

Logarithmusregeln anwenden:

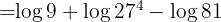

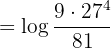
Mit KI zusammenfassen:













Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut