
Logarithmusgleichung
Bei Logarithmusgleichungen steht die Unbekannte in irgendeiner Form in Verbindung mit einem Logarithmus.
Bevor wir eine Logarithmusgleichung lösen, müssen wir die Regeln zum Umgang mit Logarithmen kennen.
Regeln
1 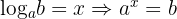
2 
3 
4 
5 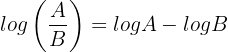
6 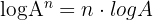
Außerdem müssen wir die Lösungen überprüfen, um zu kontrollieren, dass wir nicht den Logarithmus einer negativen Zahl oder Null erhalten. Dies passiert häufig bei Logarithmen, die einen Ausdruck zweiten Grades enthalten.
Beispiele zur Lösung von Logarithmusgleichungen
Löse die folgenden Logarithmusgleichungen
1 
Um diese Gleichung zu lösen, müssen wir nur Regel  anwenden (Definition des Logarithmus):
anwenden (Definition des Logarithmus):


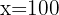
2 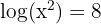
Wir wenden zunächst Regel  an, dann Regel
an, dann Regel  und erhalten so:
und erhalten so:
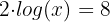
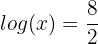
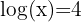
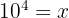

3 
Wir wenden Regel 1 an, danach bestimmen wir die Variable 
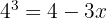

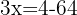
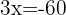
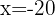
Beim ersten Term wenden wir den Logarithmus eines Produkts an, beim zweiten die Regel vom Logarithmus einer Potenz.
4  Mithilfe der Logarithmusregeln können wir die Logarithmen der Gleichung zusammenfassen. Auf der linken Seite der Gleichung wenden wir Regel
Mithilfe der Logarithmusregeln können wir die Logarithmen der Gleichung zusammenfassen. Auf der linken Seite der Gleichung wenden wir Regel  an, auf der rechten Seite der Gleichung wenden wir Regel
an, auf der rechten Seite der Gleichung wenden wir Regel  an:
an:
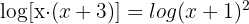
Sobald sich auf jeder Seite der Gleichung nur noch ein Logarithmus befindet, dürfen wir wie folgt gleichsetzen (Numerivergleich):
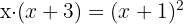
Wir lösen die Gleichung:
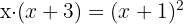
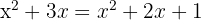
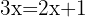

5 
Den Nenner des Bruchs mit der rechten Seite der Gleichung multiplizieren:
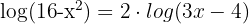
Wir wenden Regel  an und setzen gleich:
an und setzen gleich:

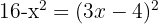
Wir lösen die Gleichung:
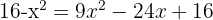

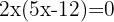

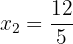
In diesem Fall müssen wir überprüfen, ob eine der Lösungen der Logarithmus einer negativen Zahl ist:
Wir verwenden  :
:
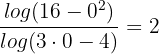
Im Nenner erhalten wir:

Wir erhalten den Logarithmus einer negativen Zahl. Dies stellt eine Scheinlösung dar, da der Logarithmus einer negativen Zahl nicht berechnet werden kann. Deshalb ergibt sich als Lösung für die Gleichung 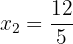 .
.
Mit KI zusammenfassen:













Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut