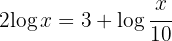
1 Wir wenden auf der rechten Seite die Regel für den Logarithmus eines Quotienten an
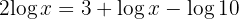
2 Wir subtrahieren  auf beiden Seiten und beachten dabei
auf beiden Seiten und beachten dabei 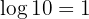 . Wir erhalten:
. Wir erhalten:
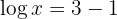
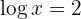
3 Wir beachten die Definition des Logarithmus und dass es sich hier um einen Zehnerlogarithmus handelt:

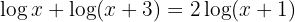
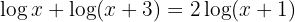
1 Wir wenden auf der linken Seite die Regel für die Summe von Logarithmen an: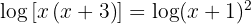
2 Durch den Numerivergleich (oder Gleichsetzen) erhalten wir:

3 Wir lösen die Gleichung und überprüfen die Lösung
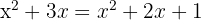



1 Wir wenden auf beiden Seiten die Regel für den Logarithmus einer Potenz an
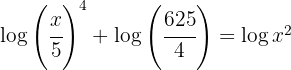
2 Wir wenden die Regel für den Logarithmus eines Produkts an
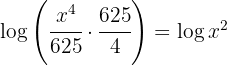
3 Auf der linken Seite rechnen wir

4 Numerivergleich
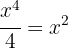
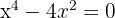
5 Wir lösen die Gleichung
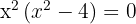
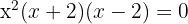

6 Weder  noch
noch  sind Lösungen, da wir beim Einsetzen in die Gleichung den Logarithmus von 0 oder einer negativen Zahl erhalten. Diese Logarithmen existieren nicht. Somit ist
sind Lösungen, da wir beim Einsetzen in die Gleichung den Logarithmus von 0 oder einer negativen Zahl erhalten. Diese Logarithmen existieren nicht. Somit ist  die einzige Lösung
die einzige Lösung
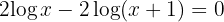
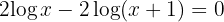
1 Wir bringen 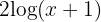 auf die rechte Seite der Gleichung und wenden die Regel einer Potenz auf beiden Seiten der Gleichung an
auf die rechte Seite der Gleichung und wenden die Regel einer Potenz auf beiden Seiten der Gleichung an
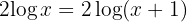

2 Durch den Numerivergleich erhalten wir die Werte für 
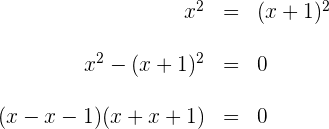
3 Wir lösen den ersten Faktor und erhalten 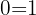 . Dies ist eine unwahre Aussage und bedeutet, dass die Gleichung keine Lösung hat. Beim zweiten Faktor erhalten wir
. Dies ist eine unwahre Aussage und bedeutet, dass die Gleichung keine Lösung hat. Beim zweiten Faktor erhalten wir 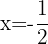 , allerdings ist
, allerdings ist  nicht definiert und bedeutet, dass die Gleichung keine Lösung hat.
nicht definiert und bedeutet, dass die Gleichung keine Lösung hat.


1 Wir lösen den Bruch auf und führen die Substitution durch
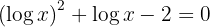
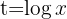
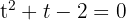
2 Wir lösen die Gleichung
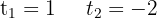
3 Wir führen die Rücksubstitution durch und wenden die Definition des Logarithmus an




1 Wir bringen den zweiten Summanden auf die rechte Seite der Gleichung und wenden die Regel für den Logarithmus einer Potenz an
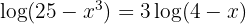

2 Wir wenden den Numerivergleich an und führen die nötigen Rechenschritte durch
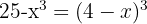
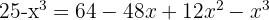
3 Wir lösen die Gleichung mithilfe der a-b-c-Formel

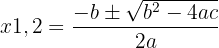
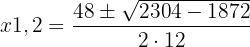
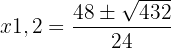

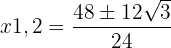
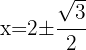


1 Wir multiplizieren beide Seiten der Gleichung mit 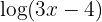
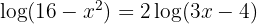
2 Wir wenden auf der rechten Seite die Regel für den Logarithmus einer Potenz an und denken dabei an die Umkehrfunktion von Logarithmen

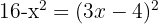
3 Wir lösen die Gleichung.  ist keine Lösung, da wir den Logarithmus einer negativen Zahl im Nenner erhalten, wenn wir den Wert in die Gleichung einsetzen.
ist keine Lösung, da wir den Logarithmus einer negativen Zahl im Nenner erhalten, wenn wir den Wert in die Gleichung einsetzen.

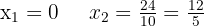
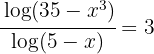
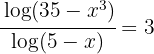
1 Wir formen um
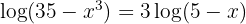
2 Wir wenden auf der rechten Seite die Regel für den Logarithmus einer Potenz an und führen anschließend den Numerivergleich durch

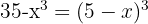
3 Wir führen die nötigen Rechenschritte durch und lösen die quadratische Gleichung


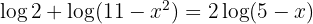
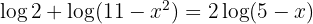
1 Wir wenden auf der linken Seite den Logarithmus eines Produkts an. Auf der rechten Seite wenden wir die Regel für den Logarithmus einer Potenz an.
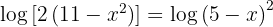
2 Durch den Numerivergleich ergibt sich:
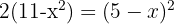
3 Wir lösen die Gleichung und stellen fest, dass wir nicht den Logarithmus von 0 oder einer negativen Zahl erhalten
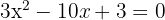



1 Wir multiplizieren beide Seiten der Gleichung mit 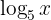 und bringen alle Terme auf die linke Seite
und bringen alle Terme auf die linke Seite
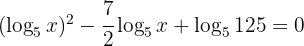
2 Wir beachten, dass  und formen um:
und formen um:
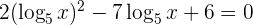
3 Wir führen die Substitution durch
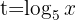
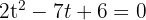
4 Wir lösen die Gleichung
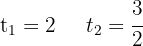
5 Wir führen die Rücksubstitution durch
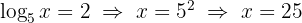

Mit KI zusammenfassen:



Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut