Eine Exponentialfunktion ist eine Gleichung, in der die Variable im Exponenten steht.
Um eine Exponentialgleichung zu lösen, müssen folgende Aspekte beachtet werden:
Eigenschaften der Exponenten
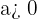
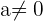
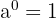
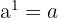
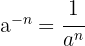
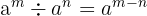
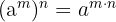
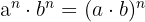
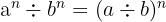
- wenn
, so ist 
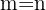
Lösung von Exponentialgleichungen
Fall 1: beide Seiten der Gleichung können auf dieselbe Basis gebracht werden
Führe alle nötigen Rechenschritte durch, um die beiden Seiten der Gleichung auf dieselbe Basis zu bringen und dann die Exponenten gleichzusetzen.
Beispiele
1 
Schreibe die rechte Seite zu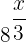 
um und die Zahl 
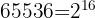zu einer Potenz
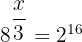
Da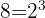 
ist, ist folglich:
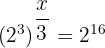
Setze die Potenzen gleich
2
Wandle die Wurzeln in Potenzen mit gebrochenem Exponenten um und setzt die Exponenten gleich
Löse die Gleichung:
3
Klammere den gemeinsamen Faktor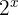 
aus
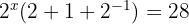
Wende die Vorzeichenregel für negative Potenzen an, vereinfache und klammere 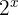aus
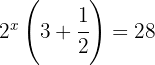
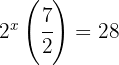
Schreibe die Gleichung um, sodass auf beiden Seiten dieselbe Basis steht und setze die Exponenten gleich
Fall 2: die Summe der Terme einer geometrischen Reihe
Wenn die Summe der 
Terme einer geometrischen Reihe gegeben ist, wende folgende Formel an: inos de una:
Beispiel
Durch Anwenden der Formel für die Summe der Terme einer geometrischen Reihe erhältst du:
Löse nach 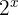auf und bringe beide Seiten der Gleichung auf dieselbe Basis
Fall 3: Umkehrfunktion
Für komplexere Gleichungen lohnt es sich, einen Variablentausch durchzuführen.
Beispiele
1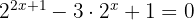 
Um die Summe aus dem Exponenten aufzulösen, wende zuerst die Regel für Potenzprodukte an.
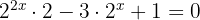
Wende die Regel für Potenzen einer Potenz an
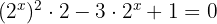
Bilde die Umkehrfunktion für den Variablentausch 
Faktorisiere die Gleichung und löse auf
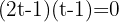
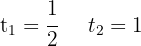
Tausche die Variable zurück
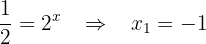
2 
Um die Summe aus dem Exponenten aufzulösen, wende zuerst die Regel für Potenzprodukte oder Quotienten an.
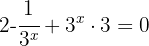
Bilde die Umkehrfunktion für den Variablentausch 
Multipliziere beide Seiten mit 
Faktorisiere und löse die Gleichung
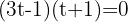
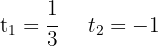
Tausche die Variable zurück
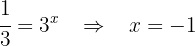
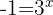
Für die zweite Gleichung erhältst du keine Lösung
3 
Zerlege die Gleichung in die Faktoren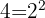 
und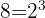
Bilde die Umkehrfunktion
Für das Rückgängig machen der Umkehrfunktion verwende nur das positive Ergebnis.
Da du die Exponenten nicht gleichsetzen kannst, wende den Lograithmus auf beiden Seiten an und gehe nach der Logarithmusregel vor:
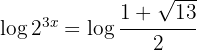
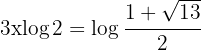
Löse nach 
auf
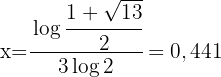
Für die Variante mit negativem Vorzeichen gäbe es keine Lösung, da der Logarithmus einer negativen Zahl nicht existiert.
Fall 4: Die Seiten können nicht auf dieselbe Basis gebracht werden
Um eine Gleichung nach der Variablen aufzulösen, die im Exponenten einer Potenz steht, wird der Logarithmus herangezogen, dessen Basis gleich der Basis der Potenz ist.
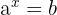
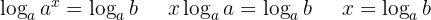
Beispiel
1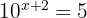 
Bilde auf beiden Seiten den Logarithmus
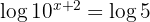
Wende die Logarithmusregel für Potenzen an
Da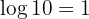 
ist, ist
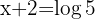
Löse nach auf
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Viel besser kann man es nicht machen.Vielleicht vor jedem Kapitel der schwereren Aufgaben eine Kurzerklärung. Note :sehr gut