Ermittle die Anzahl symmetrischer Zahlen mit acht Ziffern. Wie viele neunstellige symmetrische Zahlen gibt es?
Wir stellen fest, dass die Zahl im 1. Fall folgende Form hat: 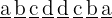
Der Wert von  kann nicht 0 sein. Somit haben wir
kann nicht 0 sein. Somit haben wir  mögliche Werte für den ersten Term. Für
mögliche Werte für den ersten Term. Für  ,
,  und
und  gilt, dass sie jede Zahl zwischen
gilt, dass sie jede Zahl zwischen  und
und  sein können.
sein können.
Durch Multiplikation ergibt sich schließlich, dass die Anzahl der achtstelligen symmetrischen Zahlen 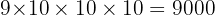 ist.
ist.
Ähnlich wie im vorherigen Fall hat die Zahl mit  Ziffern die Form
Ziffern die Form 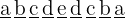
Auch hier kann die erste Ziffer nicht 0sein, so dass wir  Möglichkeiten für die erste Stelle haben. Und für die möglichen Werte, die
Möglichkeiten für die erste Stelle haben. Und für die möglichen Werte, die  ,
,  ,
,  und
und  annehmen können, haben wir
annehmen können, haben wir  Möglichkeiten. Multipliziert man die Anzahl der möglichen Werte für jede der Positionen, erhalten wir
Möglichkeiten. Multipliziert man die Anzahl der möglichen Werte für jede der Positionen, erhalten wir 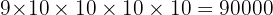 symmetrische Zahlen mit 9 Ziffern.
symmetrische Zahlen mit 9 Ziffern.
Vier verschiedene Mathematikbücher, sechs verschiedene Physikbücher und zwei verschiedene Chemiebücher stehen in einem Regal. Auf wie viele verschiedene Arten können sie angeordnet werden, wenn:
1Die Bücher der einzelnen Fächer müssen alle zusammen stehen. Da die Bücher der einzelnen Fächer zusammengehören und jedes Buch anders ist, können wir zunächst die Anzahl der Permutationen in Mathematik, Physik und Chemie getrennt berechnen. Wir haben also jeweils 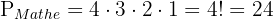
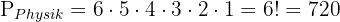
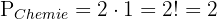 Da wir drei verschiedene Fächer haben, könnte ein Chemie- oder Mathematikbuch zuerst kommen und dann ein Physikbuch, oder zuerst ein Physikbuch und dann ein Chemiebuch. Die Gesamtzahl der Permutationen dieses Typs ist
Da wir drei verschiedene Fächer haben, könnte ein Chemie- oder Mathematikbuch zuerst kommen und dann ein Physikbuch, oder zuerst ein Physikbuch und dann ein Chemiebuch. Die Gesamtzahl der Permutationen dieses Typs ist  . Durch Multiplikation ergibt sich schließlich die folgende Anzahl von Möglichkeiten, die Bücher zu platzieren:
. Durch Multiplikation ergibt sich schließlich die folgende Anzahl von Möglichkeiten, die Bücher zu platzieren: 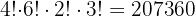
2 Nur Mathematikbücher sollten zusammen stehen. Jetzt haben wir nur noch zwei Schulfächer, die Mathebücher und den Rest. Insgesamt bleiben  Bücher übrig, so dass die Gesamtzahl der Permutationen für den Rest des Buches
Bücher übrig, so dass die Gesamtzahl der Permutationen für den Rest des Buches 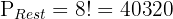 ist. Da ein Mathematik-, Chemie- oder Physikbuch durchaus an erster Stelle stehen kann, müssen wir das Produkt aus
ist. Da ein Mathematik-, Chemie- oder Physikbuch durchaus an erster Stelle stehen kann, müssen wir das Produkt aus 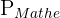 und
und 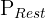 mit
mit  multiplizieren, um das Endergebnis zu erhalten:
multiplizieren, um das Endergebnis zu erhalten:
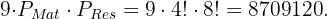
Eine Person hat fünf Münzen mit unterschiedlichem Wert. Wie viele verschiedene Geldbeträge kann sie mit den fünf Münzen bilden?
Man kann zunächst zählen, wie viele Geldbeträge man erhält, wenn man nur eine Münze verwendet, dann zwei, dann drei, dann vier und schließlich fünf. Dazu nehmen wir die Anzahl der Kombinationen von eins zu fünf, zwei zu fünf, drei zu fünf und so weiter. Wenn wir am Ende zusammenzählen, erhalten wir unser Ergebnis: 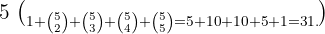
5 rote Kugeln, 2 weiße Kugeln und 3 blaue Kugeln sind in einer Reihe angeordnet. Wenn die Kugeln der gleichen Farbe nicht voneinander unterschieden werden, auf wie viele Arten können sie dann angeordnet werden?
In diesem Fall haben wir eine Permutation mit Wiederholung, da Kugeln der gleichen Farbe nicht zu unterscheiden sind. Mithilfe des Multiplikationsprinzips erhalten wir eine Formel zur Lösung dieses Problems: 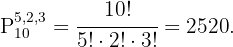
Löse die kombinatorischen Gleichungen:

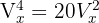
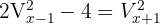

Beachte, dass  und
und 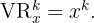
1


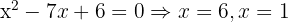
Wir nehmen die Lösung 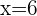 .
.
2
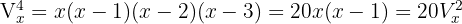

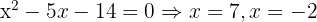
Wir nehmen die Lösung  .
.
3
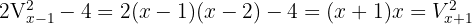
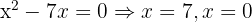
Wir nehmen die Lösung  .
.
4

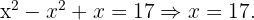
Löse die kombinatorischen Gleichungen:
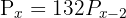
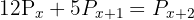
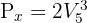
Beachte, dass 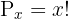 und
und 
1
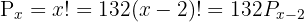

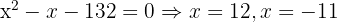
Wir nehmen die Lösung 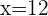 .
.
2
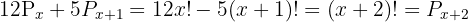
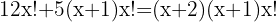
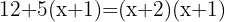
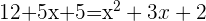
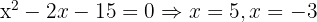
Wir nehmen die Lösung  .
.
3


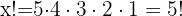
Somit ist  .
.
Löse die kombinatorischen Gleichungen:
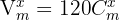


Beachte, dass 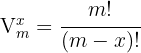 y
y 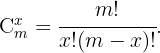
1
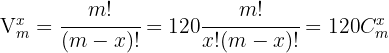

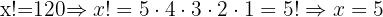
2
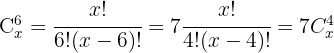
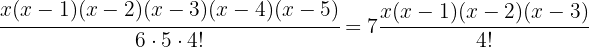

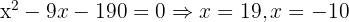
Wir nehmen die Lösung  .
.
3
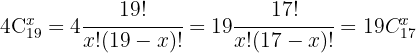
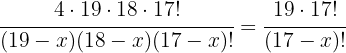

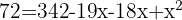
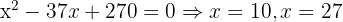
Wir nehmen die Lösung 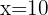 .
.
 ist keine Lösung, weil die Anzahl der Reihenfolgen in den Kombinationen kleiner ist als die Anzahl der Elemente.
ist keine Lösung, weil die Anzahl der Reihenfolgen in den Kombinationen kleiner ist als die Anzahl der Elemente.
Löse die kombinatorischen Gleichungen:
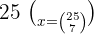
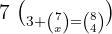
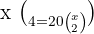
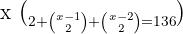
1
Für diese erste Aufgabe wenden wir das 1. Gesetz kombinatorischer Zahlen an. Dieses besagt, dass 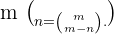 Somit:
Somit: 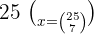 impliziert, dass
impliziert, dass 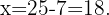
2
Für diese Aufgabe wenden wir das 2. Gesetz kombinatorischer Zahlen an. Dieses besagt, dass  Somit:
Somit: 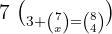 impliziert, dass
impliziert, dass 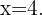
3
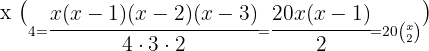
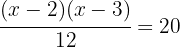
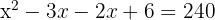

Wir nehmen die Lösung 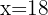 .
.
4
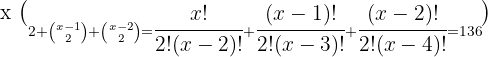
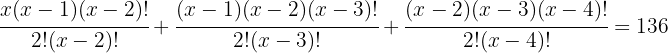
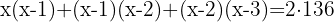
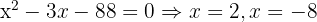
Wir nehmen die Lösung  .
.
Mit KI zusammenfassen:


