Variationen
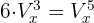
Wir haben die kombinatorische Gleichung
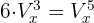
Wir wenden die Formel einer Variation an
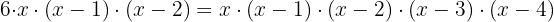
Wir bearbeiten die Gleichung
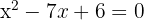
Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten
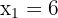
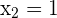
Wir verwerfen jedoch die zweite Lösung, da  größer oder gleich
größer oder gleich  und
und  sein muss. Somit ist die Lösung
sein muss. Somit ist die Lösung
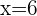
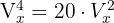
Wir haben die kombinatorische Gleichung
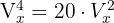
Wir wenden die Formel einer Variation an
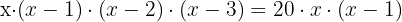
Wir bearbeiten die Gleichung
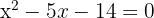
Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten
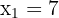
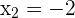
Wir verwerfen jedoch die zweite Lösung, weil  nicht negativ sein kann. Somit ist die Lösung
nicht negativ sein kann. Somit ist die Lösung


Wir haben die kombinatorische Gleichung

Wir wenden die Formel einer Variation an

Wir bearbeiten die Gleichung
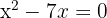
Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten
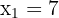

Wir verwerfen jedoch die zweite Lösung, da  nicht gleich
nicht gleich  oder negativ sein kann. Somit ist die Lösung
oder negativ sein kann. Somit ist die Lösung

Variationen mit und ohne Wiederholung

Wir haben die kombinatorische Gleichung

Wir wenden die Formel einer Variation und einer Variation mit Wiederholung an
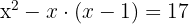
Wir bearbeiten die Gleichung
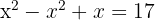
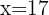
Permutationen
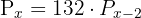
Wir haben die kombinatorische Gleichung
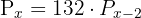
Wir wenden die Formel einer Permutation an
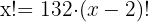
Wir bearbeiten die Gleichung
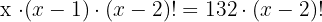
Da auf beiden Seiten mit einem Faktor  multipliziert wird, streichen wir ihn
multipliziert wird, streichen wir ihn

Wir berechnen
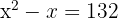
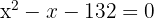
Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten
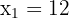
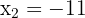
Wir verwerfen jedoch die zweite Lösung, weil  nicht negativ sein kann. Somit ist die Lösung
nicht negativ sein kann. Somit ist die Lösung
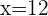

Wir haben die kombinatorische Gleichung

Wir wenden die Formel einer Permutation an
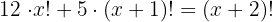
Wir bearbeiten die Gleichung und streichen den gemeinsamen Faktor

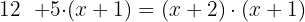
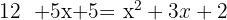
Wir bringen alle Terme auf eine Seite und addieren wie folgt
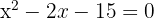
Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten
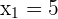
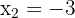
Wir verwerfen jedoch die zweite Lösung, weil  nicht negativ sein kann. Somit ist die Lösung
nicht negativ sein kann. Somit ist die Lösung

Variationen und Permutationen
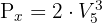
Wir haben die kombinatorische Gleichung
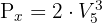
Wir wenden die Formel für eine Permutation und für eine Variation an
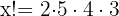
Wir ordnen die Faktoren um und fügen  hinzu
hinzu
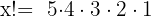

Daraus schließen wir, dass

Variationen und Kombinationen
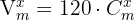
Wir haben die kombinatorische Gleichung
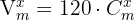
Wir wenden die Formel einer Variation und einer Kombination an
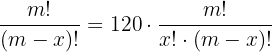
Wir streichen die gemeinsamen Faktoren auf beiden Seiten der Gleichung
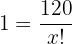
Dies ist äquivalent zu
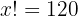


Daraus schließen wir, dass

Kombinationen

Wir haben die kombinatorische Gleichung

Wir wenden die Formel einer Kombination an
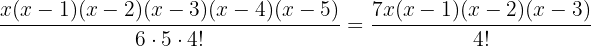
Wir streichen die gemeinsamen Faktoren auf beiden Seiten der Gleichung

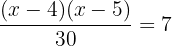
Wir berechnen



Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten
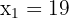

Wir verwerfen jedoch die zweite Lösung, weil  nicht negativ sein kann. Somit ist die Lösung
nicht negativ sein kann. Somit ist die Lösung

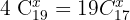
Wir haben die kombinatorische Gleichung
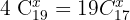
Wir wenden die Formel einer Kombination an

Wir bearbeiten die Gleichung und streichen gemeinsame Faktoren
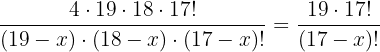

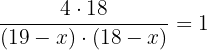
Wir beseitigen den Nenner und multiplizieren aus
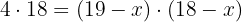
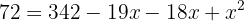
Wir vereinfachen und bringen alle Terme auf eine Seite
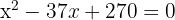
Wir wenden die allgemeine Formel oder Faktorisierung an, um die Lösungen der Gleichung zweiten Grades zu erhalten


Wir verwerfen jedoch die zweite Lösung, weil die Ordnungszahl in den Kombinationen kleiner ist als die Anzahl der Elemente, d. h.  muss kleiner sein als
muss kleiner sein als  . Somit ist die Lösung
. Somit ist die Lösung
Mit KI zusammenfassen:


