In diesem Artikel stellen wir verschiedene Wahrscheinlichkeitsaufgaben vor, die mit Hilfe des bekannten Satz von Bayes gelöst werden. Bevor wir jedoch zu den Aufgaben kommen, wollen wir uns noch einmal ins Gedächtnis rufen, was der Satz von Bayes besagt.
Satz von Bayes:  seien sich gegenseitige ausschließende Ereignisse, deren Vereinigung der Ergebnisraum
seien sich gegenseitige ausschließende Ereignisse, deren Vereinigung der Ergebnisraum  ist, das heißt
ist, das heißt
Wenn  ein weiteres Ereignis ist, gilt
ein weiteres Ereignis ist, gilt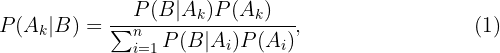 ,
,
wobei 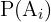 die Wahrscheinlichkeit des Ereignisses
die Wahrscheinlichkeit des Ereignisses  ist, genannt A-priori-Wahrscheinlichkeit.
ist, genannt A-priori-Wahrscheinlichkeit. 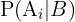 stellt die Wahrscheinlichkeit des Ereignisses
stellt die Wahrscheinlichkeit des Ereignisses  unter der Voraussetzung des Ereignisses
unter der Voraussetzung des Ereignisses  dar, auch bekannt als A-posteriori-Wahrscheinlichkeit.
dar, auch bekannt als A-posteriori-Wahrscheinlichkeit.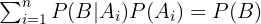 ist die totale Wahrscheinlichkeit des Ereignisses
ist die totale Wahrscheinlichkeit des Ereignisses 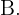 Die Gleichung (1) wird Satz von Bayes gennant.
Die Gleichung (1) wird Satz von Bayes gennant.
Aufgaben mit Lösungen
Es gibt zwei Urnen. Urne 1 enthält 4 weiße Umschläge und 6 schwarze Umschläge. Urne 2 enthält 4 weiße Umschläge und 2 schwarze Umschläge. Wenn man zufällig einen Umschlag aus einer der beiden Urnen zieht und weiß, dass der Umschlag schwarz ist, wie hoch ist dann die Wahrscheinlichkeit, dass der Umschlag aus Urne 1 stammt?
Wir sehen uns die folgenden Ereignisse mit ihren jeweiligen Wahrscheinlichkeiten an:
 "Urne 1 wird gewählt"
"Urne 1 wird gewählt" 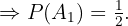
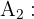 "Urne 2 wird gewählt"
"Urne 2 wird gewählt" 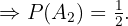
Wir sehen und außerdem das Ereignis  an: "Es wird ein schwarzer Umschlag gezogen".
an: "Es wird ein schwarzer Umschlag gezogen".
Die Hypothesen des Problems zeigen uns, dass:
Die Wahrscheinlichkeit, einen schwarzen Umschlag aus Urne 1 zu ziehen, beträgt 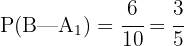 , da sich in der Urne insgesamt 10 Umschläge befinden, von denen 6 schwarz sind.
, da sich in der Urne insgesamt 10 Umschläge befinden, von denen 6 schwarz sind.
Die Wahrscheinlichkeit, einen schwarzen Umschlag aus Urne 2 zu ziehen, beträgt 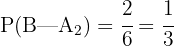 , da sich in der Urne insgesamt 6 Umschläge befinden, von denen 2 schwarz sind.
, da sich in der Urne insgesamt 6 Umschläge befinden, von denen 2 schwarz sind.
Daher möchten wir 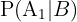 herausfinden, d. h. die Wahrscheinlichkeit, dass der schwarze Umschlag aus Urne 1 gezogen wurde.
herausfinden, d. h. die Wahrscheinlichkeit, dass der schwarze Umschlag aus Urne 1 gezogen wurde.
Unter Verwenung des Satzes von Bayes erhalten wir
Ein Mann ist dafür bekannt, dass er in zwei von drei Fällen die Wahrheit sagt. Er wirft eine Münze und sagt, dass sie auf der Kopfseite gelandet ist. Berechne die Wahrscheinlichkeit, dass die Münze tatsächlich auf der Kopfseite gelandet ist.
Wir sehen uns die folgenden Ereignisse mit ihren jeweiligen Wahrscheinlichkeiten an:
 "Die Münze zeigt Kopf"
"Die Münze zeigt Kopf" 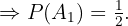
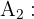 "Die Münze zeigt Zahl"
"Die Münze zeigt Zahl" 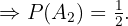
Wir sehen und außerdem das Ereignis  an: " Der Mann sagt voraus, dass Kopf geworfen wird".
an: " Der Mann sagt voraus, dass Kopf geworfen wird".
Die Hypothesen des Problems zeigen uns, dass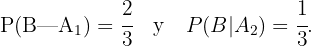
Wir möchten 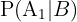 herausfinden, das heißt, die Wahrscheinlichkeit, dass Kopf geworfen wurde, so wie es der Mann vorausgesagt hatte. Unter Verwenung des Satzes von Bayes erhalten wir
herausfinden, das heißt, die Wahrscheinlichkeit, dass Kopf geworfen wurde, so wie es der Mann vorausgesagt hatte. Unter Verwenung des Satzes von Bayes erhalten wir

Wenn du lieber von zu Hause aus lernst, könnte dich unser Online-Matheunterricht interessieren.
Bei einer Multiple-Choice-Prüfung beträgt die Wahrscheinlichkeit, die Antwort zu wissen,  . Bei
. Bei  Antwortmöglichkeiten beträgt die Wahrscheinlichkeit, ohne Wissen die richtige Antwort zu wählen,
Antwortmöglichkeiten beträgt die Wahrscheinlichkeit, ohne Wissen die richtige Antwort zu wählen, 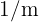 . Angenommen, ein Schüler hat eine richtige Antwort gegeben, wie hoch ist dann die Wahrscheinlichkeit, dass er die Antwort tatsächlich wusste?
. Angenommen, ein Schüler hat eine richtige Antwort gegeben, wie hoch ist dann die Wahrscheinlichkeit, dass er die Antwort tatsächlich wusste?
Wir sehen uns die folgenden Ereignisse mit ihren jeweiligen Wahrscheinlichkeiten an:
 "Der Schüler weiß die Antwort"
"Der Schüler weiß die Antwort" 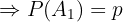
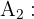 "Der Schüler weiß die Antwort nicht"
"Der Schüler weiß die Antwort nicht" 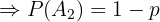
Wir sehen und außerdem das Ereignis  an: "Der Schüler antwortet richtig".
an: "Der Schüler antwortet richtig".
Die Hypothesen des Problems zeigen uns, dass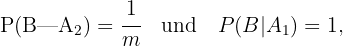
wobei wir bei der zweiten Wahrscheinlichkeit annehmen, dass der Schüler die Antwort weiß und somit auch richtig antwortet.
Wir möchten 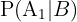 herausfinden, das heißt, die Wahrscheinlichkeit, dass der Schüler die Antwort wusste, da er richtig geantwortet hat. Unter Verwenung des Satzes von Bayes erhalten wir
herausfinden, das heißt, die Wahrscheinlichkeit, dass der Schüler die Antwort wusste, da er richtig geantwortet hat. Unter Verwenung des Satzes von Bayes erhalten wir
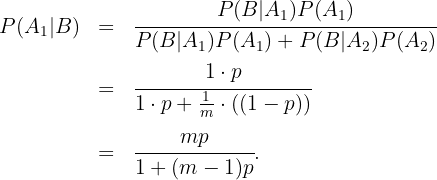
Wenn zum Beispiel 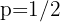 und
und 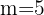 , erhalten wir
, erhalten wir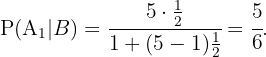
Ein Paar hat zwei Kinder, von denen eines weiblich ist und Christina heißt. Wenn der Anteil der Frauen mit dem Namen „Christina” weltweit 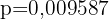 beträgt, wie hoch ist dann die Wahrscheinlichkeit, dass das Paar zwei Töchter hat?
beträgt, wie hoch ist dann die Wahrscheinlichkeit, dass das Paar zwei Töchter hat?
Wir sehen uns die folgenden Ereignisse mit ihren jeweiligen Wahrscheinlichkeiten an:
 "Das Paar hat zwei Töchter"
"Das Paar hat zwei Töchter"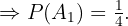
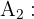 "Das Paar hat eine Tochter und einen Sohn"
"Das Paar hat eine Tochter und einen Sohn" 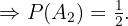
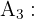 "Das Paar hat zwei Söhne"
"Das Paar hat zwei Söhne" 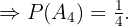
Die oben genannten Wahrscheinlichkeiten lassen sich direkt berechnen, wenn man davon ausgeht, dass die vier Möglichkeiten (zwei Töchter, eine Tochter und ein Sohn, ein Sohn und eine Tochter sowie zwei Söhne) jeweils eine Wahrscheinlichkeit von 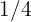 haben und die beiden mittleren Möglichkeiten im Ereignis
haben und die beiden mittleren Möglichkeiten im Ereignis 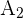 enthalten sind, was ihre Wahrscheinlichkeit von
enthalten sind, was ihre Wahrscheinlichkeit von  rechtfertigt.
rechtfertigt.
Wir sehen und außerdem das Ereignis  an: "Eine Tochter, die Christina heißt". Die Hypothesen des Problems zeigen uns, dass
an: "Eine Tochter, die Christina heißt". Die Hypothesen des Problems zeigen uns, dass 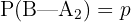
und somit auch 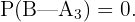 Ebenso erhalten wir, dass
Ebenso erhalten wir, dass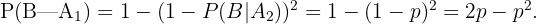
Wir möchten 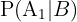 herausfinden, das heißt, die Wahrscheinlichkeit, dass das Paar 2 Töchter hat, wenn wir a-priori wissen, dass eine von ihnen Christina heißt. Unter Verwenung des Satzes von Bayes erhalten wir
herausfinden, das heißt, die Wahrscheinlichkeit, dass das Paar 2 Töchter hat, wenn wir a-priori wissen, dass eine von ihnen Christina heißt. Unter Verwenung des Satzes von Bayes erhalten wir
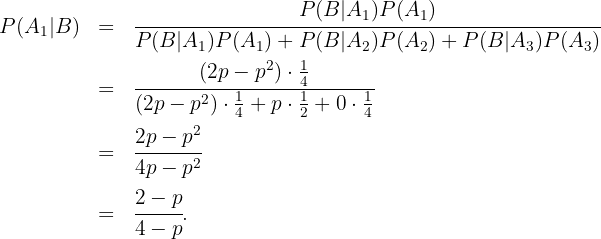
Wir setzen 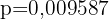 ein und erhalten
ein und erhalten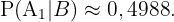
Mit KI zusammenfassen:



