Kapitel

Ergebnisraum
Bei der Wahrscheinlichkeitsrechnung ist der el Ergebnisraum, notiert mit 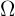 (oder auch mit
(oder auch mit  ), die Menge aller möglichen Ergebnisse bei der Durchführung eines Zufallsexperiments.
), die Menge aller möglichen Ergebnisse bei der Durchführung eines Zufallsexperiments.
Beispiel
1 Würfeln
Nehmen wir das Experiment, bei dem ein Würfel geworfen wird. Wir wissen, dass der Würfel 6 Seiten hat, wobei jede Seite eine andere ganzzahlige Zahl hat, die von  bis
bis 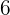
 gehen. Unser Ergebnisraum mit allen möglichen Ergebnissen, die wir beim Würfeln erzielen können, wäre also
gehen. Unser Ergebnisraum mit allen möglichen Ergebnissen, die wir beim Würfeln erzielen können, wäre also
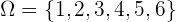
2 Werfen von 2 Münzen
Nehmen wir das Experiment des Werfens zweier Münzen. Eine Münze hat nur zwei Seiten, nämlich Kopf ( ) oder Zahl (
) oder Zahl (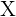 ). Da wir zwei Münzen werfen, wären unsere Ergebnisse Paare, d. h. unser Ergebnisraum mit allen möglichen Ergebnissen, die wir erhalten könnten, wäre
). Da wir zwei Münzen werfen, wären unsere Ergebnisse Paare, d. h. unser Ergebnisraum mit allen möglichen Ergebnissen, die wir erhalten könnten, wäre
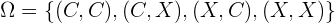
Ein weiteres wichtiges Konzept ist das Ereignis, notiert mit  . Ein Ereignis ist eine Teilmenge des Ergebnisraums, oder weniger formell, das Eintreten "bestimmter Fälle".
. Ein Ereignis ist eine Teilmenge des Ergebnisraums, oder weniger formell, das Eintreten "bestimmter Fälle".
Beispiel:
Die Tatsache, dass beim Würfeln eine 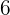 oder eine
oder eine 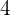 gewürfelt wird, wäre durch folgende Teilmenge gegeben
gewürfelt wird, wäre durch folgende Teilmenge gegeben
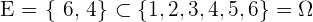
Ein Elementarereignis ist ein Ereignis, das aus nur einem Element besteht, nämlich  . Mit anderen Worten, es handelt sich um ein Ereignis, bei dem nur ein Ergebnis in Betracht kommt.
. Mit anderen Worten, es handelt sich um ein Ereignis, bei dem nur ein Ergebnis in Betracht kommt.
Beispiel:
Die Tatsache, dass beim einmaligen, gleichzeitigen Werfen zweier Münzen beide Münzen Kopf 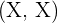 zeigen, ist ein Elementarereignis und durch folgende Teilmenge gegeben
zeigen, ist ein Elementarereignis und durch folgende Teilmenge gegeben

Wir erinnern uns daran, dass jedes Paar, zum Beispiel 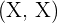 , ein einziges Ergebnis ist, obwohl es aus zwei einzelnen Elementen besteht (da wir zwei unterschiedliche Münzen werfen).
, ein einziges Ergebnis ist, obwohl es aus zwei einzelnen Elementen besteht (da wir zwei unterschiedliche Münzen werfen).
Gleichwahrscheinliche Ereignisse
In manchen Fällen betrachtet die Wahrscheinlichkeitsrechnung die verschiedenen Ergebnisse eines Experiments als gleichwahrscheinlich. In diesen Fällen wird in einem Ergebnisraum mit 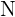 möglichen Ergebnissen mit der gleichen Eintrittswahrscheinlichkeit jedem Ergebnis die Wahrscheinlichkeit von
möglichen Ergebnissen mit der gleichen Eintrittswahrscheinlichkeit jedem Ergebnis die Wahrscheinlichkeit von 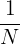 zugeordnet.
zugeordnet.
In einem Ergebnisraum mit gleichwahrscheinlichen Ergebnissen lässt sich die Wahrscheinlichkeit des Eintretens eines Ereignisses leicht berechnen:
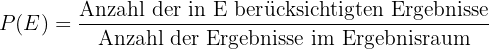
Vereinigung von Ereignissen
Gegeben sind zwei Ereignisse  und
und  . Die Vereinigung von Ereignissen,
. Die Vereinigung von Ereignissen,  , ist das Ereignis, dass alle Elemente bilden, die zu
, ist das Ereignis, dass alle Elemente bilden, die zu  oder
oder  gehören. Das Ereignis
gehören. Das Ereignis  tritt ein, wenn eines von beiden,
tritt ein, wenn eines von beiden,  oder
oder  , oder beide entreten.
, oder beide entreten.
 wird als "
wird als " vereinigt mit
vereinigt mit  " gelesen.
" gelesen.
Beobachtung. In Wirklichkeit ist die Vereinigung von zwei Ereignissen nichts anderes als die Vereinigung ihrer Mengen.
Beispiel:
Wir nehmen ein Experiment, bei dem ein Würfel geworfen wird und sehen uns folgendes Ereignis an: Es wird eine gerade Zahl wie  gewürfelt und eine Zahl, die ein Vielfaches von drei ist, nämlich
gewürfelt und eine Zahl, die ein Vielfaches von drei ist, nämlich  . Wir berechnen die Vereinigung der Ereignisse
. Wir berechnen die Vereinigung der Ereignisse  und
und  (
( ):
):



Regeln für die Vereinigung von Ereignissen
- KommutativitätGegeben sind zwei Ereignisse
 und
und  . Es gilt:
. Es gilt: .
. - AssoziativitätGegeben sind die Ereignisse
 ,
,  und
und  . Es gilt:
. Es gilt: .
. - IdempotenzFür das Ereignis
 gilt:
gilt: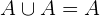 .
. - DistributivitätGegeben sind die Ereignisse
 ,
,  und
und  . Es gilt:
. Es gilt: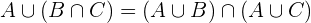 und
und
- VereinfachungGegeben sind zwei Ereignisse
 und
und  . Es gilt:
. Es gilt: .
.
- Neutrales ElementFür das Ereignis
 gilt:
gilt: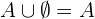 .
.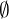 ist hierbei das unmögliche Ereignis.
ist hierbei das unmögliche Ereignis. - Absorption
 ist ein beliebiges Ereignis und
ist ein beliebiges Ereignis und 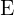 ein beliebiges anderes größeres Ereignis, das das Ereignis
ein beliebiges anderes größeres Ereignis, das das Ereignis  enthält (es kann sogar derselbe Ergebnisraum [
enthält (es kann sogar derselbe Ergebnisraum [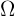 sein). Somit gilt
sein). Somit gilt .
.
Wahrscheinlichkeit der Vereinigung von Ereignissen
Wir nehmen zwei Ereignisse  und
und  mit den jeweiligen Wahrscheinlichkeiten
mit den jeweiligen Wahrscheinlichkeiten  und
und  . Somit ist die Wahrscheinlichkeit ihrer Vereinigung
. Somit ist die Wahrscheinlichkeit ihrer Vereinigung  gegeben durch
gegeben durch
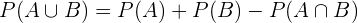
Daraus ergeben sich zwei wichtige Fälle.  und
und  .
.
Wahrscheinlichkeit von vereinbaren Ereignissen
Wir sagen, dass zwei Ereignisse  und
und  vereinbar sind, wenn sie mindestens ein gemeinsames Elementarereignis enthalten. Mit anderen Worten, wenn beide mindestens ein gemeinsames Ergebnis in Betracht ziehen.
vereinbar sind, wenn sie mindestens ein gemeinsames Elementarereignis enthalten. Mit anderen Worten, wenn beide mindestens ein gemeinsames Ergebnis in Betracht ziehen.
Wenn zwei Ereignisse  und
und  vereinbar sind, ist ihre Schnittmenge nicht leer (unterscheidet sich von der leeren Menge
vereinbar sind, ist ihre Schnittmenge nicht leer (unterscheidet sich von der leeren Menge  ). Das heißt
). Das heißt
 .
.
Da die Schnittmenge in diesem Fall nicht leer ist und ihre Elemente zum Ergebinsraum gehören, gilt  . Somit nehmen wir die Gleichung (\ref{ProbabilidadUnion}), um die Wahrscheinlichkeit von
. Somit nehmen wir die Gleichung (\ref{ProbabilidadUnion}), um die Wahrscheinlichkeit von  zu berechnen.
zu berechnen.
 .
.
Beispiel
Wir nehmen ein Experiment, bei dem ein Würfel geworfen wird und die folgenden Ereignisse:
- Die gewürfelte Zahl ist ein Vielfaches von drei:

- Beim Würfeln erscheint die Zahl
 :
:  .
.
Wir stellen fest, dass  . Die Mengen sind also vereinbar. Außerdem gilt
. Die Mengen sind also vereinbar. Außerdem gilt 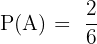 und
und 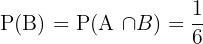 . Wir wenden die Formel der Gleichung (\ref{ProbabilidadUnion}) an und erhalten
. Wir wenden die Formel der Gleichung (\ref{ProbabilidadUnion}) an und erhalten
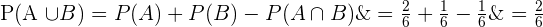
Wahrscheinlichkeit der Vereingung von unvereinbaren Ereignissen
Zwei Ereignisse  und
und  sind unvereinbar, wenn sie kein gemeinsames Element haben. Mit anderen Worten, wenn ein Ergebnis, das in
sind unvereinbar, wenn sie kein gemeinsames Element haben. Mit anderen Worten, wenn ein Ergebnis, das in  enthalten ist, nicht in
enthalten ist, nicht in  enthalten ist und umgekehrt.
enthalten ist und umgekehrt.
Zwei Ereignisse  und
und  sind außerdem unvereinbar, wenn ihre Schnittmenge leer ist (leere Menge
sind außerdem unvereinbar, wenn ihre Schnittmenge leer ist (leere Menge  ). Das heißt
). Das heißt
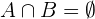
Die Wahrscheinlichkeit der leeren Menge ist  , das dieses Ereignis in keinem Ergebnis vorkommt. Daher lautet die Gleichung wie folgt:
, das dieses Ereignis in keinem Ergebnis vorkommt. Daher lautet die Gleichung wie folgt:
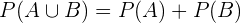
Beispiel
Wir nehmen ein Experiment, bei dem ein Würfel geworfen wird und die folgenden Ereignisse:
- Beim Würfeln erscheint eine Primzahl kleiner als 4:

- Beim Würfeln erscheint die Zahl
 oder die Zahl
oder die Zahl  :
:  .
.
Wir stellen fest, dass  . Die Mengen sind also unvereinbar. Außerdem haben wir
. Die Mengen sind also unvereinbar. Außerdem haben wir 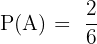 und
und 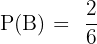 . Wir wenden die Formel der Gleichung (\ref{ProbabilidadIncompatibles}) an und erhalten
. Wir wenden die Formel der Gleichung (\ref{ProbabilidadIncompatibles}) an und erhalten
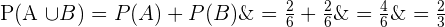
Mit KI zusammenfassen:












