Kapitel

Laplace-Experiment
Dieses Experiment gibt die Wahrscheinlichkeit an, dass ein Ereignis eintritt oder dass man bei einem Glücksspiel gewinnt.
Wenn wir einen Würfel werfen, muss berücksichtigt werden, dass die Wahrscheinlichkeit, dass eine der Seiten mit den Zahlen 1 bis 6 erscheint, gleich groß ist, so dass die Wahrscheinlichkeit, dass eine Zahl erscheint,  ist.
ist.
Wenn wir nun wissen wollen, wie hoch die Wahrscheinlichkeit für eine gerade Zahl ist, wäre das Ergebnis 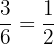 , denn
, denn 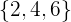 sind die geraden Ergebnisse.
sind die geraden Ergebnisse.
Im Allgemeinen ist die Wahrscheinlichkeit eines Ereignisses das Verhältnis zwischen der Anzahl der günstigen Fälle und der Gesamtzahl der möglichen Fälle, was dem Laplace-Experiment entspricht.
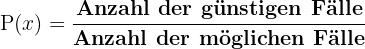
Unvereinbare Ereignisse
Dies sind zwei Ereignisse, die nicht gleichzeitig eintreten können.
Beispiel:
Es wird eine Umfrage unter Universitätsstudenten durchgeführt, um festzustellen, wie viele von ihnen rauchen und wie viele nicht, sodass  die Menge der Raucher und
die Menge der Raucher und  die der Nichtraucher ist:
die der Nichtraucher ist:
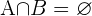
Denn eine Person kann nicht gleichzeitig Raucher und Nichtraucher sein.
Wenn also ein Schüler oder eine Schülerin zufällig ausgewählt wird, möchten wir wissen, wie hoch die Wahrscheinlichkeit ist, dass er oder sie raucht oder nicht raucht, und verwenden folgende Formel:
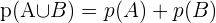
Vereinbare Ereignisse
Dies sind zwei Ereignisse, die gleichzeitig auftreten können.
Beispiel:
An einer Universität gibt es Student:innen, die Englisch, Französisch oder beide Sprachen studieren. Wenn  diejenigen sind, die Englisch studieren, und
diejenigen sind, die Englisch studieren, und  diejenigen, die Französisch studieren, dann sind
diejenigen, die Französisch studieren, dann sind 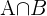 diejenigen, die Englisch und Französisch studieren. Somit:
diejenigen, die Englisch und Französisch studieren. Somit:
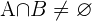
Wenn wir nun einen Studenten oder eine Studentin nach dem Zufallsprinzip auswählen und wissen wollen, wie hoch die Wahrscheinlichkeit ist, dass er/sie Englisch oder Französisch studiert, verwenden wir die folgende Formel: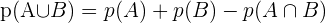
Bedingte Wahrscheinlichkeit
Wenn die Wahrscheinlichkeit eines Ereignisses  durch ein anderes Ereignis
durch ein anderes Ereignis  beeinflusst werden kann.
beeinflusst werden kann.
Beispiel:
Stell dir vor, du spielst mit einer anderen Person ein Spiel, bei dem du dreimal eine Münze wirfst. Du gewinnst, wenn sie Kopf zeigt, und verlierst, wenn sie Zahl zeigt. Um zu gewinnen, musst du mindestens zwei von drei Würfen gewinnen.
Wenn wir mit 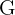 einen gewonnenen Wurf und mit
einen gewonnenen Wurf und mit  einen verlorenen Wurf darstellen, dann wären die Ergebnisse
einen verlorenen Wurf darstellen, dann wären die Ergebnisse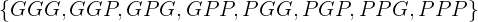 .
.
Um zu gewinnen, muss 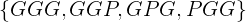 auftreten. Deshalb ist die Wahrscheinlichkeit, zu gewinnen,
auftreten. Deshalb ist die Wahrscheinlichkeit, zu gewinnen, 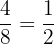 .
.
Angenommen, der erste Wurf gelingt nicht, sodass noch zwei Würfe verbleiben. Wie hoch ist die Wahrscheinlichkeit, zu gewinnen?
Wir verwenden die Formel:
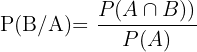
Wir nennen  das Ereignis, den 1. Wurf zu gewinnen und
das Ereignis, den 1. Wurf zu gewinnen und  das Ereignis, zu verlieren. Die Ergebnisse wären
das Ereignis, zu verlieren. Die Ergebnisse wären 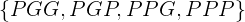 . Somit wäre
. Somit wäre 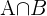 das Ereignis, den 1. Wurf zu gewinnen und zu verlieren. Das Ergebnis hiervon wäre
das Ereignis, den 1. Wurf zu gewinnen und zu verlieren. Das Ergebnis hiervon wäre 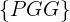 .
. 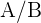 ist das Ereignis, zu gewinnen, wenn der 1. Wurf bereits verloren wurde.
ist das Ereignis, zu gewinnen, wenn der 1. Wurf bereits verloren wurde.
Ausgehend von den oben genannten Ergebnissen gilt 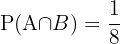 ,
, 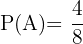 . Und somit:
. Und somit:
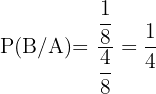
Die Gewinnwahrscheinlichkeit ist also  .
.
Unabhängige Ereignisse
Sie beeinflussen sich gegenseitig nicht.
Beispiel:
Zwei Personen werfen einen Gegenstand auf dasselbe Ziel, aber die erste Person, die wir  nennen, hat eine Wahrscheinlichkeit von
nennen, hat eine Wahrscheinlichkeit von  , das Ziel zu treffen, und die zweite Person, die wir
, das Ziel zu treffen, und die zweite Person, die wir  nennen, hat eine Wahrscheinlichkeit von
nennen, hat eine Wahrscheinlichkeit von  , das Ziel zu treffen. Wie groß ist die Wahrscheinlichkeit, dass die beiden Personen das Ziel treffen?
, das Ziel zu treffen. Wie groß ist die Wahrscheinlichkeit, dass die beiden Personen das Ziel treffen?
Wir haben also 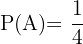 ,
, 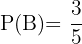 und müssen
und müssen  mit der folgenden Formel berechnen:
mit der folgenden Formel berechnen:
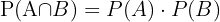
Das Ergebnis wäre 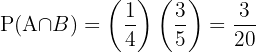
Abhängige Ereignisse
Sie beeinflussen sich gegenseitig.
Beispiel:
In einer Bevölkerung leiden  % der Menschen an einer Krankheit. Es gibt ein Verfahren zur Diagnose, das jedoch nicht völlig zuverlässig ist, da es in
% der Menschen an einer Krankheit. Es gibt ein Verfahren zur Diagnose, das jedoch nicht völlig zuverlässig ist, da es in  % der Fälle positiv ausfällt. Wie hoch ist die Wahrscheinlichkeit, die Krankheit zu haben und positiv zu testen?
% der Fälle positiv ausfällt. Wie hoch ist die Wahrscheinlichkeit, die Krankheit zu haben und positiv zu testen?
Wir nennen  das Ereignis, positiv auf die Krankheit zu testen und
das Ereignis, positiv auf die Krankheit zu testen und  das Ereignis des Auftretens der Krankheit. Wir haben somit
das Ereignis des Auftretens der Krankheit. Wir haben somit 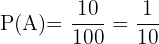 ,
, 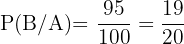 und berechnen
und berechnen 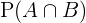 mit der Formel:
mit der Formel:
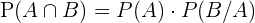
Somit:
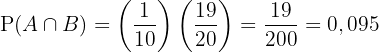
Das Ergebnis ist eine Wahrscheinlichkeit von 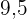 %.
%.
Differenz von Ereignissen
Sie können miteinander zusammenhängen oder auch nicht, und wir wollen, dass die Wahrscheinlichkeit des einen nichts mit der des anderen zu tun hat.
Beispiel:
Ein Würfel wird geworfen und wir wollen die Wahrscheinlichkeit berechnen, dass eine gerade Zahl herauskommt, aber kein Vielfaches von  . Wir nennen
. Wir nennen  also das Ereignis, dass eine gerade Zahl gewürfelt wird,
also das Ereignis, dass eine gerade Zahl gewürfelt wird,  das Ereignis, dass ein Vielfaches von
das Ereignis, dass ein Vielfaches von  gewürfelt wird. Wir haben
gewürfelt wird. Wir haben 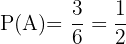 ,
, 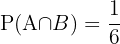 . Da
. Da 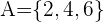 ,
, 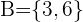 ,
, 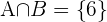 , verwenden wir die Formel:
, verwenden wir die Formel:
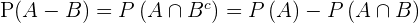
Somit:
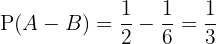
Gesetz der totalen Wahrscheinlichkeit
Dies ist der Fall, wenn mehrere unabhängige oder nicht miteinander zusammenhängende Ereignisse vorliegen, die jedoch alle mit einem anderen Ereignis zusammenhängen, dessen Wahrscheinlichkeit du erfahren möchtest.
Wenn wir ein Ereignis  haben und
haben und 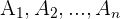 sich gegenseitig ausschließende Ereignisse sind, wenden wir folgende Formel an:
sich gegenseitig ausschließende Ereignisse sind, wenden wir folgende Formel an:
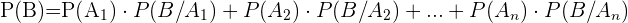
Beispiel:
Eine Fabrik nutzt drei Maschinen 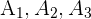 für die Herstellung von bestimmten Produkten. Wir nehmen Folgendes an:
für die Herstellung von bestimmten Produkten. Wir nehmen Folgendes an:
Maschine 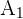 produziert 55% aller Produkte, von denen 2% fehlerhaft sind.
produziert 55% aller Produkte, von denen 2% fehlerhaft sind.
Maschine 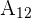 produziert 25% aller Produkte, von denen 4% fehlerhaft sind.
produziert 25% aller Produkte, von denen 4% fehlerhaft sind.
Maschine 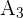 produziert 20% aller Produkte, von denen 5% fehlerhaft sind.
produziert 20% aller Produkte, von denen 5% fehlerhaft sind.
Wie groß ist die Wahrscheinlichkeit, dass ein ausgewählter Artikel fehlerhaft ist?
 ist das Ereignis, dass der Artikel fehlerhaft ist. Somit:
ist das Ereignis, dass der Artikel fehlerhaft ist. Somit:
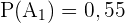 ,
, 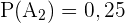 ,
, 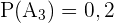 ,
, 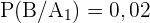 ,
, 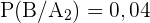 und
und 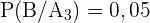
Wir wenden die Formel an:
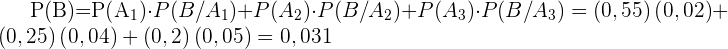
Die Wahrscheinlichkeit ist also 3,1%.
Satz von Bayes
Dieser Satz erleichtert Übungen zur bedingten Wahrscheinlichkeit bei mehreren Ereignissen.
Wenn wir ein Ereignis  haben und
haben und 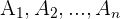 sich gegenseitig ausschließende Ereignisse sind, verwenden wir folgende Formel:
sich gegenseitig ausschließende Ereignisse sind, verwenden wir folgende Formel:
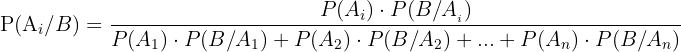
In einer Fabrik arbeiten drei Mitarbeiter: Andreas, Beto und Carlos. Andrés ist zu 50%, Beto zu 30% und Carlos zu 20% an der Produktion beteiligt.Bei Andreas liegt die Wahrscheinlichkeit bei 1%, dass er etwas falsch macht; bei Beto liegt die Wahrscheinlichkeit bei 2% und bei Carlos liegt sie bei 3%. Eines der Produkte wurde getestet und war fehlerhaft. Wie hoch ist die Wahrscheinlichkeit, dass es Andreas war, der den Fehler gemacht hat?
Wir beachten das Folgende:
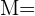 {fehlerhafte Arbeit},
{fehlerhafte Arbeit}, 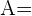 {von Andreas ausgeführt},
{von Andreas ausgeführt}, 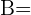 {von Beto ausgeführt} und
{von Beto ausgeführt} und 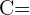 {von Carlos ausgeführt}.
{von Carlos ausgeführt}.
Anhand dieser Ereignisse erhalten wir folgende Wahrscheinlichkeiten:
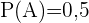 ,
, 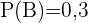 ,
, 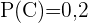 ,
, 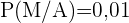 ,
, 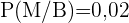 und
und 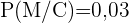 .
.
Wir wenden den Satz von Bayes an, um die Wahrscheinlichkeit zu ermitteln, dass Andreas den Fehler gemacht hat
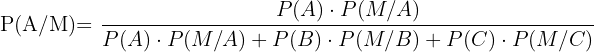
Wir setzen die Werte ein und erhalten
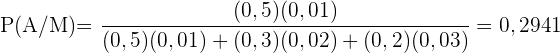
Gesetze
1 Gesetz, das besagt, dass die Wahrscheinlichkeit nicht-negativ und kleiner als 1 ist. Dieses Gesetz besagt, dass die Wahrscheinlichkeit in Prozenten von  % bis
% bis  % angegeben wird, weshalb
% angegeben wird, weshalb  % bedeutet, dass es keine Wahrscheinlichkeit gibt,
% bedeutet, dass es keine Wahrscheinlichkeit gibt,  %, dass die Vorhersage eintritt. Die Werte dazwischen geben an, wie wahrscheinlich es ist, dass das erwartete Ereignis eintritt.
%, dass die Vorhersage eintritt. Die Werte dazwischen geben an, wie wahrscheinlich es ist, dass das erwartete Ereignis eintritt.
Gesetze
1 Gesetz, das besagt, dass die Wahrscheinlichkeit nicht-negativ und kleiner als 1 ist. Dieses Gesetz besagt, dass die Wahrscheinlichkeit in Prozenten von  % bis
% bis  % angegeben wird, weshalb
% angegeben wird, weshalb  % bedeutet, dass es keine Wahrscheinlichkeit gibt,
% bedeutet, dass es keine Wahrscheinlichkeit gibt,  %, dass die Vorhersage eintritt. Die Werte dazwischen geben an, wie wahrscheinlich es ist, dass das erwartete Ereignis eintritt.
%, dass die Vorhersage eintritt. Die Werte dazwischen geben an, wie wahrscheinlich es ist, dass das erwartete Ereignis eintritt.
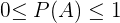
2 Gesetz, dass ein Ereignis mit Sicherheit eintritt. Ein Beispiel für dieses Gesetz wäre ein Würfel, in den auf allen Seiten die Zahl  eingraviert ist. Die Wahrscheinlichkeit, dass beim Würfeln
eingraviert ist. Die Wahrscheinlichkeit, dass beim Würfeln  herauskommt, beträgt dann
herauskommt, beträgt dann  %.
%.
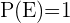
3 Gesetz, dass ein Ereignis sicher nicht eintritt. Für dieses Gesetz nehmen wir den gleichen Würfel wie im vorherigen Beispiel und würfeln. Wie groß wäre die Wahrscheinlichkeit, dass eine  gewürfelt wird? Die Wahrscheinlichkeit wäre gleich 0, weil es nur die Zahl
gewürfelt wird? Die Wahrscheinlichkeit wäre gleich 0, weil es nur die Zahl  gibt und die Wahrscheinlichkeit daher
gibt und die Wahrscheinlichkeit daher  ist.
ist.
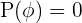
4 Gegenereignis. Für dieses Gesetz nehmen wir an, wir werfen einen normalen Würfel mit den Zahlen  bis
bis  und wollen die Wahrscheinlichkeit ermitteln, dass
und wollen die Wahrscheinlichkeit ermitteln, dass  nicht erscheint. Wir nennen also
nicht erscheint. Wir nennen also  das Ereignis, dass
das Ereignis, dass  gewürfelt wird,
gewürfelt wird, 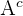 wäre das Ereignis, dass
wäre das Ereignis, dass  nicht gewürfelt wird und
nicht gewürfelt wird und 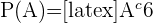 . Wir wenden also die Formel an:
. Wir wenden also die Formel an:
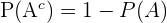
Wir setzen ein:
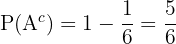 .
.
Mit KI zusammenfassen:












