Kapitel
Fakultät einer Zahl
Die Fakultät einer positiven ganzen Zahl 
ist das Produkt aller positiver ganzer Zahlen von 
bis . Mit anderen Worten: Man muss alle natürlichen Zahlen zwischen dieser Zahl und multiplizieren.
Die Fakultät wird durch ein Ausrufezeichen „!“ nach einer Zahl dargestellt und die Fakultät von ist dann
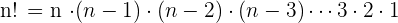
Die Fakultät von 5 ist zum Beispiel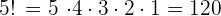 
Variationen
Die Variation ist jedes der möglichen Tupel, die aus einer Gruppe von Elementen gebildet werden können.
Wenn wir 
Elemente haben, können wir Tupel mit Elementen bilden, die eine Vielzahl von Alternativen bieten. Dies hängt davon ab, ob es möglich ist, Elemente im selben Tupel zu wiederholen oder nicht.
Wenn keine sich wiederholenden Elemente erlaubt sind, wird die Anzahl der n-Tupel, in denen sich keines der Elemente wiederholt, als Anzahl der sich nicht wiederholenden Variationen bezeichnet und durch folgende Formel ermittelt
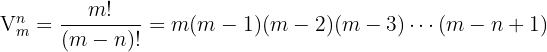
Wenn in jedem Tupel ein Element mehr als einmal wiederholt werden kann, spricht man von der Anzahl der Variationen mit Wiederholung:
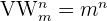
Permutationen
Eine Permutation ist die mögliche Anordnung der Elemente, die Teil einer Menge sind. Das heißt, es handelt sich um eine Änderung der Art und Weise, wie die Elemente angeordnet sind.
Die Anzahl der Permutationen in einer Menge von Elementen ist
Es gibt zum Beispiel sechs Permutationen der Menge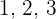 
. Sie hat somit 
Elemente und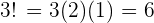 
. Diese sind
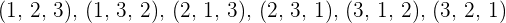
Kreisförmige Permutationen
Kreisförmige Permutationen sind ein Sonderfall der Permutationen.
Sie werden verwendet, wenn die Elemente „im Kreis“ angeordnet werden sollen (z. B. die Gäste an einem Tisch), so dass das erste Element, das in die Stichprobe „eingefügt“ wird, den Anfang und das Ende der Stichprobe bestimmt.
Die Anzahl der Permutationen von Elementen ist in diesem Fall
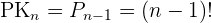
Permutationen mit Wiederholung
Eine Permutation mit Wiederholung besteht aus einer Permutation von m Elementen, von denen es mehrere gibt, die einander gleich sind.
Angenommen, in der Menge von sind nicht alle Elemente unterschiedlich, sondern das erste Element wiederholt sich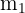 
Male, das zweite wiederholt sich 
Male, ..., das n-te wiederholt sich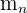 
Male. Daraus folgt, dass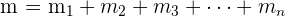
Die Anzahl der Permutationen der sich wiederholenden Elemente beträgt dann:
Permutationen des ersten Elements: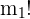 
Permutationen des zweiten Elements: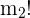 
Permutationen des n-ten Elements: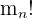 
Diese Permutationen identischer Elemente sind untereinander gleich. Die verschiedenen Möglichkeiten, die -Elemente anzuordnen, wären also
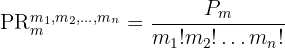
Kombinationen
Kombinationen von Elementen aus in mit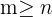 
sind alle möglichen Gruppierungen, die mit den -Elementen so gebildet werden können, dass:
Nicht alle Elemente passen.
Die Reihenfolge spielt keine Rolle.
Keine Wiederholung von Elementen.
Diese werden wie folgt berechnet:
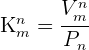
Wir können die Kombinationen auch anhand von Faktultäten berechnen:
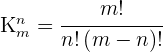
Kombinationen mit Wiederholung
Kombinationen mit sich wiederholenden Elementen aus in mit 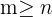sind die verschiedenen Gruppen, die von Elementen so gebildet werden, dass:
Nicht alle Elemente passen.
Die Reihenfolge spielt keine Rolle.
Wiederholung von Elementen.
Die Anzahl der Kombinationen mit Wiederholungen wird mit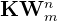 
bezeichnet. Das Problem besteht also darin, den Wert von 
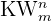zu bestimmen, den wir mit der folgenden Formel berechnen können:
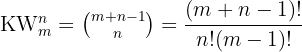
Kombinatorische Zahlen
Die kombinatorischen Zahlen werden wie folgt angegeben:
,
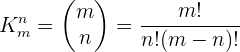wobei 
und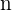 
ganze Zahlen sind und 
.
Eigenschaften von kombinatorischen Zahlen:
1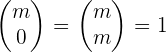 
2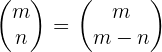 
3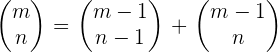 
Binomischer Lehrsatz
Der binomische Lehrsatz ist die Formel, mit der wir die Potenzen eines Binoms ermitteln können. Die Formel lautet
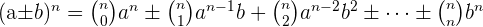
Term an k-ter Stelle
Die folgenden Formeln geben den Term an der Stelle 
in der Erweiterung des bionomischen Lehrsatzes an:
1 Der k-te Term des Binoms 
ist
2 Der k-te Term des Binoms 
ist
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
