Wenn man versucht, ein Gleichungssystem zu lösen, kann man feststellen, dass es viele verschiedene Möglichkeiten gibt, wie z. B. die das Gauß-Verfahren, die Cramersche Regel oder der Satz von Kronecker-Capelli.
Dies führt uns zu der Frage: Welche Methode ist die beste?
Im Folgenden werden wir diese Methoden anhand der Lösung verschiedener Gleichungssysteme vergleichen und die Vor- und Nachteile jeder der genannten Methoden diskutieren.
Homogene Systeme
Wenn alle unabhängigen Terme eines Systems mit 
Gleichungen und 
Variablen 0 sind, ist das System homogen.
Es gilt die triviale Lösung: 
Die notwendige und hinreichende Bedingung dafür, dass ein homogenes System andere Lösungen als die triviale hat, ist, dass der Rang der Koeffizientenmatrix kleiner ist als die Anzahl der Unbekannten, oder mit anderen Worten, dass die Determinante der Koeffizientenmatrix 0 ist.
Dies sagt uns nur, dass das System eine andere Lösung als die triviale hat, aber es sagt uns natürlich nicht, welche das ist. Um sie zu berechnen, können wir also die oben genannten Methoden anwenden.
Beispiel
Löse das folgende Gleichungssystem:
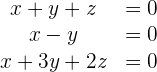
Lösung mit dem Gauß-Jordan-Algorithmus
1Bilde eine Matrix aus den Koeffizienten und den unabhängigen Termen.
Als Erstes müssen wir eine Matrix mit den Koeffizienten und den unabhängigen Termen (Zahlen auf der rechten Seite der Gleichheitszeichen der Gleichungen) der Gleichungen wie folgt bilden:
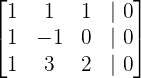
2Mit etwas Algebra kann man nun das Gaußsche Eliminationsverfahren durchführen.
Nun führen wir die entsprechenden Rechenoperationen durch, um die Lösung des Systems zu ermitteln:
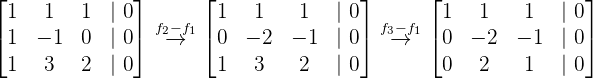
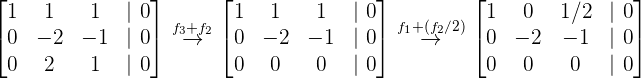
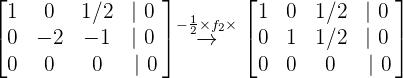
Daraus ergeben sich folgende Gleichungen:
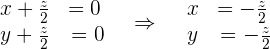
3Wir schreiben die Variablen um.
In diesem Fall nehmen wir 
und erhalten: 
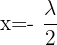und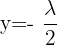 
.
Dies bedeutet, dass alle Variablen in Form einer einzigen Variablen vorliegen.
Dies bedeutet, dass das System unendlich viele Lösungen hat.
Lösung mit der Cramerschen Regel
1Bilde die Koeffizientenmatrix und berechne die Determinante.
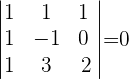
2Da die Determinante der Koeffizientenmatrix 
ist, können wir die Cramersche Regel nicht anwenden. Dies kann darauf hindeuten, dass das System keine Lösung oder unendlich viele Lösungen hat.
Lösung mit dem Satz von Kronecker-Capelli.
1Wir bilden die Koeffizientenmatrix.
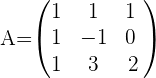
2Wir berechnen den Rang der Koeffizientenmatrix.
In diesem Fall ist der Rang der Matrix:
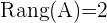
3Wir bilden die erweiterte Matrix.
Nun fügen wir die unabhängigen Terme des Gleichungssystems (Zahlen auf der rechten Seite des Gleichheitszeichens der Gleichungen) zur Matrix hinzu und bilden so die erweiterte Matrix:
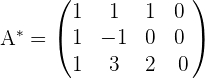
4Wir berechnen den Rang der erweiterten Matrix.
In diesem Fall ist der Rang der erweiterten Matrix:
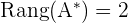
5Wir wenden den Satz von Kronecker-Capelli an.
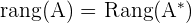Lösbares System. 
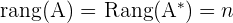Eindeutig lösbares System.
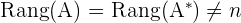Nicht eindeutig lösbares System.
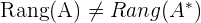Keine Lösung.
ist hierbei die Anzahl der Variablen.
Da die Ränge der beiden Matrizen übereinstimmen, ist das System lösbar, und da der Rang kleiner ist als die Anzahl der Unbekannten, ist das System jedoch nicht eindeutig lösbar. Das bedeutet, dass das System unendlich viele Lösungen hat.
Inhomogene Systeme
Ein Gleichungssystem wird als inhomogen bezeichnet, wenn jede der am System beteiligten Gleichungen gleich einer Zahl ungleich null ist.
Beispiel
Löse das folgende Gleichungssystem:
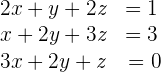
Lösung mit dem Gauß-Jordan-Algorithmus
1Wir bilden die Matrix mit den Koeffizienten und den unabhängigen Termen
Als Erstes müssen wir eine Matrix mit den Koeffizienten und den unabhängigen Termen (Zahlen auf der rechten Seite der Gleichheitszeichen der Gleichungen) der Gleichungen wie folgt bilden:
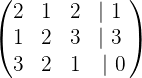
2Mit etwas Algebra kann man nun das Gaußsche Eliminationsverfahren durchführen.
Bevor wir mit der Durchführung der Berechnungen beginnen, ändern wir die Position der Zeilen der Matrix auf folgende Weise, um die Auflösung zu erleichtern.
x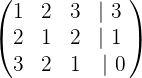
Wir führen nun die entsprechenden Rechenoperationen durch, um die Lösung des Systems zu ermitteln:
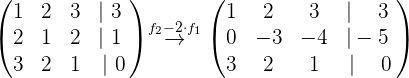
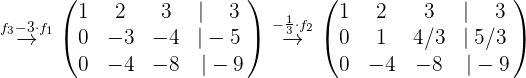
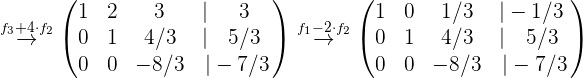
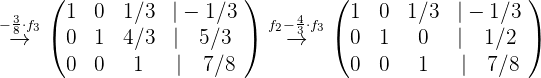
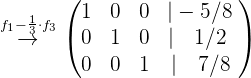
Die Lösung des Systems ist:
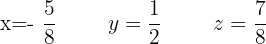
Lösung mit der Cramerschen Regel
1Bilde die Koeffizientenmatrix und berechne die Determinante.
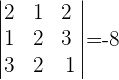
2Da die Determinante ungleich 0 ist, ist die Matrix regelmäßig und das System hat nur eine Lösung (eindeutig lösbares System).
3Wir fahren mit dem Vorgang fort, um das System zu lösen.
Nun ersetzen wir die erste Spalte der Koeffizientenmatrix durch eine Spalte, die aus den unabhängigen Termen (Zahlen auf der rechten Seite der Gleichheitszeichen der Gleichungen) gebildet wird, und berechnen die Determinante.
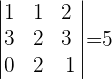
Nun ist der Wert der Variable 
gegeben durch:
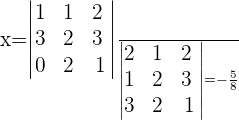
Wenn wir ähnlich vorgehen, können wir den Wert der verbleibenden Variablen ermitteln, indem wir die zweite Spalte der Koeffizientenmatrix durch die Spalte der unabhängigen Terme ersetzen. Indem wir die Determinante berechnen, ermitteln wir den Wert von 
auf ähnliche Weise wie . Dasselbe gilt für die Variable 
, wobei wir die dritte Spalte ändern. Wir berechnen und erhalten:
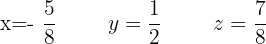
Lösung mit dem Satz von Kronecker-Capelli
1Wir bilden die Koeffizientenmatrix
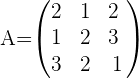
2Wir berechnen den Rang der Koeffizientenmatrix.
In diesem Fall ist der Rang der Matrix:
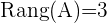
3Wir bilden die erweiterte Matrix.
Nun fügen wir die unabhängigen Terme des Gleichungssystems (Zahlen auf der rechten Seite des Gleichheitszeichens der Gleichungen) zur Matrix hinzu und bilden so die erweiterte Matrix:
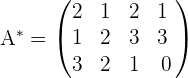
4Berechne den Rang der erweiterten Matrix.
In diesem Fall ist der Rang der erweiterten Matrix:
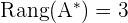
5Wir wenden den Satz von Kronecker-Capelli an.
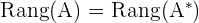Lösbares System. 
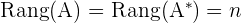Eindeutig lösbares System.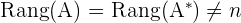- Nicht eindeutig lösbares System.
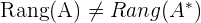- Keine Lösung.
ist hierbei die Anzahl der Variablen.
Da die Ränge der beiden Matrizen übereinstimmen, ist das System lösbar, und da der Rang gleich der Anzahl der Unbekannten ist, ist das System eindeutig lösbar. Dies bedeutet, dass es nur eine einzige Lösung gibt.
Gleichungssystem mit Parametern
In diesem Abschnitt wollen wir uns ansehen, wie man Gleichungssysteme mit Parametern mit den bisher vorgestellten Methoden lösen kann.
Beispiel
Löse das folgende Gleichungssystem:
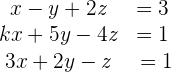
Lösung mit dem Gauß-Jordan-Algorithmus
1Bilde eine Matrix aus den Koeffizienten und den unabhängigen Termen.
Als Erstes müssen wir eine Matrix mit den Koeffizienten und den unabhängigen Termen (Zahlen auf der rechten Seite der Gleichheitszeichen der Gleichungen) der Gleichungen wie folgt bilden:
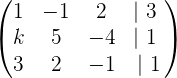
2Mit etwas Algebra kann man nun das Gaußsche Eliminationsverfahren durchführen.
Nun führen wir die entsprechenden Rechenoperationen durch, um die Lösung des Systems zu ermitteln
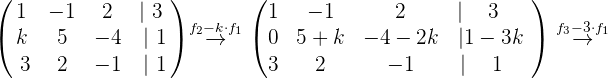
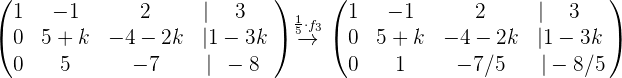
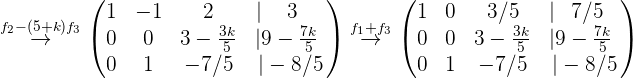
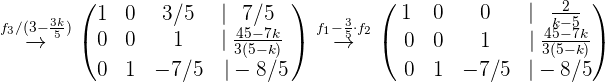
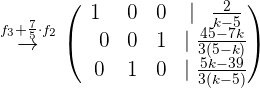
Wir stellen schnell fest, dass das Gleichungssystem nicht gelöst werden kann, wenn 
ist. Deshalb nehmen wir an, dass 
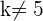ist.
Somit ist die Lösung des Systems:
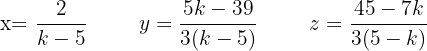
Lösung mit der Cramerschen Regel
1Bilde die Koeffizientenmatrix und berechne die Determinante.
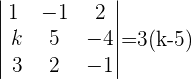
2Wenn ist, ist die Determinante . Das würde bedeuten, dass wir die Cramersche Regel nicht anwenden können. Daher gehen wir davon aus, dass 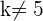ist.
3Wir ersetzen die erste Spalte durch die Spalte der unabhängigen Terme und berechnen die Determinante.
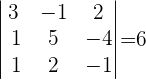
4Wir ersetzen die zweite Spalte durch die Spalte der unabhängigen Terme und berechnen die Determinante.
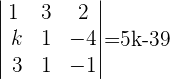
5Wir ersetzen die dritte Spalte durch die Spalte der unabhängigen Terme und berechnen die Determinante.
5Wir berechnen den Wert der Variablen , und .
Aus der Cramerschen Regel geht hervor:
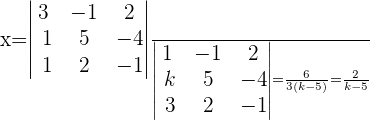
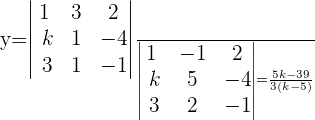
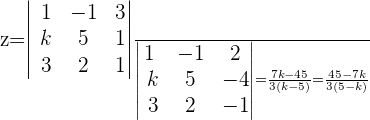
Lösung mit dem Satz von Kronecker-Capelli
1Bilde die Koeffizientenmatrix.
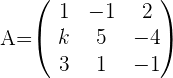
2Berechne den Rang der Koeffizientenmatrix.
In diesem Fall hängt der Rang der Matrix von der Determinante der Matrix ab, die lautet:
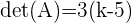
Wenn ist, ist somit die Determinante 
. Somit ist der Rang der Matrix .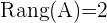
Wenn nun 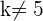ist, ist somit die Determinante 
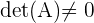. In diesem Fall ist der Rang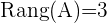
3Bilde die erweiterte Matrix.
Nun fügen wir die unabhängigen Terme des Gleichungssystems (Zahlen auf der rechten Seite des Gleichheitszeichens der Gleichungen) zur Matrix hinzu und bilden so die erweiterte Matrix:
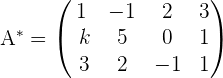
4Berechne den Rang der erweiterten Matrix.
In diesem Fall ist der Rang der erweiterten Matrix:
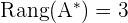
5Wir wenden den Satz von Kronecker-Capelli an.
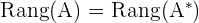- Lösbares System.
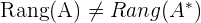- Keine Lösung.
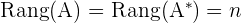- Eindeutig lösbares System.
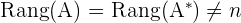- Nicht eindeutig lösbares System.
ist hierbei die Anzahl der Variablen.
Wenn ist, ist der Rang der Matrizen unterschiedlich und es handelt sich daher um ein nicht lösbares Gleichungssystem.
Wenn 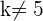ist, stimmen die Ränge der beiden Matrizen überein und das System ist somit lösbar. Und da außerdem der Rang gleich der Anzahl der Unbekannten ist, ist das System eindeutig lösbar, was bedeutet, dass es nur eine Lösung hat.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 15) | 12,5 | 3 | 37,5 |
| [15, 20) | 17,5 | 5 | 87,5 |
| [20, 25) | 22,5 | 7 | 157,5 |
| [25, 30) | 27,5 | 4 | 110 |
| [30, 35) | 32,5 | 2 | 65 |
| 21 | 457,5 |
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
