Beantworte die folgenden Fragen und runde gegebenenfalls auf zwei Dezimalstellen:
1 Berechne die Wahrscheinlichkeit, dass beim Würfeln folgende Augenzahl fällt:
Eine ungerade Zahl
Dieses Feld ist erforderlich.
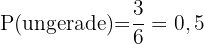
Ein Vielfaches von 
Dieses Feld ist erforderlich.
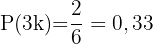
Eine Zahl kleiner als 
Dieses Feld ist erforderlich.
{P(<5)=\displaystyle\frac{4}{6}=0,67}[/latex]
2 In einer Urne befinden sich 
weiße Kugeln, schwarze und 
rote Kugeln. Wenn eine Kugel zufällig gezogen wird, berechne die Wahrscheinlichkeit, dass:
Die Kugel weiß ist.
Dieses Feld ist erforderlich.
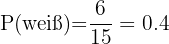
Die Kugel schwarz ist
Dieses Feld ist erforderlich.
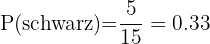
Die Kugel nicht rot ist.
Dieses Feld ist erforderlich.
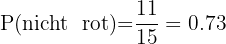
3 Aus einer Urne, die weiße und schwarze Kugeln enthält, werden 
Kugeln nach dem Zufallsprinzip mit Zurücklegen entnommen. Berechne die Wahrscheinlichkeit, dass:
Beide Kugeln schwarz sind.
Dieses Feld ist erforderlich.
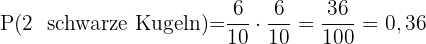
Eine Kugel ist weiß, die andere ist schwarz.
Dieses Feld ist erforderlich.
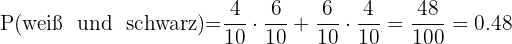
4 Aus einer Urne, die weiße und schwarze Kugeln enthält, werden zwei Kugeln nach dem Zufallsprinzip ohne Zurücklegen entnommen. Berechne die Wahrscheinlichkeit, dass:
Die beiden Kugeln sind schwarz
Dieses Feld ist erforderlich.
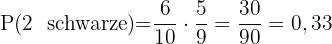
Eine Kugel ist weiß, die andere Kugel ist schwarz.
Dieses Feld ist erforderlich.
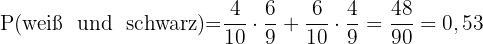
5 Zwei Würfel werden geworfen und die Summe der erzielten Punkte wird notiert. Berechne:
Die Wahrscheinlichkeit, dass die Summe ist.
Dieses Feld ist erforderlich.
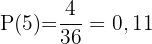
Die Wahrscheinlichkeit, dass die Summe 
ist.
Dieses Feld ist erforderlich.
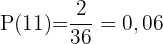
6Aus einem Kartenspiel mit 
Karten werden gleichzeitig Karten gezogen. Berechne die Wahrscheinlichkeit, dass:
Beide Karten zeigen Pik.
Dieses Feld ist erforderlich.
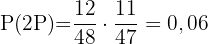
Mindestens einmal Pik.
Dieses Feld ist erforderlich.
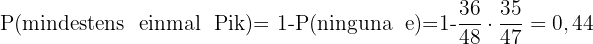
Einmal Pik und einmal Herz.
Dieses Feld ist erforderlich.
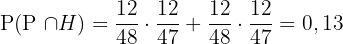
7Johannes und Peter gehen auf die Jagd, wobei wir wissen, dass Johannes 
von Schüssen trifft und Peter von Schüssen. Berechne die Wahrscheinlichkeit, dass:
Johannes trifft ein Tier.
Dieses Feld ist erforderlich.
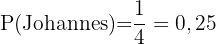
Peter trifft ein Tier.
Dieses Feld ist erforderlich.
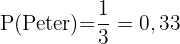
Beide treffen dasselbe Tier.
Dieses Feld ist erforderlich.
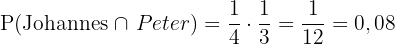
Mindestens einer von beiden trifft das Tier.
Dieses Feld ist erforderlich.
Die Wahrscheinlichkeit ist, dass entweder Johannes oder Peter trifft, abzüglich der Wahrscheinlichkeit, dass beide gleichzeitig treffen.
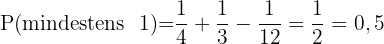
8 In einer Klasse gibt es 
Schülerinnen mit Brille und 
ohne Brille, Schüler mit Brille und Schüler ohne Brille. An einem Tag sind 
Schüler*innen anwesend. Berechne die Wahrscheinlichkeit, dass der/die fehlende Schüler*in:
männlich
Dieses Feld ist erforderlich.
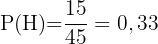
weiblich ohne Brille
Dieses Feld ist erforderlich.
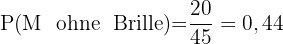
männlich oder weiblich
Dieses Feld ist erforderlich.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
