
Was sind Kontingenztabellen
Eine nützliche Methode zur Klassifizierung der bei einer Zählung gewonnenen Daten sind Kontingenztabellen.
In der Statistik werden sie zur Erfassung und Analyse des Zusammenhangs zwischen zwei oder mehr Variablen verwendet, die in der Regel qualitativer Natur sind (nominal oder ordinal).
Es handelt sich um Tabellen, deren Zellen Wahrscheinlichkeiten enthalten, und in denen wir einige Wahrscheinlichkeiten durch die Kenntnis anderer Wahrscheinlichkeiten in der Tabelle bestimmen können.
Beispiel zur Lösung eines Problems mit einer Kontingenztabelle
Unter den  besten Kunden eines Autohauses wird eine Reise nach Rom verlost. Davon sind
besten Kunden eines Autohauses wird eine Reise nach Rom verlost. Davon sind  Frauen,
Frauen,  Personen sind verheiratet und
Personen sind verheiratet und  sind verheiratete Frauen.
sind verheiratete Frauen.
- Wie hoch ist die Wahrscheinlichkeit, dass ein nicht verheirateter Mann die Reise gewinnt?
- Wenn der oder die Gewinner*in bekanntlich verheiratet ist, wie groß ist dann die Wahrscheinlichkeit, dass es sich um eine Frau handelt?
Lösung
Es gibt zwei Variablen, die erste ist das Geschlecht (Männer - Frauen) und die zweite ist der Familienstand, in diesem Fall, ob die Person ledig oder verheiratet ist.
Die Aufgabe fragt uns nach der Wahrscheinlichkeit, dass der oder die Gewinner*in ein lediger Mann ist. Zunächst wissen wir nicht, wie viele ledige Männer es gibt, denn wir haben diese Daten nicht. Also hilft es uns, eine Kontingenztabelle zu erstellen.
1 Wir erstellen eine entsprechende Tabelle mit den gegebenen Daten
Anhand der expliziten Daten, die wir haben, sieht unsere Tabelle wie folgt aus:
| Männer | Frauen | Gesamt | |
|---|---|---|---|
| verheiratet | 45 | 80 | |
| ledig | |||
| gesamt | 65 | 120 |
2 Wir analysieren die Daten
Hier besteht der nächste Schritt darin, die vorhandenen Daten zu nutzen, um den Rest zu erhalten. Dieser Vorgang kann auf verschiedene Weise durchgeführt werden.
Wir wissen, dass  Kund*innen verheiratet sind und von diesen sind
Kund*innen verheiratet sind und von diesen sind  Frauen. Deshalb müssen
Frauen. Deshalb müssen  Personen männlich sein.
Personen männlich sein.
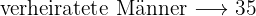
Wenn es  Frauen gibt und
Frauen gibt und  davon verheiratet sind, müssen
davon verheiratet sind, müssen  ledig sein.
ledig sein.
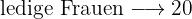
Von den  Kund*innen sind
Kund*innen sind  verheiratet. Deshalb müssen
verheiratet. Deshalb müssen  davon ledig sein.
davon ledig sein.
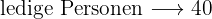
Außerdem sind von den  Kund*innen
Kund*innen  Frauen. Somit sind
Frauen. Somit sind  davon Männer.
davon Männer.
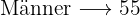
Es gibt  ledige Personen, von denen
ledige Personen, von denen  Frauen sind. Somit sind die verbleibenden
Frauen sind. Somit sind die verbleibenden  Personen Männer
Personen Männer
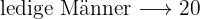
3 Wir vervollständigen die Tabelle
| Männer | Frauen | Gesamt | |
|---|---|---|---|
| verheiratet | 35 | 45 | 80 |
| ledig | 20 | 20 | 40 |
| gesamt | 55 | 65 | 120 |
4 Wir ermitteln die Wahrscheinlichkeiten
Um nun die Fragen beanworten zu können, müssen wir den Satz von Moivre-Laplace anwenden. Das heißt:
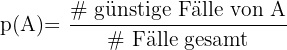
Wie hoch ist die Wahrscheinlichkeit, dass ein lediger Mann die Reise gewinnt?
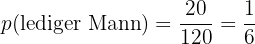
Wenn der oder die Gewinnerin bekanntlich verheiratet ist, wie groß ist dann die Wahrscheinlichkeit, dass es sich um eine Frau handelt?
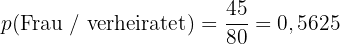
Mit KI zusammenfassen:












