Definition von Permutationen
Unter einer Permutation versteht man das Anordnen von Elementen an verschiedenen Stellen.
Permutationen von 
Elementen in 
Positionen sind die verschiedenen Möglichkeiten, wie die Elemente geordnet werden können, indem nur die Positionen besetzt werden. Vorausgesetzt, dass 
.
Dabei muss Folgendes beachtet werden:
- Die Reihenfolge spielt eine Rolle, da der Austausch zwischen zwei verschiedenen Elementen eine neue Permutation ergibt.
- Die Elemente werden nicht wiederholt, denn wenn sie sich wiederholen oder gleich sind, führt ihr Austausch nicht zu einer neuen Permutation.
Die folgende Formel wird verwendet, um die Gesamtzahl der Möglichkeiten zu ermitteln mit denen die m Elemente in n Positionen platziert werden können:
Wenn in einem gegebenen Fall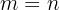 
ist, wird die folgende Formel verwendet, um die Gesamtzahl der Permutationen zu berechnen:
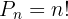
Analysiere nun die folgenden Beispiele anhand der oben genannten Angaben.
Beispiele für Problemstellungen bei Permutationen
1 Berechne die Permutationen von 
Elementen in Positionen.
Lösung:
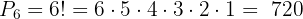
2 Wie viele Zahlen mit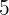 
verschiedenen Ziffern lassen sich mit den Ziffern: 
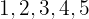bilden?
Lösung:
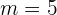und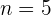 
- Alle Elemente passen, da wir dieselbe Anzahl von Elementen wie Positionen haben
- Die Reihenfolge spielt eine Rolle
- Die Elemente werden nicht wiederholt. Laut Erläuterung müssen die Zahlen unterschiedlich sein
3 Auf wie viele verschiedene Arten können acht Personen in einer Reihe mit acht Sitzen sitzen?
Lösung:
- Alle Elemente passen. Alle
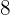Personen müssen sich hinsetzen können - Die Reihenfolge spielt eine Rolle
- Die Elemente werden nicht wiederholt. Eine Person kommt nicht mehrmals vor
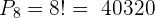
4 Wie viele Möglichkeiten gibt es, die Buchstaben 
an drei Stellen zu platzieren?
Lösung:
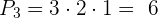
Hier werden die Formen bei der Berechnung herangezogen:
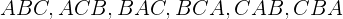
5 Wir haben 
Elemente und möchten diese auf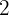 
Positionen verteilen. Auf wie viele Arten können wir das tun?
Lösung:
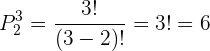
Drei Elemente 
auf zwei Positionen:
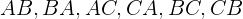
Es gibt viele Anwendungen von Permutationen, weil es sehr komplexe Zählungen gibt, die auf diese Weise vereinfacht werden können. Bei Permutationen muss darauf geachtet werden, dass es auf die Reihenfolge ankommt, in der die Elemente angeordnet sind.
Wendest du im Alltag auch manchmal Permutationen an?
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
