Willkommen auf unserer Seite, auf der wir uns mit Aufgaben zur Regression und Korrelation beschäftigen! Regression und Korrelation sind grundlegende Instrumente der Datenanalyse, die in einer Vielzahl von Bereichen eingesetzt werden, von der wissenschaftlichen Forschung bis hin zur Entscheidungsfindung in Unternehmen.
In diesem Artikel findest du eine Reihe von praktischen Übungen, die dir helfen sollen, die wichtigsten Konzepte im Zusammenhang mit Regression und Korrelation zu verstehen und anzuwenden. Wir haben für dich klare und anspruchsvolle Beispiele zusammengestellt, in denen du die Gleichung der Regressionsgeraden finden, den linearen Korrelationskoeffizienten berechnen, die Varianz und die Kovarianz berechnen musst und vieles mehr.
Komm mit uns auf diese lehrreiche Reise, auf der wir die Statistik entmystifizieren und dich mit den Fähigkeiten ausstatten, die du brauchst, um Daten zu interpretieren, sinnvolle Beziehungen zu erkennen und fundierte Entscheidungen zu treffen. Beginnen wir mit der Erforschung der Verbindung zwischen Variablen und meistern wir Aufgaben zu Regression und Korrelation!
Die Kovarianz wird mit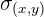 
dargestellt und ist durch folgende Ausdrücke gegeben
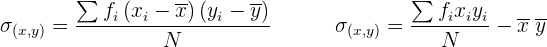
Die Gleichung der Regressionsgeraden bestimmen
Fünf Kinder im Alter von 2, 3, 5, 7 und 8 Jahren wiegen 14, 20, 32, 42 bzw. 44 kg.
1 Ermittle die Gleichung der Regressionsgeraden zwischen Alter und Gewicht.
2 Was wäre das ungefähre Gewicht eines sechsjährigen Kindes?
Fünf Kinder im Alter von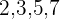 
und 
Jahren wiegen jeweils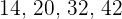 
und 
Kilo.
1 Ermittle die Gleichung der Regressionsgeraden zwischen Alter und Gewicht.
2 Was wäre das ungefähre Gewicht eines sechsjährigen Kindes?
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
| |  |  |  |
|  |  |  |  |
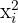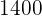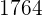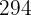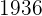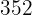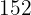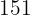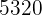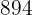Wir berechnen die Durchschnittswerte
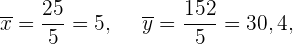
Wir berechnen die Kovarianz und die Varianz 
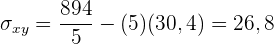
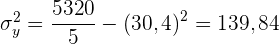
Die Regressionsgerade von Alter und Gewicht verläuft durch den Punkt 
und hat die Steigung 
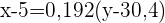
Wir berechnen und erhalten die Regressionsgerade
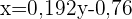
Um das ungefähre Gewicht eines sechsjährigen Kindes zu ermitteln, setzen wir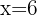 
in die Regressionsgleichung ein und erhalten
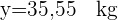
Berechnung des linearen Korrelationskoeffizienten
Ein Einkaufszentrum weiß, dass je nach Entfernung (in Kilometern) von einem Ballungszentrum einer Stadt die in der Tabelle angegebene Anzahl von Kunden (in Hunderten) dort einkauft:
Anzahl der Kunden  | Entfernung  |
|---|---|
|  |
|  |
 | |
|  |
|  |
 |  |
1 Berechne den linearen Korrelationskoeffizienten.
2 Wenn das Einkaufszentrum km entfernt ist, wie viele Kunden können dann erwartet werden?
3 Wenn Kunden dort einkaufen sollen, wie weit sollte es dann vom Ballungszentrum entfernt sein?
Ein Einkaufszentrum weiß, dass je nach Entfernung (in Kilometern) von einem Ballungszentrum einer Stadt die in der Tabelle angegebene Anzahl von Kunden (in Hunderten) dort einkauft:
| Anzahl der Kunden | Entfernung |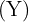
|---|---|
| |
| |
| |
| |
| |
| |
1 Berechne den linearen Korrelationskoeffizienten.
2 Wenn das Einkaufszentrum km entfernt ist, wie viele Kunden können dann erwartet werden?
3 Wenn Kunden dort einkaufen sollen, wie weit sollte es dann vom Ballungszentrum entfernt sein?
| | | | |
|---|---|---|---|---|
| |  | |  |
| |  | |  |
| |  |  |  |
| |  |  |  |
| |  | |  |
| | | |  |
|  |  |  |  |
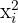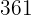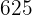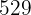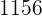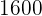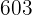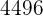Wir berechnen die Durchschnittswerte
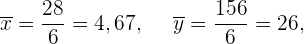
Wir berechnen die Kovarianz, die Varianzen und die Standardabweichungen
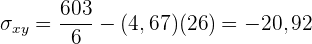
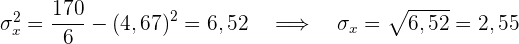
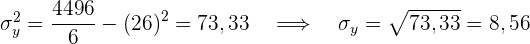
Der Korrelationskoeffizient ist gegeben durch
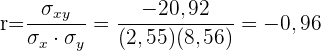
Es besteht eine sehr starke negative Korrelation.
Die Regressionsgerade von Kunden und Entfernung verläuft durch den Punkt und hat die Steigung
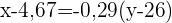
Wir berechnen und erhalten die Regressionsgerade
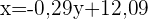
Um die Anzahl der Kunden zu ermitteln, wenn das Einkaufszentrum 2 km entfernt ist, setzen wir 
in die Regressionsgleichung ein und erhalten
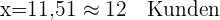
Wenn fünf Kunden angestrebt werden, setzen wir 
in die Regressionsgleichung ein und erhalten
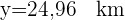
Regressionsgeraden bestimmen
Fünf Schülerinnen und Schüler erzielten in den Fächern Mathematik und Chemie die folgenden Punkte:
| Mathe | Chemie |
|---|---|
|  |
|  |
| |
| |
 | |
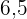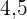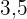Ermittle die Regressionsgeraden und berechne die erwartete Punktzahl in Chemie für einen Schüler, der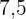 
Punkte in Mathe erreicht hat.
Fünf Schülerinnen und Schüler erzielten in den Fächern Mathematik und Chemie die folgenden Punkte:
| Mathe | Chemie |
|---|---|
| |
| |
| |
| |
| |
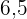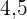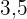Ermittle die Regressionsgeraden und berechne die erwartete Punktzahl in Chemie für einen Schüler, der 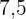Punkte in Mathe erreicht hat.
| | | | |
|---|---|---|---|---|
| | |  |  |
| | |  |  |
| | | |  |
| | | | |
| |  | | |
 |  |  |  | |
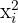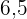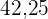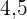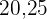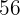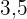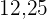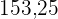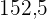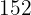Wir berechnen die Durchschnittswerte
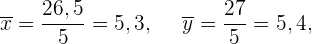
Wir berechnen die Kovarianz und die Varianz von
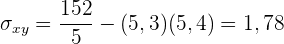
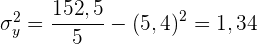
Die Regressionsgerade der Mathe-Punktzahl und der Chemie-Punktzahl verläuft durch den Punkt und hat die Steigung
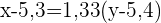
Wir berechnen und erhalten die Regressionsgerade
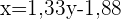
Daraus leiten wir ab und erhalten die Regressionsgerade in Bezug auf die Mathe-Punkte
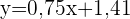
Um die erwartete Punktzahl in Chemie für einen Schüler zu ermitteln, der sieben Punkte in Mathematik hat, setzen wir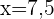 
in die Regressionsgleichung ein und erhalten
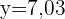
Fundierte Auswahl der Regressionsgeraden
Ein zweidimensionaler Datensatz 
hat den Korrelationskoeffizienten 
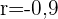, die Mittelwerte der Randverteilungen sind 
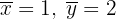. Es ist bekannt, dass eine der folgenden vier Gleichungen der Regressionsgeraden von 
auf 
entspricht:
1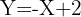 
2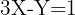 
3 
4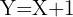 
Nimm eine fundierte Auswahl der Geraden vor.
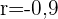Ein zweidimensionaler Datensatz hat den Korrelationskoeffizienten , die Mittelwerte der Randverteilungen sind 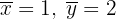. Es ist bekannt, dass eine der folgenden vier Gleichungen der Regressionsgeraden von auf entspricht:
1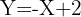
2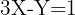
3
4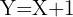
Nimm eine fundierte Auswahl der Gerade vor.
Da der lineare Korrelationskoeffizient negativ ist, ist die Steigung der Geraden ebenfalls negativ. Daher verwerfen wir 
und
Ein Punkt der Geraden muss sein, das heißt 
. Wir setzen in 1 und 3 ein, um zu sehen, welcher Wert die Gleichheit erfüllt
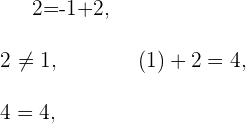
Die gesuchte Gerade ist 3.
Berechnung der Regressionsgeraden
Die Körpergröße und das Gewicht von 
Basketballspielern in einer Mannschaft sind:
Größe  | Gewicht  |
|---|---|
 |  |
 | |
 |  |
 |  |
 |  |
|  |
 |  |
 |  |
 |  |
 |  |
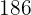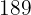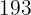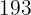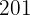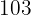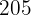Berechne:
1 Die Regeressionsgerade von auf 
.
2 Den Korrelationskoeffizienten.
3 Das geschätzte Gewicht eines Spielers, der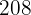 
cm groß ist.
Die Körpergröße und das Gewicht von Basketballspielern in einer Mannschaft sind:
| Größe | Gewicht |
|---|---|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
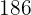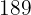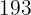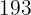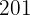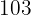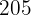Berechne:
1 Die Regressionsgerade von auf .
2 Den Korrlationskoeffizienten.
3 Das geschätzte Gewicht eines Spielers, der 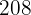cm groß ist.
|  | | | |
|---|---|---|---|---|
| |  |  |  |
| |  | |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| | |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
 |  |  |  |  |
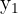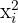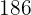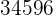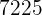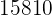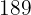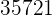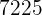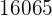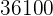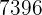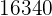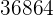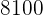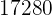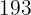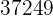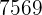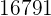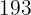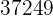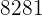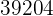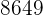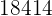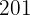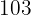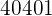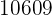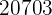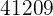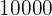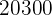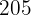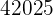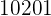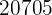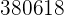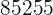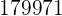Wir berechnen die Durchschnittswerte
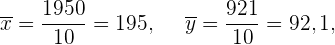
Wir berechnen die Kovarianz, die Varianzen und die Standardabweichungen
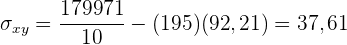
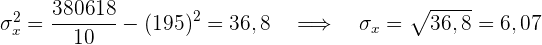
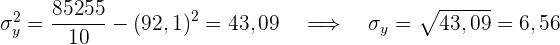
Der Korrelationskoeffizient ist gegeben durch
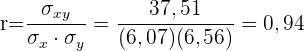
Es besteht eine sehr starke positive Korrelation.
Die Regeressionsgerade von Gewicht und Größe verläuft durch den Punkt und hat die Steigung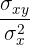 
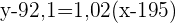
Wir berechnen und erhalten die Regressionsgerade.
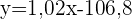
Um das Gewicht eines Spielers mit einer Körpergröße von 208 cm zu ermitteln, setzen wir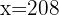 
in die Regressionsgleichung ein und erhalten
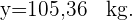
Ermittlung der Regressionsgeraden und des linearen Korrelationskoeffizienten
Bestimme aus den folgenden Daten über die in einer Werkstatt geleisteten Arbeitsstunden und die produzierten Einheiten die Regressionsgerade von auf , den linearen Korrelationskoeffizienten und interpretiere ihn.
| Stunden | Produktion |
|---|---|
 |  |
 |  |
 |  |
 |  |
 | |
|  |
 | |
|  |
| |
| |
|  |
 |  |
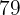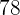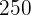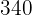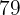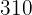Bestimme aus den folgenden Daten über die in einer Werkstatt geleisteten Arbeitsstunden und die produzierten Einheiten die Regressionsgerade von auf , den linearen Korrelationskoeffizienten und interpretiere ihn.
| Stunden | Produktion |
|---|---|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| | | | |
|---|---|---|---|---|
| |  |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| |  | |  |
| |  |  |  |
| |  | |  |
| |  |  |  |
| | | |  |
| | | | |
| | |  |  |
| |  |  |  |
 |  |  |  |  |
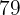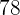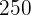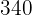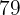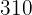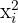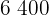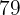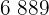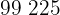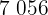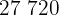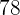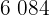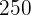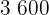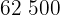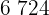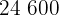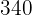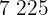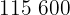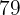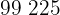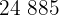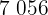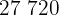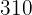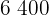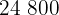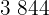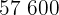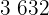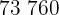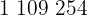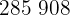Wir berechnen die Durchschnittswerte
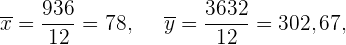
Wir berechnen die Kovarianz, die Varianzen und die Standardabweichungen
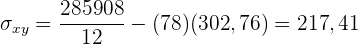
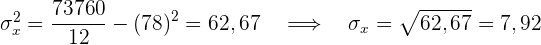
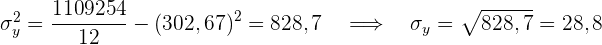
Der Korrelationskoeffizient ist gegeben durch
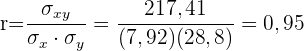
Es besteht eine sehr starke positive Korrelation.
Die Regressionsgerade von auf verläuft durch den Punkt und hat die Steigung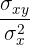
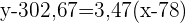
Wir berechnen und erhalten die Regressionsgerade
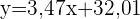
Berechnung des Korrelationskoeffizienten und Bestimmung der Geradengleichung
Eine Gruppe von 
Personen wurde gebeten, Angaben zur Anzahl der Stunden zu machen, die sie täglich mit Schlafen und Fernsehen verbringen. Anhand der Klassifizierung der Antworten kann folgende Tabelle erstellt werden:
| Anzahl der Stunden - Schlaf | | | | | |
|---|---|---|---|---|---|
| Anzahl der Stunden - Fernsehen | | | | | |
Absolute Häufigkeiten  | | | | | |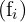
Wir möchten:
1 Den Korrelationskoeffizienten berechnen.
2 Die Gleichung der Regressionsgeraden von auf bestimmen.
3 Wenn ein Mensch 8,5 Stunden schläft, wie viel kann er oder sie dann noch fernsehen?
Eine Gruppe von Personen wurde gebeten, Angaben zur Anzahl der Stunden zu machen, die sie täglich mit Schlafen und Fernsehen verbringen. Anhand der Klassifizierung der Antworten kann folgende Tabelle erstellt werden:
| Anzahl der Stunden - Schlaf | | | | | |
|---|---|---|---|---|---|
| Anzahl der Stunden - Fernsehen | | | | | |
| Absolute Häufigkeiten | | | | | |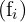
Wir möchten:
1 Den Korrelationskoeffizienten berechnen.
2 Die Gleichung der Regressionsgeraden von auf bestimmen.
3 Wenn ein Mensch 8,5 Stunden schläft, wie viel kann er oder sie dann noch fernsehen?
| |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|
| | | |  |  |  |  |
| | |  |  | |  |  |
| | | |  | |  |  |
| | | |  | | | |
| | | | | | | |
|  |  |  |  |  |
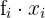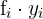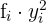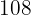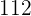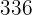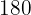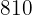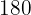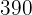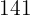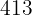Wir berechnen die Durchschnittswerte
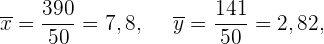
Wir berechnen die Kovarianz, die Varianzen und die Standardabweichungen
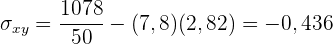
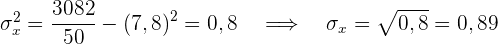
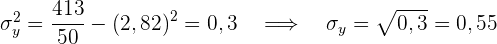
Der Korrelationskoeffizient ist gegeben durch
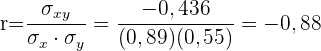
Es besteht eine starke negative Korrelation.
Die Regressionsgerade von auf verläuft durch den Punkt und hat die Steigung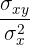
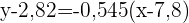
Wir berechnen und erhalten die Regressionsgerade
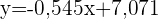
Um die Anzahl der Stunden zu ermitteln, die eine Person, die 8,5 Stunden schläft, fernsieht, setzen wir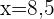 
in die Regressionsgleichung ein und erhalten
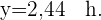
Bestimmung des Korrelationskoeffizienten und Berechnung der Regressionsgeraden
In der nachstehenden Tabelle sind die Ergebnisse der Eignungstests von sechs Probezeitbewerber*innen und die Umsätze des ersten Monats der Probezeit in Hunderten von Euro angegeben.
| | |  |  |  | |
|---|---|---|---|---|---|---|
| | | | |  | |
1 Ermittle den Korrelationskoeffizienten und interpretiere das erhaltene Ergebnis..
2 Berechne die Regressionsgerade von auf .
3 Sag den Umsatz eines Verkäufers oder einer Verkäuferin voraus, der/die in dem Test 
Punkte erzielt.
Die folgende Tabelle enthält die Ergebnisse der Eignungstests von sechs Probezeitbewerber*innen und den Umsatz des ersten Monats der Probezeit in Hunderten von Euro.
| | | | | | |
|---|---|---|---|---|---|---|
| | | | | | |
1 Ermittle den Korrelationskoeffizienten und interpretiere das erhaltene Ergebnis.
2 Berechne die Regressionsgerade von auf .
3 Sag den Umsatz eines Verkäufers oder einer Verkäuferin voraus, der/die in dem Test Punkte erzielt.
| | | | |
|---|---|---|---|---|
| | |  |  |
| | |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
| |  |  |  |
 |  |  |  |  |
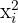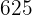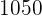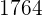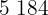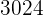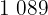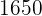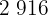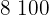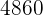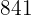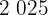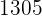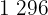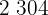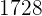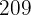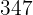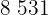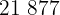Wir berechnen die Durchschnittswerte
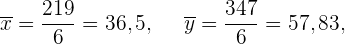
Wir berechnen die Kovarianz, die Varianzen und die Standardabweichungen
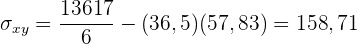
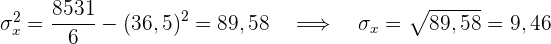
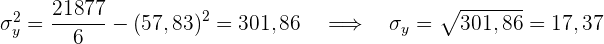
Der Korrelationskoeffizient ist gegeben durch
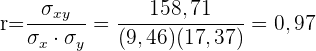
Es besteht eine sehr starke positive Korrelation.
Die Regressionsgerade von auf verläuft durch den Punkt und hat die Steigung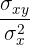
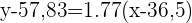
Wir berechnen und erhalten die Regressionsgerade
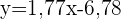
Um den Umsatz eines Verkäufers oder einer Verkäuferin vorherzusagen, der/die im Test 47 Punkte erzielt, setzen wir 
in die Regressionsgleichung ein und erhalten
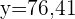
Bestimmung des Korrelationskoeffizienten und Berechnung der Regressionsgeraden II
Die folgende Tabelle zeigt die Beziehung zwischen der durchschnittlichen monatlichen Temperatur (T) in 
einer bestimmten Stadt und dem monatlichen Eiscremeumsatz in Tausend Dollar (D).
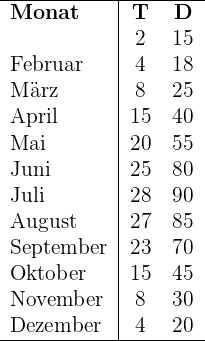
1 Ermittle die Regressionsgerade des monatlichen Umsatzes in Abhängigkeit von der Durchschnittstemperatur jedes Monats.
2 Berechne den linearen Korrelationskoeffizienten und interpretiere das Ergebnis.
3 Wie viele Tausend Dollar würden nach der Regressionsgeraden in einem Monat mit einer Durchschnittstemperatur von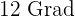 
verkauft werden?
4 Wäre es für einen örtlichen Eisstand sinnvoll, in einem Monat mit einer Durchschnittstemperatur von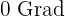 
5.000 $ zu investieren?
1
Wir möchten die reellen Zahlen 
und 
so bestimmen, dass wir 
so nah wie möglich an die Gerade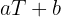 
schreiben können. Zunächst berechnen wir die Summe der Werte 
und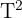 
.
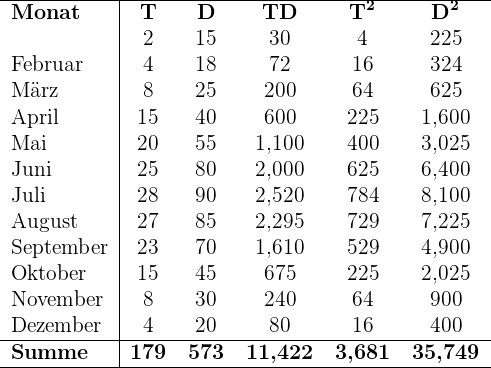
Wir berechnen nun die Durchschnittswerte, die Kovarianz und die Standardabweichungen::
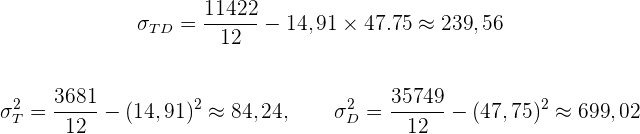
Das heißt
Daraus schließen wir, dass
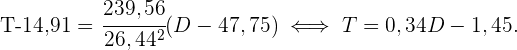
2 Der lineare Korrelationskoeffizient ist gegeben durch
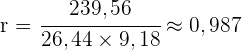
Das heißt, dass der monatliche Eisverkauf eine starke positive Korrelation mit der Durchschnittstemperatur des jeweiligen Monats aufweist.
3 Wir möchten den Wert für bestimmen
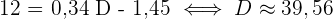
Somit ist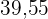 
der Wert, den unsere Regressionsgerade in einem Monat mit einer Durchschnittstemperatur von 
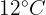erwartet.
4 Nach unserer Regressionsgeraden würde der Umsatz mit Eis in einem Monat bei dieser Temperatur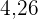 
Tausend Dollar betragen. Das heißt, dass eine Investition, die diesen Betrag übersteigt, zu einem Gewinnverlust führt. Daher ist es nicht im Interesse der Eisdiele, diese 5.000 Dollar zu investieren.
Berechnung der Kovarianz und des Korrelationskoeffizienten für eine große Inhaltstabelle
Die folgende Tabelle zeigt den Zusammenhang zwischen dem höchsten Bildungsgrad einer Person und der Wahrscheinlichkeit, sich in einem bestimmten jährlichen Einkommensbereich zu befinden (in Tausend Dollar)
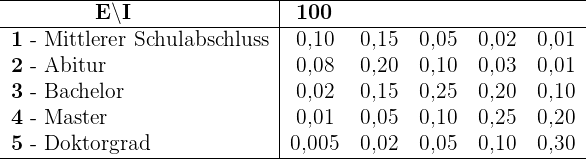
1 Berechne die Kovarianz, die Standardabweichung und die Durchschnittswerte.
2 Berechne den Korrelationskoeffizienten.
1
Wir wandeln die gegebene Tabelle in eine einfachere Tabelle um. Der Bereich 
als und die anderen Bereiche werden durch den Durchschnittswert der Grenzpunkte dargestellt.
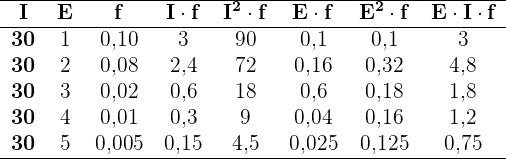
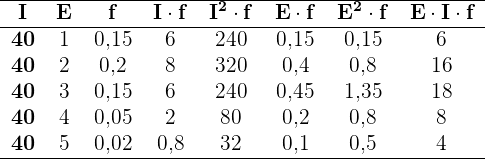
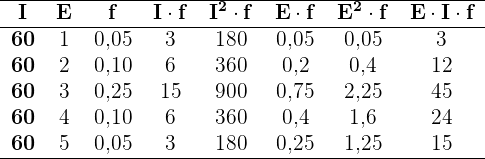
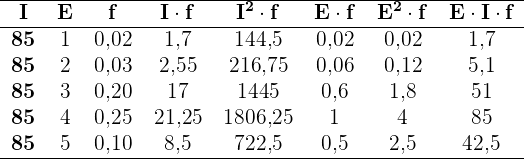
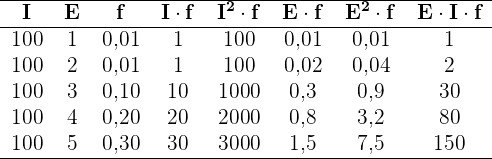
Addiert man alle Werte der erforderlichen Spalten, erhält man
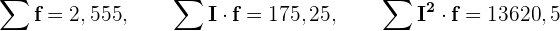
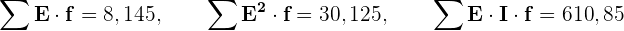
Außerdem:
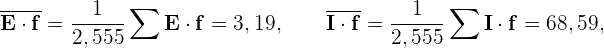
und die Kovarianz ist
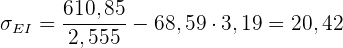
2
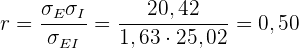
Es besteht also eine mäßige Korrelation.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
