Kapitel
Zur Erinnerung: die Variation einer Gesamtzahl von  Objekten, die in Gruppen von jeweils
Objekten, die in Gruppen von jeweils  Objekten ausgewählt werden, wird mit der folgenden Formel berechnet:
Objekten ausgewählt werden, wird mit der folgenden Formel berechnet:
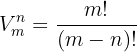
Dabei ist 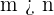 .
.
Gleichermaßen wird die Variation mit Wiederholung einer Gesamtmenge von  Objekten, aus denen
Objekten, aus denen  Objekte ausgewählt werden, anhand der folgenden Formel berechnet:
Objekte ausgewählt werden, anhand der folgenden Formel berechnet:
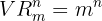
Dabei ist 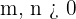 . Es gibt keine Restriktionen.
. Es gibt keine Restriktionen.
Mithilfe dieser Definitionen gehen wir nun zum Aufgabenteil über.

Rechenbeispiele: Zahlen
Wieviele Zahlen aus jeweils drei unterschiedlichen Ziffern kann man mit den Zahlen  bilden?
bilden?
Hier handelt es sich um eine Variation, denn:
1 Nicht alle Elemente sind Teil der Betrachtung. Es werden nur drei der fünf Zahlen beachtet.
2 Die Reihenfolge ist wichtig. Es ist nicht dasselbe, die Zahlen in der Reihenfolge  oder
oder  aufzuschreiben.
aufzuschreiben.
3 Die Elemente wiederholen sich nicht. Sobald eine Zahl für eine der drei Positionen ausgewählt wurde, ist diese nicht mehr Bestandteil für die anderen Auswahlen. Alle Ziffern müssen unterschiedlich sein.
Wir erhalten also Variationen von  Elementen, die in
Elementen, die in  er-Gruppen ausgewählt werden, d.h.
er-Gruppen ausgewählt werden, d.h.  und
und  . Die Anzahl der verschiedenen Zahlen, die wir mit den Ziffern bilden können ist daher
. Die Anzahl der verschiedenen Zahlen, die wir mit den Ziffern bilden können ist daher
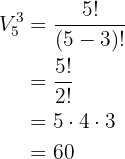
Wieviele Zahlen aus jeweils drei unterschiedlichen Ziffern kann man mit den Zahlen  bilden, wenn sich die Ziffern wiederholen dürfen
bilden, wenn sich die Ziffern wiederholen dürfen
Hier handelt es sich um eine Variation, denn:
1 Nicht alle Elemente sind Teil der Betrachtung. Es werden nur 3 aus 5 Zahlen ausgewählt.
2 Die Reihenfolge ist wichtig. Es ist nicht dasselbe, die Zahlen in der Reihenfolge  oder
oder  aufzuschreiben.
aufzuschreiben.
3 Die Elemente wiederholen sich. Es dürfen zum Beispiel Zahlen wie 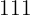 ,
, 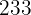 ,
, 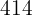 , etc. gebildet werden.
, etc. gebildet werden.
Wir erhalten also Variationen mit Wiederholung von  Elementen, die in
Elementen, die in  er-Gruppen ausgewählt werden, d.h
er-Gruppen ausgewählt werden, d.h  y
y  . Die Anzahl der verschiedenen Zahlen, die wir mit den Ziffern bilden können ist daher
. Die Anzahl der verschiedenen Zahlen, die wir mit den Ziffern bilden können ist daher
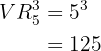
Wieviele Zahlen bestehend aus drei Ziffern kann man mit den Zahlen  bilden?
bilden?
Diese Aufgabe ist etwas komplexer, da die erste Zahl größer als Null sein muss, daher gibt es für die erste Ziffer  mögliche Elemente zur Auswahl (
mögliche Elemente zur Auswahl (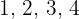 und
und  ), das heißt wir erhalten Variationen von
), das heißt wir erhalten Variationen von  Elementen, die
Elementen, die  er-Gruppen ausgewählt werden
er-Gruppen ausgewählt werden
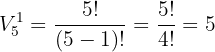
Sobald die Ziffer für die erste Position ausgewählt wurde, bleiben noch  Zahlen übrig plus die Zahl
Zahlen übrig plus die Zahl  , da diese an zweiter Position stehen darf, daher haben wir wieder
, da diese an zweiter Position stehen darf, daher haben wir wieder  Möglichkeiten zur Auswahl. Für die zweite und dritte Ziffer stehen uns also 5 Zahlen zur Auswahl mit der Restriktion, dass sie sich nicht wiederholen dürfen. Daher erhalten wir Variationen von
Möglichkeiten zur Auswahl. Für die zweite und dritte Ziffer stehen uns also 5 Zahlen zur Auswahl mit der Restriktion, dass sie sich nicht wiederholen dürfen. Daher erhalten wir Variationen von  Objekten insgesamt, die in
Objekten insgesamt, die in  er-Gruppen ausgewählt werden.
er-Gruppen ausgewählt werden.
1 Nicht alle Elemente sind Teil der Betrachtung. Nur zwei aus fünf Zahlen werden betrachtet.
2 Die Reihenfolge ist wichtig. Es ist nicht dasselbe, ob man  oder
oder  wählt.
wählt.
3 Die Elemente wiederholen sich nicht. Alle Ziffern müssen unterschiedlich sein.
Für die Berechnung der Variationen ist  und
und 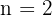 .
.
Wir erhalten unsere Lösung also, indem wir die Variationen der ersten Ziffer mit denen der zweiten und dritten Ziffer multiplizieren
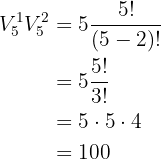
Wieviele Zahlen aus jeweils drei unterschiedlichen Ziffern kann man mit den Zahlen  , wenn sich die Ziffern wiederholen dürfen?
, wenn sich die Ziffern wiederholen dürfen?
Wie beim vorherigen Beispiel ist diese Augabe etwas komplexer, da die erste Ziffer nicht Null sein kann. Daher gibt es  Optionen für die erste Ziffer und zwar
Optionen für die erste Ziffer und zwar 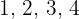 und
und  . Wir erhalten Variationen von
. Wir erhalten Variationen von  Elementen aus denen jeweils
Elementen aus denen jeweils  Element ausgewählt wird
Element ausgewählt wird
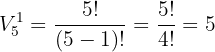
Sobald die erste Ziffer entschieden wurde, steht uns jede beliebige der sechs Zahlen zur Verfügung, sowohl für die zweite, als auch für die dritte und alle fortfolgenden Positionen. Die Ziffern dürfen sich außerdem wiederholen, das heißt, wir erhalten Variationen mit Wiederholungen von  Elementen, aus denen
Elementen, aus denen  Elemente ausgewählt werden
Elemente ausgewählt werden
1 Nicht alle Elemente sind Teil der Betrachtung. Nur zwei aus fünf Zahlen werden betrachtet.
2 Die Reihenfolge ist wichtig. Es ist nicht dasselbe, ob man  oder
oder  wählt.
wählt.
3 Die Elemente wiederholen sich.
Für diese Variationen mit Wiederholung gilt 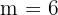 und
und 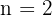 .
.
Wir erhalten unsere Lösung also, indem wir die Variationen der ersten Ziffer mit den Variationen mit Wiederholung der zweiten und dritten Ziffer multiplizieren
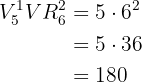
Wieviele Zahlen aus jeweils fünf unterschiedlichen Ziffern kann man mit den Zahlen 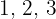 bilden?
bilden?
Es soll eine fünfstellige Zahl aus drei Ziffern gebildet werden, wobei jede Ziffer eine der fünf möglichen Positionen einnehmen kann, d.h. wir gehen davon aus, dass sich die Elemente wiederholen dürfen (wenn sie sich nicht wiederholen dürften, könnten nur drei der fünf Stellen besetzt werden und es käme keine fünfstellige Zahl zustande). Folgende Bedingungen werden erfüllt
1 Alle Elemente werden in die Auswahl mit einbezogen
2 Die Reihenfolge ist wichtig. Es ist nicht dasselbe,  oder
oder  aufzuschreiben.
aufzuschreiben.
3 Die Elemente wiederholen sich.
Wie erhalten also Variationen mit Wiederholung von  Elementen, die
Elementen, die  Elemente verteilt werden, d.h.
Elemente verteilt werden, d.h. 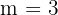 ,
,  . Die Menge der Zahlen, die man so bilden kann wird also wie folgt bestimmt:
. Die Menge der Zahlen, die man so bilden kann wird also wie folgt bestimmt:
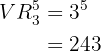
Rechenbeispiele: Sportarten
Wieviele Wettscheine mit einer Spalte muss man ausfüllen, um bei einem Fußball-Wettspiel  richtige Ergebnisse zu erhalten?
richtige Ergebnisse zu erhalten?
Lasst uns zuerst das Wettspiel erklären: Auf jedem Wettschein ist eine Spalte mit  Fußballspielen aufgelistet. Bei jedem Spiel gibt es
Fußballspielen aufgelistet. Bei jedem Spiel gibt es  mögliche Ergebnisse: die Mannschaft, die links steht, gewinnt, die Mannschaft, die rechts steht, gewinnt, oder es gibt ein Unentschieden.. Wir erhalten also Variationen mit Wiederholungen, bei denen
mögliche Ergebnisse: die Mannschaft, die links steht, gewinnt, die Mannschaft, die rechts steht, gewinnt, oder es gibt ein Unentschieden.. Wir erhalten also Variationen mit Wiederholungen, bei denen 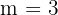 ,
, 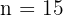 und
und 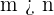 ist. Außerdem gelten folgende Bedingungen:
ist. Außerdem gelten folgende Bedingungen:
1 Alle Elemente sind Teil der Betrachtung.
2 Die Reihenfolge ist wichtig. Es ist nicht dasselbe, ob die rechte oder die linke Mannschaft gewinnt.
3 Die Elemente wiederholen sich.
Die Zahl der Wettscheine, die man ausfüllen muss, um sich 15 Treffer zu sichern ist also:
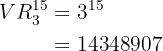
Wieviele Fußballspiele finden bei einer Liga statt, an der 4 Mannschaften teilnehmen?
Folgende Bedingungen werden erfüllt:
1 Alle Elemente sind Teil der Betrachtung.
2 Die Reihenfolge ist wichtig. Da die Mannschaft, die links steht, immer als "Gastgeber" und die Mannschaft, die rechts steht, als "Gast" verstanden wird, ist es nicht dasselbe, ob A gegen B oder B gegen A spielt.
3 Die Elemente wiederholen sich nicht. Ein Spiel von Mannschaft A gegen Mannschaft A kann es nicht geben.
Wir erhalten also Variationen mit  und
und 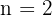 . Die Spiele, die insgesamt stattfinden können, sind also:
. Die Spiele, die insgesamt stattfinden können, sind also:
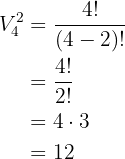
Auf wieviele verschiedene Arten können die Stellen des Präsidenten, Vizepräsidenten und Schatzmeisters eines Fußballclubs besetzt werden, wenn  Personen dafür kandidieren?
Personen dafür kandidieren?
Folgende Bedingungen werden erfüllt:
1 Alle Elemente sind Teil der Betrachtung.
2 Die Reihenfolge ist wichtig. Es macht einen Unterschied, ob Peter Präsident und Jochen Vizepräsident ist oder umgekehrt.
3 Die Elemente wiederholen sich nicht. Eine Person kann nicht zwei Posten gleichzeitig besetzen.
Wir erhalten also Variationen, bei denen 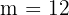 und
und  ist. Die Zahl der verschiedenen Arten, wie die drei Positionen besetzt werden können, erhält man also wie folgt:
ist. Die Zahl der verschiedenen Arten, wie die drei Positionen besetzt werden können, erhält man also wie folgt:
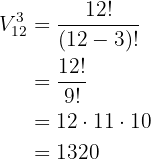
Rechenbeispiele: Gemischte Themen
 Kandidaten haben sich mit ihren Romanen für einen Literaturwettbewerb angemeldet. Auf die Ehrenliste kommen der Sieger, der Zweit- und der Drittplatzierte. Wieviele Möglichkeiten gibt es, die Ehrenliste zu bilden?
Kandidaten haben sich mit ihren Romanen für einen Literaturwettbewerb angemeldet. Auf die Ehrenliste kommen der Sieger, der Zweit- und der Drittplatzierte. Wieviele Möglichkeiten gibt es, die Ehrenliste zu bilden?
Folgende Bedingungen werden erfüllt:
1 Alle Elemente sind Teil der Betrachtung.
2 Die Reihenfolge ist wichtig. Es macht einen Unterschied, ob Maria gewinnt und Teresa zweite wird oder umgekehrt.
3 Die Elemente wiederholen sich nicht. Eine Person kann nicht zwei der Plätze besetzen.
Wir erhalten also Variationen bei denen 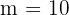 und
und  ist. Es gibt also folgende Möglichkeiten, die Plätze zu besetzen:
ist. Es gibt also folgende Möglichkeiten, die Plätze zu besetzen:
Wie viele verschiedene Signale können mit den Zeichen des Morse-Systems (Punkt / Strich) mit maximal vier Tastenanschlägen gesendet werden?
Da vier Tastenschläge getätigt werden sollen, müssen wir die Möglichkeiten für jeden einzelnen Tastenschlag einzeln betrachten und alle miteinander summieren.
Für den ersten Tastenschlag können wir entweder Punkt oder Strich als Ergebnis erhalten.
Für alle darauffolgenden Tastenschläge gilt Folgendes:
1 Alle Elemente sind Teil der Betrachtung.
2 Die Reihenfolge ist wichtig.
3 Die Elemente wiederholen sich. Punkte oder Striche können direkt hintereinander oder abwechselnd erfolgen
Bei zwei Tastenschlägen erhalten wir also folgende Anzahl an verschiedenen möglichen Zeichen:
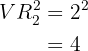
Bei drei Tastenschlägen erhalten wir folgende Anzahl an möglichen Zeichen:
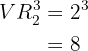
Bei vier Tastenschlägen erhalten wir folgende Anzahl an möglichen Zeichen:
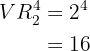
Für maximal vier Tastenschläge ist die Gesamtzahl an möglichen gesendeten Zeichen also:
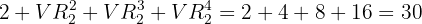
Wieviele Palindromzahlen aus acht Ziffern gibt es?
Eine Palindromzahl ist eine Zahl, die vorwärts und rückwärts gelesen genau gleich ist. Sie hat also folgende Form:
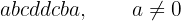
wobei  und
und  ihre Ziffern beschreiben. Bei dieser Aufgabe geht es also in Wirklichkeit darum, zu bestimmen, auf wieviele mögliche Arten Zahlen mit
ihre Ziffern beschreiben. Bei dieser Aufgabe geht es also in Wirklichkeit darum, zu bestimmen, auf wieviele mögliche Arten Zahlen mit  Ziffern anhand der Zahlen von
Ziffern anhand der Zahlen von  bis
bis  (also 10 Zahlen) geformt werden können.
(also 10 Zahlen) geformt werden können.  muss dabei ungleich
muss dabei ungleich  sein.
sein.  und
und  können jeden beliebigen Wert annehmen und sich auch wiederholen, das heißt
können jeden beliebigen Wert annehmen und sich auch wiederholen, das heißt  darf gleich
darf gleich  sein.
sein.
Wie gehen wir die Aufgabe nun an? Im Grunde ist der Rechenweg derselbe wie in Aufgabe  . Schau dir zuerst den Fall von
. Schau dir zuerst den Fall von  an. Für
an. Für  gibt es
gibt es  verschiedene Optionen, da
verschiedene Optionen, da  nicht mitgezählt werden darf.
nicht mitgezählt werden darf.
Für  ,
,  und
und  gibt es
gibt es  Möglichkeiten, d.h. wir erhalten Variationen mit Wiederholung, bei denen
Möglichkeiten, d.h. wir erhalten Variationen mit Wiederholung, bei denen 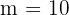 und
und  ist. Es gilt:
ist. Es gilt:
1 Alle Elemente sind Teil der Betrachtung.
2 Die Reihenfolge ist wichtig.
3 Die Elemente wiederholen sich.
Die unterschiedlichen Möglichkeiten für  ,
,  und
und  wird also wie folgt ermittelt:
wird also wie folgt ermittelt:
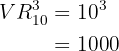
Um die Zahl der möglichen Palindrome aus  Ziffern zu erhalten, multiplizieren wir einfach die Anzahl der Möglichkeiten für die erste Ziffer mit der Zahl der Möglichkeiten für die zweite, dritte und vierte Ziffer:
Ziffern zu erhalten, multiplizieren wir einfach die Anzahl der Möglichkeiten für die erste Ziffer mit der Zahl der Möglichkeiten für die zweite, dritte und vierte Ziffer:
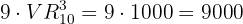
Kombinationsgleichungen
Löse auf
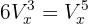
Um die Gleichung zu lösen, wenden wir die Formel für Variationen an
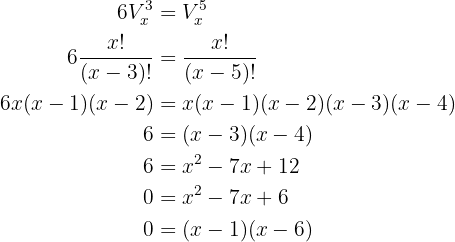
Die Lösungen sind also  und
und  . Da
. Da 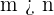 sein muss, muss
sein muss, muss  größer als
größer als  und als
und als  sein, daher ist die einzig mögliche Lösung
sein, daher ist die einzig mögliche Lösung  .
.
Löse auf
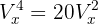
Um die Gleichung zu lösen, wenden wir die Formel für Variationen an
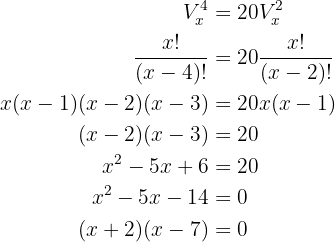
Die Lösungen sind also  und
und  . Da
. Da 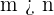 sein muss, muss
sein muss, muss  größer als
größer als  und als
und als  sein, daher ist die einzig mögliche Lösung
sein, daher ist die einzig mögliche Lösung  (
( darf außerdem nicht negativ sein).
darf außerdem nicht negativ sein).
Löse auf

Um die Gleichung zu lösen, wenden wir die Formel für Variationen an
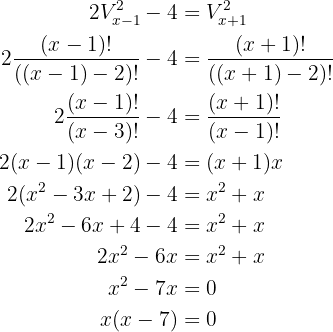
Die Lösungen sind  und
und  . Da
. Da  sein muss, muss
sein muss, muss  größer als
größer als  sein, daher ist die einzige Lösung
sein, daher ist die einzige Lösung  (
( darf außerdem nicht gleich
darf außerdem nicht gleich  sein).
sein).
Löse auf

Um die Gleichung zu lösen, wenden wir die Formel für Variationen an
Die Lösungen sind  und
und  . Da
. Da 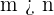 sein muss, muss
sein muss, muss  größer als
größer als  sein, daher ist die einzige Lösung
sein, daher ist die einzige Lösung  (
( darf außerdem nicht gleich
darf außerdem nicht gleich  sein).
sein).
Löse auf

Wende die Formel für Variationen und Variationen mit Wiederholungen an:
In diesem Fall gibt es nur eine Lösung und zwar 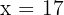 .
.
Mit KI zusammenfassen:













