Eine Variation mit Wiederholung sind die verschiedenen Möglichkeiten, wie eine Auswahl von Elementen aus einer gegebenen Menge getroffen werden kann, so dass die ausgewählten Elemente wiederholt werden können.

Merkmale der Variation mit Wiederholung
- Sie hat insgesamt m Elemente und wird andererseits zu einer Gruppe von n Positionen gebildet.
- Nun kann jedes der m Elemente an jeder Position platziert werden, was bedeutet, dass zwei oder mehr Positionen für dasselbe Element wiederholt werden können.
- Jede gebildete Gruppe unterscheidet sich von einer anderen, wenn sich ein Element an einer beliebigen Position unterscheidet. Zum Beispiel unterscheidet sich die 3-Positionen-Gruppe 831 von einer anderen 3-Positionen-Gruppe 821, weil in der zweiten Position jeder von ihnen verschiedene Elemente vorhanden sind – 3 ist nämlich anders als 2.
- Die Gruppe mit 4 Positionen, z. B. 4523, unterscheidet sich von der Gruppe 4253, da die Reihenfolge der Platzierung unterschiedlich ist, obwohl es sich um dieselben Elemente handelt.
Das heißt, wenn Gruppen mit diesen Merkmalen gebildet werden, gilt Folgendes:
- Die Reihenfolge spielt eine Rolle.
- Die Elemente werden wiederholt.
Die Gesamtzahl der Gruppen der Größe n, die mit m Elementen unter Berücksichtigung von Wiederholungen gebildet werden können, wird durch folgende Formel berechnet:

Sie kann auch wie folgt geschrieben werden: 
Beispiele für Variationen mit Wiederholungen
1 Wie viele dreistellige Zahlen können mit den Ziffern 1, 2, 3, 4, 5 gebildet werden?
Hier können wir sehen, dass es fünf Elemente m = 5 in drei Positionen n = 3 gibt:
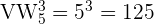
Mit den angegebenen Ziffern lassen sich also 125 dreistellige Zahlen bilden. Beachte, dass die Reihenfolge eine Rolle spielt, da z. B. 123 sich von 132 unterscheidet, und dass eine Wiederholung möglich ist, da die Zahl 223 eine der 125 möglichen Zahlen ist, die man bilden kann.
2 Wie viele dreistellige Zahlen können mit den Ziffern 0, 1, 2, 3, 4, 5 gebildet werden?
Wir möchten dreistellige Zahlen bilden. Allerdings kann die erste Zahl nicht mit einer 0 beginnen, da eine 0 am Anfang keinen Unterschied macht (01 ist gleich 1), also können wir in der ersten Zahl nur 1 bis 5 einsetzen, also m=5 und n=1.
Wenn wir dagegen 0 bis 5 in die nächsten beiden Ziffern der Zahl einsetzen können, dann ist m=6 und n=2.
Berechnet man schließlich die Variationen für jeden Fall und multipliziert sie miteinander, erhält man die Lösung
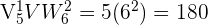
3 Wenn ein Fragebogen 15 Fragen enthält und jede Frage drei Antwortmöglichkeiten hat, wie viele verschiedene Möglichkeiten gibt es, den Fragebogen zu lösen?
Die Werte von m = 3 und n = 15 ergeben die Gesamtzahl der möglichen Kombinationen zur Lösung des Fragebogens:
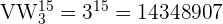
Es gibt also 14 348 907 verschiedene Möglichkeiten, den Fragebogen zu lösen.
Zusammenfassend lässt sich sagen, dass es verschiedene Probleme gibt, bei denen es notwendig ist, die Gesamtzahl der möglichen Kombinationen zu berechnen, und dass die Art und Weise der Berechnung manchmal sehr kompliziert sein kann. Deshalb gibt es Werkzeuge zum Zählen, wie z. B. Variationen mit Wiederholung.
Mit KI zusammenfassen:












