Die Kombinatorik ist ein Teilgebiet der Mathematik, das sich mit der Anordnung oder Gruppierung einer Anzahl von Elementen oder Objekten befasst. Dies kann sehr nützlich sein, um die möglichen und günstigen Ereignisse zu berechnen und dann die Laplace-Regel anzuwenden.
Um die Kombinatorik in der Wahrscheinlichkeitsrechnung anwenden zu können, müssen wir zunächst die Grundbegriffe der Kombinatorik kennen, wie Permutationen, Variationen usw.

Konzepte der Kombinatorik
Variationen
Die verschiedenen Gruppen, die von  Elementen gebildet werden, werden Variationen von
Elementen gebildet werden, werden Variationen von  Elementen aus
Elementen aus  in
in 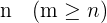 genannt, wobei:
genannt, wobei:
- Die Reihenfolge spielt eine Rolle.
- Die Elemente wiederholen sich nicht.
Variationen werden wie folgt notiert:
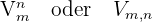
Die Formel zur Berechnung ist gegeben durch

Wir können uns Variationen als eine Menge mit  Objekten vorstellen. Aus dieser Menge nehmen wir alle Teilmengen mit
Objekten vorstellen. Aus dieser Menge nehmen wir alle Teilmengen mit  Objekten. Danach ordnen wir jede Teilmenge auf alle möglichen Arten.
Objekten. Danach ordnen wir jede Teilmenge auf alle möglichen Arten.
Permutationen
Permutationen von  Elementen sind die verschiedenen Möglichkeiten, wie diese
Elementen sind die verschiedenen Möglichkeiten, wie diese  Elemente angeordnet werden können. Hierbei ist zu beachten:
Elemente angeordnet werden können. Hierbei ist zu beachten:
- Die Reihenfolge spielt eine Rolle, da der Austausch zweier verschiedener Elemente eine neue Permutation ergibt.
- Die Elemente werden nicht wiederholt, denn wenn sie sich wiederholen oder gleich sind, führt ihr Austausch nicht zu einer neuen Permutation.
Die folgende Formel wird verwendet, um die Gesamtzahl der Permutationen von m Elementen zu erhalten:

Kombinationen
Alle Gruppierungen, die mit  Elementen gebildet werden können, werden Kombinationen von
Elementen gebildet werden können, werden Kombinationen von  Elementen aus
Elementen aus  in
in 
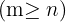 genannt. Hierbei ist zu beachten:
genannt. Hierbei ist zu beachten:
- Nicht alle Elemente werden in Betracht gezogen.
- Die Reihenfolge spielt keine Rolle.
- Die Elemente wiederholen sich nicht.
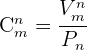
Wir können Kombinationen auch mithilfe von Fakultäten berechnen:
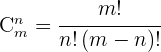
Kombinationen werden als 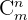 oder
oder 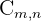 notiert.
notiert.
Kombinatorik bei der Wahrscheinlichkeit
Die Kombinatorik kann sehr nützlich sein, um bei der Anwendung der Laplace-Regel die möglichen und günstigen Ereignisse zu berechnen. Vor allem, wenn es eine große Anzahl von Ereignissen gibt.
Beispiele
1. Eine Gruppe von  Personen sitzt auf einer Bank. Wie groß ist die Wahrscheinlichkeit, dass zwei im Voraus festgelegte Personen zusammensitzen?
Personen sitzt auf einer Bank. Wie groß ist die Wahrscheinlichkeit, dass zwei im Voraus festgelegte Personen zusammensitzen?
- Mögliche Fälle:Es ist die Anzahl der verschiedenen Möglichkeiten, wie
 Personen angeordnet werden können.
Personen angeordnet werden können.
- Günstige Fälle:Wenn wir die beiden zusammensitzenden Personen als eine Person betrachten, sind es
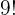 ; aber sie können entweder links oder rechts voneinander sitzen, sodass man
; aber sie können entweder links oder rechts voneinander sitzen, sodass man 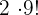 erhält.
erhält.
Wir berechnen also wie folgt

2. Berechne die Wahrscheinlichkeit, dass beim Ziehen von 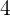 Karten (eine nach der anderen) aus einem Kartenspiel mit
Karten (eine nach der anderen) aus einem Kartenspiel mit 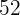 Karten nur Asse gezogen werden.
Karten nur Asse gezogen werden.
- Günstige Fälle:Dies sind die verschiedenen Reihenfolgen, in denen die
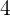 Asse gezogen werden könnten.
Asse gezogen werden könnten.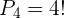
- Mögliche Fälle:Dies sind die verschiedenen Gruppen von
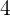 Karten, die wir aus den
Karten, die wir aus den  Karten erhalten könnten.
Karten erhalten könnten.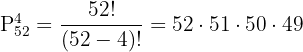
Wir berechnen also wie folgt
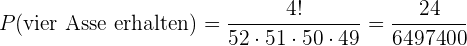
Mit KI zusammenfassen:












