Vereinigung von Ereignissen
Gegeben sind zwei Ereignisse 
und 
. Wir definieren die Vereinigung der Ereignisse, angegeben mit 
, als das Ereignis, das aus allen Elementen besteht, die zu oder zu gehören. Das heißt, das Ereignis 
tritt ein, wenn eines der beiden Ereignisse, oder , oder beide eintreten.
wird als " vereinigt mit " gelesen.
Beobachtung. Wir stellen fest, dass die Vereinigung zweier Ereignisse in Wirklichkeit nichts anderes ist, als die Vereinigung ihrer Mengen.
Beispiel:
Betrachten wir das Experiment, bei dem ein Würfel geworfen wird, betrachten wir das Ereignis, dass eine gerade Zahl gewürfelt wird, als 
und das Ereignis, dass eine Zahl gewürfelt wird, die ein Vielfaches von drei ist, als 
. Wir berechnen die Vereinigung der Ereignisse und 
():
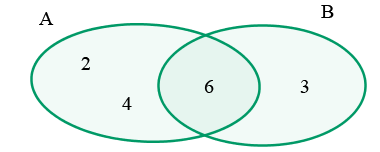
Wahrscheinlichkeit der Vereinigung von Ereignissen
Wir betrachten zwei Ereignisse und mit den Wahrscheinlichkeiten 
und 
. Also ist die Wahrscheinlichkeit ihrer Ereignisse, , gegeben durch
.
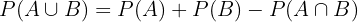
Dies ergibt zwei wichtige Fälle, die zu berücksichtigen sind. Wenn 
und wenn 
.
Wahrscheinlichkeit der Vereinigung vereinbarer Ereignisse
Wir sagen, dass zwei Ereignisse und vereinbar sind, wenn sie mindestens ein gemeinsames Elementareignis enthalten. Mit anderen Worten, wenn beide mindestens ein gemeinsames Ergebnis berücksichtigen.
Wenn zwei Ereignisse und vereinbar sind, ist ihre Schnittmenge nicht leer (sie unterscheidet sich von der leeren Menge 
). Das heißt
.
Da in diesem Fall die Schnittmenge nicht leer ist und ihre Elemente (das betrachtete Ergebnis) zum Stichprobenraum gehören, gilt 
. Wir betrachten also die Gleichung (\ref{WahrscheinlichkeitVereinigung}), um die Wahrscheinlichkeit von zu berechnen.
.
Beispiel
Betrachten wir das Experiment, einen Würfel zu werfen, und die folgenden Ereignisse:
- Dass die gewürfelte Zahl ein Vielfaches von drei ist,
- Dass die gewürfelte Zahl
, 
ist.
Beachte, dass 
. Somit sind die Mengen vereinbar. Außerdem haben wir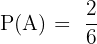 
und 
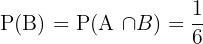. Wir wenden die Formel der Gleichung (\ref{WahrscheinlichkeitVereinigung}) an und erhalten
Wahrscheinlichkeit der Vereinigung unvereinbarer Ereignisse
Wir sagen, dass zwei Ereignisse und unvereinbar sind, wenn sie keine gemeinsamen Elemente haben. Mit anderen Worten: Wenn ein Ergebnis, das in berücksichtigt wird, nicht in enthalten ist und umgekehrt.
Eine andere Möglichkeit besteht darin, dass zwei Ereignisse und unvereinbar sind, wenn ihre Schnittmenge leer ist (es handelt sich um die leere Menge ). Also
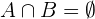
Die Wahrscheinlichkeit der leeren Menge ist 
, da dieses Ereignis kein Ergebnis berücksichtigt. Beachten wir, dass die Gleichung (\ref{ProbabilidadUnion}) sich daher wie folgt vereinfacht:
.
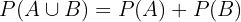
Beispiel
Betrachten wir das Experiment, einen Würfel zu werfen, und die folgenden Ereignisse:
- Dass beim Würfeln die gewürfelte Zahl eine Primzahl kleiner als 4 ist,
- Dass die Zahl
oder die Zahl gewürfelt wird, 
.
Beachten wir, dass 
. Es handelt sich also um unvereinbare Mengen. Außerdem gilt 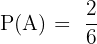und 
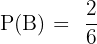. Wir wenden die Formel der Gleichung (\ref{Wahrscheinlichkeitunvereinbar}) an und erhalten
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
