Kapitel

Wahrscheinlichkeitstheorie
In der Wahrscheinlichkeitstheorie geht es darum, jedem möglichen Ergebnis eines Zufallsexperiments eine bestimmte Zahl zuzuordnen, um diese Ergebnisse zu quantifizieren und zu wissen, ob ein Ereignis wahrscheinlicher ist als ein anderes.
Ereignis
Es ist jedes der möglichen Ergebnisse eines Zufallsexperiments.
Beispiel:
- Beim Würfeln ist ein Ergebnis von 5 ein Ereignis
- Beim Werfen von 10 Münzen ist es ein Ereignis, wenn 7 Mal Kopf erscheint
Ergebnisraum
Es handelt sich um die Menge aller möglichen Ergebnisse eines Zufallsexperiments, dargestellt durch  (oder durch den griechischen Buchstaben
(oder durch den griechischen Buchstaben  ).
).
Beispiele:
- Wenn das Ergebnis eines Experiments darin besteht, das Geschlecht eines Neugeborenen zu bestimmen, ist der Ergebnisraum gegeben durch
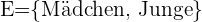
- Wenn bei dem Experiment 2 Münzen nacheinander geworfen werden, dann
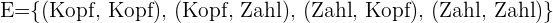
Arten von Ereignissen
Elementarereignis
Ein Elementarereignis ist jedes der Elemente, die Teil des Ergebnisraums sind.
Beispiel:
- Beim Werfen von 3 Münzen, die nacheinander geworfen werden, ist ein Elementarereignis
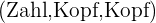
Zusammengesetztes Ereignis
Ein zusammengesetztes Ereignis ist eine beliebige Teilmenge des Ergebnisraums.
Beispiel:
- Wenn beim Werfen von 3 Münzen die erste Münze Kopf zeigt, handelt es sich hierbei um ein zusammengesetztes Ereignis.
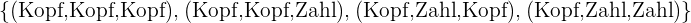
Sicheres Ereignis
Ein sicheres Ereignis  wird durch alle möglichen Ergebnisse (also durch den Ergebnisraum) gebildet.
wird durch alle möglichen Ergebnisse (also durch den Ergebnisraum) gebildet.
Beispiel:
- Dass ein Neugeborenes ein Junge oder ein Mädchen ist, ist ein sicheres Ereignis.
Unmögliches Ereignis
Ein unmögliches Ereignis 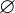 ist dasjenige, das kein Element hat.
ist dasjenige, das kein Element hat.
Beispiel:
- Beim Würfeln eine 7 erhalten.
Vereinbare Ereignisse
Zwei Ereignisse  und
und  , sind vereinbar, wenn sie ein Elementarereignis gemeinsam haben.
, sind vereinbar, wenn sie ein Elementarereignis gemeinsam haben.
Beispiel:
- Aus dem Experiment des Werfens von 2 Münzen geht hervor, dass das Ereignis, bei dem die erste Münze Kopf ist, und das Ereignis, bei dem die zweite Münze Kopf ist, miteinander vereinbar sind, weil
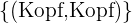 ein gemeinsames Elementarereignis ist
ein gemeinsames Elementarereignis ist
Unvereinbare Ereignisse
Zwei Ereignisse  und
und  sind unvereinbar, wenn sie kein Element gemeinsam haben.
sind unvereinbar, wenn sie kein Element gemeinsam haben.
Beispiel:
- Beim Werfen eines Würfels sind das Ereignis, dass eine 5 und gleichzeitig eine 3 gewürfelt werden, unvereinbare Ereignisse.
Unabhängige Ereignisse
Zwei Ereignisse  und
und  sind unabhängig, wenn die Wahrscheinlichkeit, dass
sind unabhängig, wenn die Wahrscheinlichkeit, dass  eintritt, nicht davon beeinflusst wird, ob
eintritt, nicht davon beeinflusst wird, ob  eingetreten ist oder nicht.
eingetreten ist oder nicht.
Beispiel:
- Beim Werfen von 2 Münzen wird das Ergebnis der zweiten Münze nicht durch das Ergebnis der ersten Münze beeinflusst.
Abhängige Ereignisse
Zwei Ereignisse  und
und  sind abhängig, wenn die Wahrscheinlichkeit, dass
sind abhängig, wenn die Wahrscheinlichkeit, dass  eintritt, davon abhängt, ob
eintritt, davon abhängt, ob  eingetreten ist oder nicht.
eingetreten ist oder nicht.
Beispiel:
- Bei dem Experiment, 2 Münzen zu werfen, kann ein Ereignis A sein, dass die Summe gleich 6 ist, und ein Ereignis B, dass der erste Würfel eine Zahl kleiner oder gleich 5 war. Wenn B nicht eintritt, d. h. wenn eine 6 gewürfelt wurde, ist die Wahrscheinlichkeit, dass A eintritt, geringer, denn die Wahrscheinlichkeit, dass die Summe 6 beträgt, ist gleich 0. Wenn hingegen B eintritt, besteht die Chance, dass die Summe 6 beträgt.
Gegenereignis
Das Gegenereignis zu  ist ein Ereignis, dass eintritt, wenn
ist ein Ereignis, dass eintritt, wenn  nicht ausgeführt wird. Es wird als
nicht ausgeführt wird. Es wird als  notiert.
notiert.
Beispiel:
- Wenn
 das Ereignis ist, bei dem man beim Würfeln eine 2 oder 3 erhält, ist
das Ereignis ist, bei dem man beim Würfeln eine 2 oder 3 erhält, ist  das Ereignis, bei dem man eine andere Zahl als diese erhält,
das Ereignis, bei dem man eine andere Zahl als diese erhält, 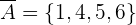
Rechnen mit Ereignissen
Vereinigung von Ereignissen
Die Vereinigung von Ereignissen 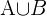 ist das Ereignis, das aus allen Elementen von
ist das Ereignis, das aus allen Elementen von  und
und  besteht.
besteht.
Schnittmenge von Ereignissen
Die Schnittmenge von Ereignissen 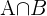 ist das Ereignis, das aus allen Elementen besteht, die sowohl zu
ist das Ereignis, das aus allen Elementen besteht, die sowohl zu  als auch zu
als auch zu  gehören.
gehören.
Differenz von Ereignissen
Die Differenz von Ereignissen 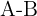 ist das Ereignis, das aus allen Elementen von
ist das Ereignis, das aus allen Elementen von  besteht, die nicht zu
besteht, die nicht zu  gehören.
gehören.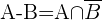
Gegenereignisse
Das Ereignis 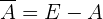 wird Gegenereignis oder komplementäres Ereignis von
wird Gegenereignis oder komplementäres Ereignis von  genannt.
genannt.
Axiome der Wahrscheinlichkeit
1 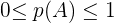 für irgendein Ereignis
für irgendein Ereignis 
2 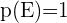 , wobei
, wobei  den Ergebnisraum angibt
den Ergebnisraum angibt
3 Wenn  und
und  nicht vereinbar sind, ist
nicht vereinbar sind, ist 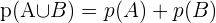
Wahrscheinlichkeitsgesetze
1 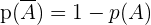
2 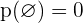
3 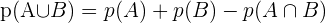
4 Wenn  , ist
, ist 
5 Si 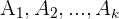 son incompatibles dos a dos entonces:
son incompatibles dos a dos entonces:
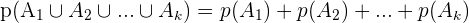
6 Wenn der Ergebnisraum  endlich ist und ein Ereignis
endlich ist und ein Ereignis 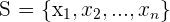 ist, gilt:
ist, gilt:
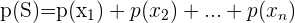
Laplace-Regel
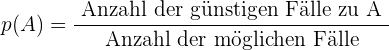
Berechnung der Wahrscheinlichkeiten
Wahrscheinlichkeit der Vereinigung von unvereinbaren Ereignissen
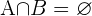

Wahrscheinlichkeit der Vereinigung von vereinbaren Ereignissen
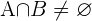
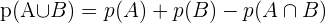
Bedingte Wahrscheinlichkeit
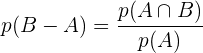
Wahrscheinlichkeit der Schnittmenge von unabhängigen Ereignissen

Wahrscheinlichkeit der Schnittmenge von abhängigen Ereignissen
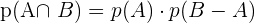
Gesetz der totalen Wahrscheinlichkeit
Wenn 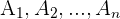 unvereinbare Ereignisse sind, deren Vereinigung der Ergebnisraum
unvereinbare Ereignisse sind, deren Vereinigung der Ergebnisraum  ist und
ist und  ein weiteres Ereignis ist, resultiert daraus:
ein weiteres Ereignis ist, resultiert daraus:

Satz von Bayes
Wenn 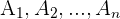 unvereinbare Ereignisse sind, deren Vereinigung der Ergebnisraum
unvereinbare Ereignisse sind, deren Vereinigung der Ergebnisraum  ist und
ist und  ein weiteres Ereignis ist, resultiert daraus:
ein weiteres Ereignis ist, resultiert daraus:
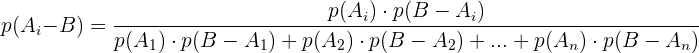
Mit KI zusammenfassen:












