Kapitel
- Wie löst man ein LGS mit zwei Variablen?
- Rechenbeispiel: Lösung eines Gleichungssystems durch das Einsatzverfahren
- Rechenbeispiel: Lösung eines Gleichungssystems durch das Gleichsetzungsverfahren
- Rechenbeispiel: Lösung eines Gleichungssystems durch das Reduktionsverfahren
- Übungsaufgaben zur Lösung von 2x2-Gleichungssystemen
Wie löst man ein LGS mit zwei Variablen?
Um Gleichungssysteme mit zwei Variablen zu lösen, wendet man folgende Rechenverfahren an:
Das Einsatzverfahren
Schritt 1. Löse eine der Gleichungen nach einer der beiden Variablen auf.
Schritt 2. Setze den Ausdruck, den du als Ergebnis erhältst, in die andere Gleichung ein, um eine Gleichung mit nur einer Unbekannten.
Schritt 3. Löse die Gleichung.
Schritt 4. Setze das Ergebnis daraus in die Gleichung ein, in der du nach der ersten Variablen aufgelöst hast.
Schritt 5. Die beiden Werte stellen die Lösungen des Gleichungssystems dar.
Rechenbeispiel: Lösung eines Gleichungssystems durch das Einsatzverfahren
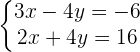
Schritt 1. Löse eine der Gleichungen nach einer der beiden Variablen auf. Wähle dafür die Variable mit dem niedrigsten Koeffizienten.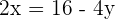 
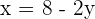
Schritt 2. Ersetze x in der anderen Gleichung mit dem erhaltenen Wert: 
Schritt 3. Löse die Gleichung:
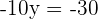
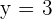
Schritt 4. Setze den Wert in die Gleichung ein, die du durch Auflösen nach der ersten Variablen erhalten hast.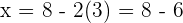
Schritt 5. Lösung: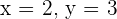
Das Gleichsetzungsverfahren
Schritt 1. Löse beide Gleichungen nach derselben Variable auf.
Schritt 2. Setze die erhaltenen Ausdrücke miteinander gleich, sodass deine Gleichung nur noch eine Unbekannte enthält.
Schritt 3. Löse die Gleichung.
Schritt 4. Setze das Ergebnis in eine der Gleichungen ein, die du zu Beginn nach der Unbekannten aufgelöst hast.
Schritt 5. Die beiden Werte stellen die Lösungen des Gleichungssystems dar.
Rechenbeispiel: Lösung eines Gleichungssystems durch das Gleichsetzungsverfahren
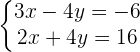
Schritt 1. Löse beide Gleichungen beispielsweise gleichermaßen nach 
auf: 
Schritt 2. Setze beide Ausdrücke miteinander gleich: 
Schritt 3. Löse die Gleichung: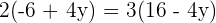
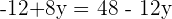
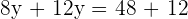
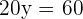
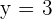
Schritt 4. Setze den Wert von 
in eine der beiden Gleichungen ein, die du durch Auflösen nach erhalten hast:
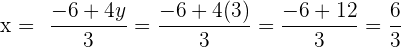
Schritt 5.
Lösung: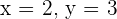
Reduktionsverfahren
Schritt 1. Die beiden Gleichungen werden jeweils mit einem geeigneten Ausdruck multipliziert.
Schritt 2. Bilde die Differenz der beiden Gleichungen, sodass eine der Variablen wegfällt.
Schritt 3. Löse die erhaltene Gleichung.
Schritt 4. Setze das Ergebnis in eine der Ursprungsgleichungen ein und löse diese auf.
Schritt 5. Die beiden Werte stellen die Lösungen des Gleichungssystems dar.
Rechenbeispiel: Lösung eines Gleichungssystems durch das Reduktionsverfahren
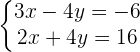
Schritt 1. Es bietet sich an, die Variable y zu eliminieren, um die Gleichungen nicht verändern zu müssen; lass uns hier aber x eliminieren, um das Verfahren besser zu veranschaulichen.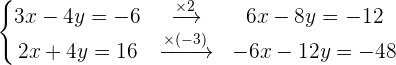 
Schritt 2 und 3. Bilde die Differenz und löse die Gleichung: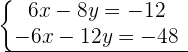 
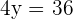
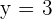
Schritt 4. Setze den Wert von in die zweite Ursprungsgleichung ein:
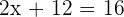
Schritt 5. Lösung: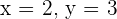
Übungsaufgaben zur Lösung von 2x2-Gleichungssystemen
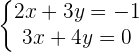
Lösen durch das Einsatzverfahren.
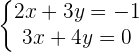
Schritt 1.
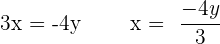
Schritt 2 und 3.
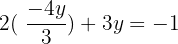
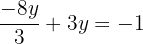
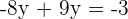
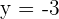
Schritt 4.
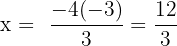
Schritt 5.
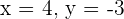
Lösen durch das Gleichsetzungsverfahren.
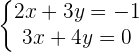
Schritt 1.
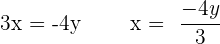
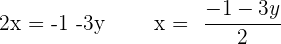
Schritt 2 und 3.
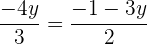
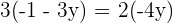
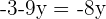
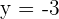
Schritt 4.
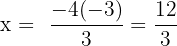
Schritt 5.
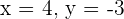
Lösen durch das Reduktionsverfahren.
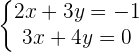Schritt 1.
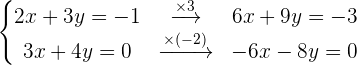Schritt 2 und 3.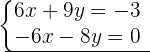
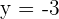
Schritt 4.
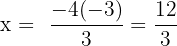
Schritt 5.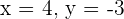
Lösen anhand der grafischen Methode
Stelle beide Gleichungen grafisch im Koordinatensystem dar und du erhältst:
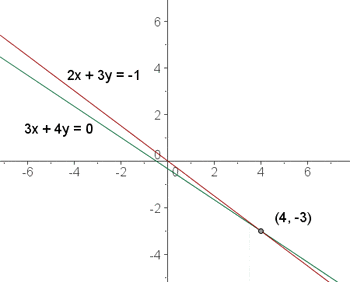
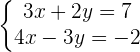
Lösen durch das Einsatzverfahren.
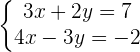
Schritt 1.
Schritt 2 und 3.
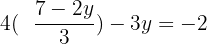
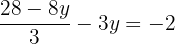
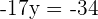
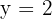
Schritt 4.
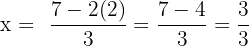
Schritt 5.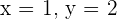
Lösen durch das Gleichsetzungsverfahren.
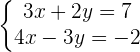
Schritt 1.
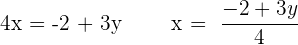
Schritt 2 und 3.
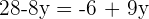
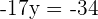
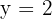
Schritt 4.
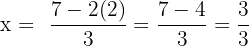
Schritt 5.
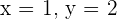
Lösen durch das Reduktionsverfahren.
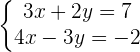
Schritt 1.
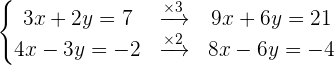
Schritt 2 und 3.
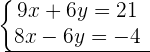
Schritt 4.
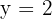
Schritt 5.
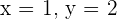
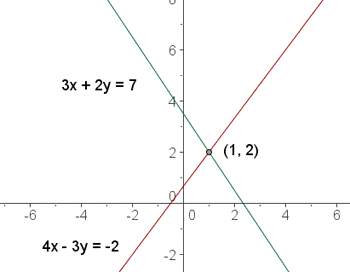
Lösen anhand der grafischen Methode
Stelle beide Gleichungen grafisch im Koordinatensystem dar und du erhältst:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
