Kapitel
Äquivalente Gleichungssysteme sind Gleichungssysteme, die die gleiche Lösung haben, obwohl die Anzahl der Gleichungen unterschiedlich ist. Äquivalente Gleichungssysteme müssen die gleiche Anzahl an Unbekannten haben. Zwei Gleichungen mit zwei Unbekannten bilden zum Beispiel ein System, wenn wir ihre gemeinsame Lösung finden wollen.
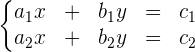
Die Lösung des Systems ist ein Zahlenpaar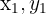 
, so dass, wenn man 
durch 
und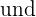 
durch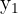 
ersetzt, beide Gleichungen gleichzeitig erfüllt sind.
Wir erhalten äquivalente Systeme durch Eliminierung abhängiger Gleichungen. Wenn:
Alle Koeffizienten sind null.
Zwei Gleichungen sind gleich.
Eine Gleichung ist proportional zur anderen.
Eine Gleichung ist eine lineare Kombination aus anderen Gleichung.
Beispiel für äquivalente Gleichungssysteme
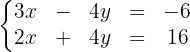
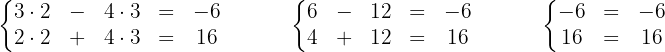
Wie überprüft man, ob ein Gleichungssystem äquivalent ist?
1 Wenn beide Glieder einer Gleichung eines Systems zum selben Ausdruck addiert oder von diesem subtrahiert werden, ist das resultierende System äquivalent.
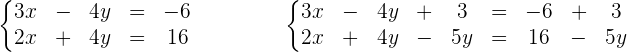
Die Lösungen des Systems sind wie folgt:
2 Multiplizieren oder dividieren wir beide Glieder der Gleichungen eines Systems mit einer Zahl oder durch eine Zahl ungleich null, so ist das resultierende System äquivalent.
Die Lösungen des Systems sind wie folgt:
3 Wenn wir zu einer Gleichung eines Systems eine andere Gleichung desselben Systems addieren oder subtrahieren, ist das resultierende System äquivalent zu dem gegebenen System.
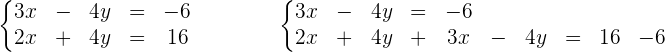
Die Lösungen des Systems sind wie folgt:
4 Ersetzt man eine Gleichung in einem System durch eine andere Gleichung, die sich aus der Addition der beiden Gleichungen des Systems ergibt, die zuvor mit Zahlen ungleich null multipliziert oder dividiert wurden, so ergibt sich ein anderes System, das dem ersten System entspricht.
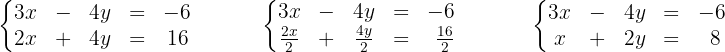
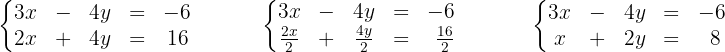
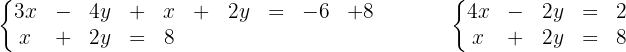
Die Lösungen des Systems sind wie folgt:
5 Wenn man in einem System die Reihenfolge der Gleichungen oder die Reihenfolge der Unbekannten tauscht, resultiert ein anderes äquivalentes System.
Die Lösungen des Systems sind wie folgt:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
