Analysiere das Gleichungssystem und ermittle, für welche Werte von 
das Gleichungssystem lösbar ist. Setze die ermittelten Werte in die Gleichungen ein und löse das Gleichungssystem auf.
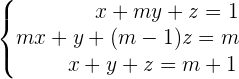
1
Beachte, dass die Reihenfolge der Koeffizienten in jeder Spalte der Reihenfolge ihrer zugehörigen Variablen aus den Gleichungen entsprechen muss. Die Werte in der letzten Spalte, also die konstanten Glieder der Gleichungen, werden mit einem senkrechten Strich vom Rest der Gleichung getrennt dargestellt.
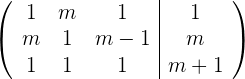
2
Benenne dafür die Zeilen und Spalten mit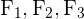 
und 
. Addiere und subtrahiere nun die Zeilen, bis du eine Matrix in Zeilenstufenform erhältst und den Wert von ermittelt hast.
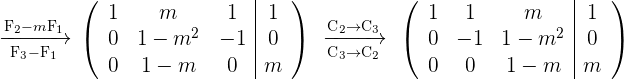
Schreibe die unterste Zeile als Gleichung um:
Hieraus lässt sich schlussfolgern, dass das Gleichungssystem für 
keine Lösungen besitzt, da der Nenner Null wäre. Das Gleichungssystem besitzt folglich Lösungen für 
.
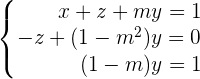
Das Gleichungssystem wird anhand des Werts, den einnimmt, definiert, das heißt:
Analysiere das Gleichungssystem und ermittle, welche Werte annehmen kann, damit das System lösbar ist. Setze dann den bzw. die ermittelten Werte in die Gleichungen ein und löse das Gleichungssystem auf.
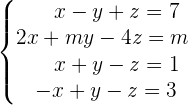
1
Da das Gleichungssystem für die drei Unbekannten mit Koeffizient 1 jeweils unterschiedliche Ergebnisse aufweist, ist das Gleichungssystem nicht lösbar. Dies kann mathematisch bewiesen werden, indem man die erste mit der zweiten Gleichung addiert:
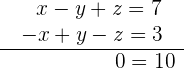
Unabhängig vom Wert besitzt das Gleichungssystem folglich keine gültigen Lösungen.
Analysiere das Gleichungssystem in Abhängigkeit des Werts von 
.
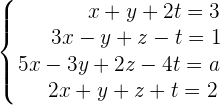
1
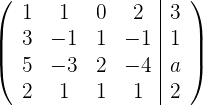
2
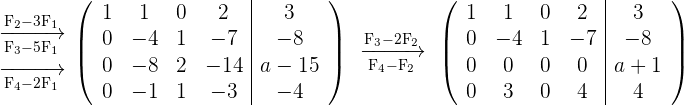
Schreibe die dritte Zeile als Gleichung um:
Hieraus lässt sich schlussfolgern, dass das Gleichungssystem für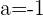 
alle möglichen Lösungen besitzt. Die Werte der Unbekannten sind abhängig vom Wert, der 
zugewiesen wird:
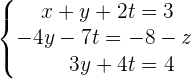
Im Umkehrschluss besitzt das Gleichungssystem für 
keine gültigen Lösungen.
Analysiere für welche Werte von und 
das Gleichungssystem gültige Lösungen besitzt.
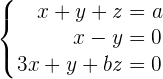
1
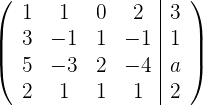
2
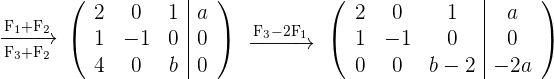
Das Gleichungssystem besitzt für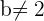 
gültige Lösungen, unabhängig vom Wert, den einnimmt, denn der Koeffizient von ist dann ungleich Null. Die Lösungen sind folglich durch die Werte bestimmt, die und einnehmen:
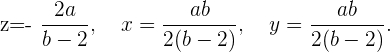
Für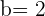 
und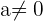 
besitzt das Gleichungssystem keine Lösungen, da 
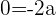wäre.
Im Umkehrschluss besitzt das Gleichungssystem für 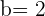und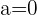 
unendlich viele Lösungen:
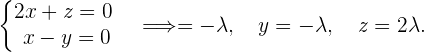
Bestimme für welchen Wert von 
das Gleichungssystem unendlich viele Lösungen besitzt.
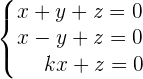
1
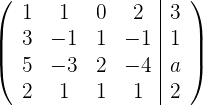
2
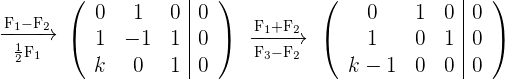
Damit das Gleichungssystem alle möglichen Lösungen besitzt, muss die Matrix eine Reihe aus Nullen enthalten, das heißt das Gleichungssystem besitzt für 
unendlich viele Lösungen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
