Kapitel

Eine Gleichung und ihre Bestandteile
Eine Gleichung ist eine Gleichheit zwischen zwei Ausdrücken, die als Glieder bezeichnet werden und durch das Gleichheitszeichen getrennt sind, wobei es bekannte und unbekannte Elemente gibt. Und diese Gleichheit gilt für bestimmte Werte der Buchstaben.
Beispiel
Die Terme einer Gleichung bilden die Glieder einer Gleichung.
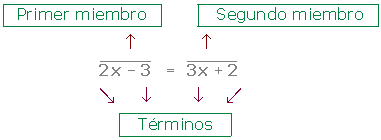
Die Unbekannte einer Gleichung ist der unbekannte Wert, der bestimmt werden soll. Die Unbekannte wird normalerweise durch den Buchstaben  ausgedrückt.
ausgedrückt.
Lösungen
Die Lösungen einer Gleichung sind die Werte, die die Buchstaben annehmen müssen, damit die Gleichung erfüllt ist.
Sieh dir als Beispiel folgende Gleichung an:
die Lösung ist
Wenn wir den Wert von " " durch
" durch  ersetzen, ist die Gleichung erfüllt:
ersetzen, ist die Gleichung erfüllt: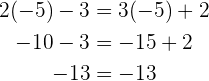
Grad
Der Grad einer Gleichung ist der höchste Exponent, auf den die Unbekannten erhöht werden.
Äquivalente Gleichungen
Zwei Gleichungen sind äquivalent, wenn sie die gleiche Lösung haben.
Zum Beispiel sind die folgenden zwei Gleichungen äquivalent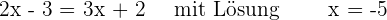
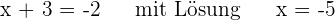
Äquivalenzkriterien für Gleichungen
1 Wenn die beiden Glieder einer Gleichung um den gleichen Betrag addiert oder subtrahiert werden, ist die Gleichung äquivalent zu der gegebenen Gleichung.
Beispiel:
Wir sehen uns folgende Gleichung an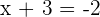
Wir subtrahieren auf beiden Seiten die Zahl 
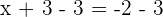
Die neue Gleichung lautet
und ist äquivalent zur ersten Gleichung.
2 Wenn die beiden Glieder einer Gleichung mit der gleichen Zahl multipliziert oder dividiert werden, ist die Gleichung äquivalent zu der gegebenen Gleichung.
Beispiel:
Wir sehen uns folgende Gleichung an: 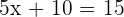
Wir dividieren beide Glieder durch 5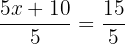
und erhalten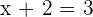
Wenn wir von dieser neuen Gleichung, die der ersten entspricht,  subtrahieren, erhalten wir
subtrahieren, erhalten wir
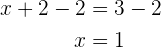
Polynomgleichungen
Polynomgleichungen haben die Form 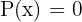 , wobei
, wobei  ein Polynom ist.
ein Polynom ist.
Gleichungen 1. Grades oder lineare Gleichungen
Haben die Form 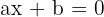 mit
mit 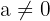 , oder eine beliebige andere Gleichung, die durch Rechenoperationen, das Vertauschen von Termen oder Vereinfachung diesen Ausdruck annehmen.
, oder eine beliebige andere Gleichung, die durch Rechenoperationen, das Vertauschen von Termen oder Vereinfachung diesen Ausdruck annehmen.
Die folgende Gleichung zum Beispiel

Wir berechnen und erhalten
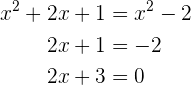
Es handelt sich somit um eine Gleichung 1. Grades.
Gleichungen 2. Grades oder quadratische Gleichungen
Gleichungen der Form  mit
mit 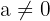 .
.
Es gibt auch unvollständige Gleichungen 2. Grades:
1 
2 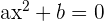
3 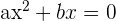
Gleichungen 3. Grades
Gleichungen der Form 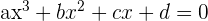 mit
mit 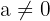 .
.
Gleichungen 4. Grades
Gleichungen der Form  mit
mit 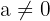 .
.
Biquadratische Gleichungen
Es handelt sich um Gleichungen 4. Grades, die keine Terme ungeraden Grades enthalten. Das heißt,
Gleichungen vom Grad 
Im Allgemeinen haben Gleichungen vom Grad  die Form:
die Form: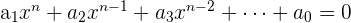
Rationale Polynomgleichungen
Rationale Polynomgleichungen haben die Form 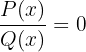 , wobei
, wobei  und
und  Polynome sind.
Polynome sind.
Zum Beispiel:
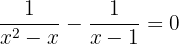
Irrationale Polynomgleichungen
Irrationale Gleichungen sind Gleichungen, die mindestens ein Polynom unter der Wurzel haben.
Sie können wie folgt aussehen:
1 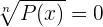
2 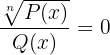
3 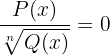
Nicht-polynomische Gleichungen
Exponentialgleichungen
Dies sind Gleichungen, bei denen die Unbekannte im Exponenten steht.
Zum Beispiel
1 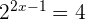
2 
3 
Logarithmusgleichunen
Dies sind Gleichungen, bei denen die Unbekannte durch einen Logarithmus bestimmt wird.
Zum Beispiel
1 
2 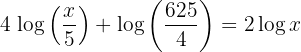
3 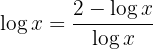
Trigonometrische Gleichungen
Dies sind Gleichungen, bei denen die Unbekannte durch eine trigonometrische Funktion bestimmt wird. Da diese Gleichungen periodisch sind, gibt es normalerweise unendlich viele Lösungen.
Zum Beispiel:
1 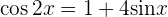
2 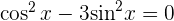
3 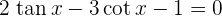
Mit KI zusammenfassen:












