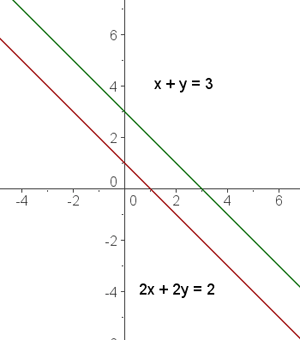Es gibt verschiedene Arten von linearen Gleichungssystemen, die aus zwei Gleichungen und zwei Unbekannten bestehen. Der Grund hierfür ist, dass jede lineare Gleichung mit zwei Variablen als eine Gerade in der Ebene dargestellt werden kann. Bei zwei Gleichungen haben wir also zwei Geraden, die wie folgt auftreten können:
- Zwei Geraden, die sich in einem einzigen Punkt schneiden
- Zwei Geraden, die unendlich viele Punkte gemeinsam haben
- Zwei Geraden, die parallel sind und keinen Punkt gemeinsam haben
Deshalb ist es nötig, Gleichungssysteme zu klassifizieren, da sich für jedes der Systeme eine andere Situation ergibt.
Eindeutig lösbares System
Dieses System hat eine eindeutige Lösung. Das heißt, dass sich die beiden Geraden an einem einzigen Punkt der Ebene schneiden.
Zunächst ermitteln wir die Lösung analytisch und kürzen Variablen. Wir denken daran, dass wir dazu eine Gleichung mit einer angemessenen Zahl multiplizieren müssen, damit eine Variable bei der Addition der Gleichungen wegfällt
Dadurch können wir den anderen Wert bestimmen
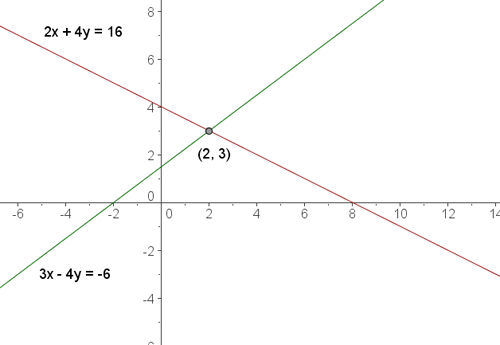
Der Schnittpunkt der beiden Geraden ist
Graphisch dargestellt ist die Lösung der Punkt, an dem sich die zwei Geraden schneiden (Schnittpunkt).
Mehrdeutig lösbares System
Das Hauptmerkmal dieses Systems ist, dass es unendlich viele Lösungen hat. Das heißt, die zwei Geraden liegen aufeinander. Dies bedeutet, dass jeder beliebige Punkt auf der einen Geraden auch ein Punkt auf der anderen Geraden ist. Somit hat das System unendlich viele Lösungen.
Wir betrachten die Lösung analytisch
Wir erkennen, dass die Gleichung immer aufgeht. Dies bedeutet, dass alle beliebigen Punkte 
Lösungen des Systems sind, immer wenn sie sich auf einer Geraden befinden, zum Beispiel 
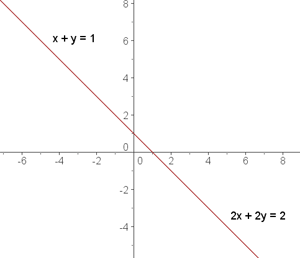
Graphisch dargestellt erhalten wir zwei aufeinanderliegende Geraden. Jeder beliebige Punkt auf der Geraden ist die Lösung.
Unlösbares System
Hier sind beide Geraden Parallelen. Es gibt keine gemeinsamen Punkte. Das System hat somit keine Lösung
Wir betrachten die Lösung analytisch
Wir erhalten 
. Dies ist ein klarer Widerspruch. Das bedeutet, dass es KEINE Punkte in der Ebene gibt, die beide Gleichungen der Geraden gleichzeitig erfüllen.
Graphisch dargestellt erhalten wir zwei parallele Geraden.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
