Löse die folgenden Gleichungssysteme durch Substitution. Wenn eine der Lösungen ein Bruch ist, schreibe sie in der Form 
.
x=
y=
Dieses Feld ist erforderlich.
Wir bestimmen 
in der 2. Gleichung
Wir setzen den Wert von in die 1. Gleichung ein:
Wir setzen den Wert von 
in die 2. Gleichung ein, um zu berechnen:
x=
y=
Dieses Feld ist erforderlich.
Wir entfernen die Klammern:
Wir bestimmen 
in der 2. Gleichung:
Wir setzen den Wert von in die 1. Gleichung ein und bestimmen :
x=
y=
Dieses Feld ist erforderlich.
Wir bestimmen in der 2. Gleichung
Wir setzen den Wert von in die 1. Gleichung ein:
Wir setzen den Wert von in die 2. Gleichung ein, um zu berechnen:
x=
y=
Dieses Feld ist erforderlich.
Wir bestimmen in der 2. Gleichung
Wir setzen den Wert von in die 1. Gleichung ein:
Wir setzen den Wert von in die 2. Gleichung ein, um zu berechnen:
x=
y=
Dieses Feld ist erforderlich.
Wir bestimmen in der 2. Gleichung
Wir setzen den Wert von in die 1. Gleichung ein:
Wir setzen den Wert von in die 2. Gleichung ein, um zu berechnen:
x=
z=
Dieses Feld ist erforderlich.
Wir bestimmen in der 3. Gleichung
Wir setzen den Wert von in die 2. Gleichung ein:
Wir multiplizieren die 1. Gleichung mit 
, setzen den Wert von 
ein und bestimmen den Wert von 
:
Wir ersetzen den Wert von und in der 1. Gleichung und lösen nach 
:
Wir setzen den Wert von durch und , um die Werte von und zu erhalten:
Wir habe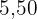n 
€ in 
Münzen zu 
und 
Cent. Wie viele Münzen haben wir von jeder Art?
Münzen zu Cent
Münzen zu Cent
Dieses Feld ist erforderlich.
Wir wandlen zunächst Euro in Cent um:
€ 
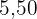Cent.
Wir wählen die Unbekannten:
: Anzahl der Münzen zu 
Cent.: Anzahl der Münzen zu 
Cent.
Wir erstellen die Gleihchungen mit den entsprechenden Werten.
Wir haben 
Münzen und somit 
Der Gesamtwert beträgt 
Cent, somit 
Bevor wir das System lösen, erhalten wir ein äquivalentes System, mit dem wir leichter arbeiten können:
Wir lösen das System:
Wir bestimmen 
in der 1. Gleichung:
Wir setzen in die 2. Gleichung ein und lösen nach 
Wir berechnen den Wert von anhand des Wertes von , indem wir in die 1. Gleichung einsetzen:
Wir haben 
Münzen zu 50 Cent und 
Münzen zu 10 Cent.
Wenn du nicht daran gedacht hast, zu einem einfacheren äquivalenten System zu wechseln, denke daran, dass deine Lösungen die gleichen sind, nur die Berechnungen können ein wenig komplizierter sein. Wir machen es ausnahmsweise:
Wir lösen das System
Wir bestimmen in der 1. Gleichung:
Wir setzen in die 2. Gleichung ein und lösen nach
Wir berechnen den Wert von anhand des Werts von , indem wir in die 1. Gleichung einsetzen:
Wir haben Münzen zu 50 Cent und Münzen zu 10 Cent.
Jonas möchte zuhause eine Party feiern. Er geht zum Supermarkt und kauft 
Packungen Pommes und 
Flaschen Limonade für 
€. Später kauft er noch Packungen Pommes und 
Flasche für 
€. Wieviel kosten die beiden Produkte?
Pommes €
Limonade €
Dieses Feld ist erforderlich.
Wir definieren die Unbekannten:
: Preis für jede Packung Pommes.: Preis für jede Flasche Limonade.
Wir erhalten die Gleichungen mit den entsprechenden Werten.
Für den ersten Einkauf erhalten wir Packungen Pommes und Flaschen für 
€, somit haben wir 
.
Für den zweiten Einkauf erhalten wir Pommes und Flasche für €, somit haben wir 
Wir lösen das System
Wir bestimmen in der 2. Gleichung:
Wir setzen in die 1. Gleichung ein und lösen nach 
Wir berechnen den Wert von anhand des Werts von , indem wir in die 2. Gleichung einsetzen:
Der Preis für eine Packung Pommes ist 
€ und für eine Flasche Limonade 
€.
Zwei Zahlen ergeben 
und das Doppelte einer dieser Zahlen ist 
. Um welche Zahlen handelt es sich (von kleiner nach größer)?
Erste Zahl
Zweite Zahl
Dieses Feld ist erforderlich.
Wir definieren die Unbekannten:
: erste Zahl.: zweite Zahl.
Wir erhalten die Gleichungen mit den entsprechenden Werten.
Die Summe der beiden Zahlen ist 
. Somit haben wir 
.
Das Doppelte einer der Zahlen ist 
. Somit erhalten wir 
Wir lösen das System
Wir bestimmen in der 2. Gleichung:
Wir setzen in die 1. Gleichung ein und lösen nach
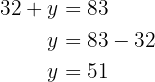
Also sind die gesuchten Zahlen 
und 
.
Ermittle die Maße der Seiten eines Rechtecks, dessen Umfang 48 beträgt und dessen längste Seite dreimal so lang ist wie seine kürzeste Seite.
Längere Seite
Kürzere Seite
Dieses Feld ist erforderlich.
Wir definieren die Unbekannten:
: längere Seite.: kürzere Seite.
Wir erhalten die Gleichungen mit den entsprechenden Werten.
Der Umfang beträgt 
, weshalb wir 
erhalten.
Die längere Seite misst das Dreifache der kleineren Seite, also ergibt sich 
Wir lösen das System
Wir setzen wie folgt ein:
Wir berechnen den Wert von anhand des Werts von , indem wir in die 2. Gleichung einsetzen:
Die längere Seite ist 
und die kleinere Seite ist 
.
Bei einer Prüfung werden richtig beantwortete Fragen mit einem Punkt bewertet und bei falschen Antworten wird ein halber Punkt abgezogen. Insgesamt gibt es 
Fragen und es müssen alle Fragen beantwortet werden. Ein Schüler erzielt 
von Punkten. Berechne die Anzahl der richtig und falsch beantworteten Fragen.
Richtige Antworten
Falsche Antworten
Dieses Feld ist erforderlich.
Wir definieren die Unbekannten:
: richtige Antworten.: falsche Antworten.
Wir erhalten die Gleichungen mit den entsprechenden Werten.
Die Summe der richtigen und falschen Antworten ist . Somit ergibt sich 
.
Die endgültige Punktzahl liegt bei , aber wir haben Fragen. Also müssen wir den im Test erzielten Wert durch Multiplikation mit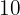 
anpassen. Da richtige Antworten mit Punkt und falsche Antworten mit 
Punkt bewertet werden, ergibt sich 
Wir lösen das System
Wir bestimmen in der 2. Gleichung:
Wir setzen in die 1. Gleichung ein und lösen nach
Wir berechnen den Wert von anhand des Werts von , indem wir in die 2. Gleichung einsetzen:
Die Anzahl der richtigen Antworten ist 
und die Anzahl der falschen Antworten 
.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
