Die Cramersche Regel ist eine effiziente Methode zur Lösung linearer Gleichungssysteme unter Verwendung von Determinanten. Diese Technik ist besonders nützlich bei Systemen von nn Gleichungen mit nn Unbekannten, vorausgesetzt, die Determinante der Koeffizientenmatrix ist ungleich 0.
In diesem Abschnitt stellen wir Übungen vor, die die Anwendung der Cramerschen Regel Schritt für Schritt veranschaulichen. Durch diese Beispiele soll das Verständnis der Methode und ihre Nützlichkeit bei der Lösung von linearen Gleichungssystemen in verschiedenen mathematischen und praxisbezogenen Kontexten gestärkt werden.
Aufgaben
Löse das System mit der Cramerschen Regel
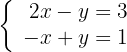
Um das Gleichungssystem mithilfe der Cramerschen Regel zu lösen, müssen wir das Gleichungssystem in Matrizenform ausdrücken. Also folgendes System:
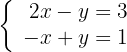
Es kann auch wie folgt geschrieben werden:
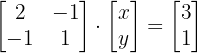
Wir berechnen die Determinante der Matrix:
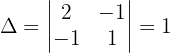
Wir berechnen den Wert von  :
:
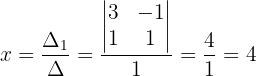
Wir berechnen den Wert von  :
:
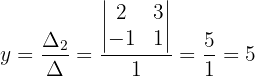
Diskutiere und, wenn möglich, löse das System:
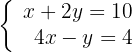
1Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
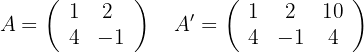
Dann berechnen wir die Ränge der Matrix 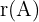 und
und 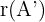 der erweiterten Matrix:
der erweiterten Matrix:
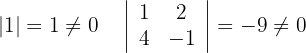
Somit wissen wir, dass 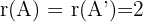 und die Anzahl der Unbekannten
und die Anzahl der Unbekannten 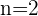 mit
mit 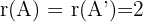 übereinstimmt. Das System isteindeutig lösbar; es hat also eine einzige Lösung.
übereinstimmt. Das System isteindeutig lösbar; es hat also eine einzige Lösung.
2 Wir verwenden die Cramersche Regel, um das System zu lösen:
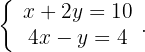
So erhalten wir die folgenden Werte:
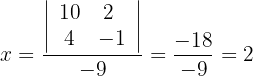
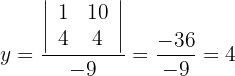
Diskutiere und, wenn möglich, löse das System:
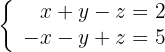
1 Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
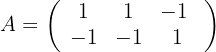
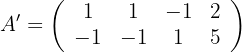
Beachte, dass die Ränge in beiden Fällen 1 sind und folgendes erfüllen:
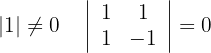
In diesem Fall ist das System nicht lösbar. 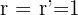 , aber
, aber  r < n[/latex]. Somit gibt es drei Unbekannte und die generierten Ebenen sind parallel. Das System ist also nicht lösbar und hat keine Lösung.
r < n[/latex]. Somit gibt es drei Unbekannte und die generierten Ebenen sind parallel. Das System ist also nicht lösbar und hat keine Lösung.
Löse das homogene System:
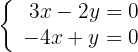
Wir stellen fest, dass die Determinante ungleich 0 ist und der Rang mit der Anzahl der Unbekannten übereinstimmt. Das System hat also eine einzige Lösung.
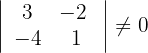
In diesem Fall ist die Lösung die triviale Lösung: 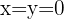
Diskutiere und, wenn möglich, löse das System:
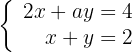
Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
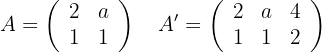
Dann berechnen wir die Determinante der Matrix, um ihren Rang zu bestimmen:

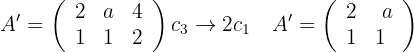
Daraus schließen wir, dass wenn 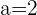 ,
,  und
und 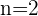 ist . Somit ist das System nicht eindeutig lösbar.
ist . Somit ist das System nicht eindeutig lösbar.
Aus dem Vorherigen können wir schließen, dass wenn 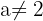 , ist
, ist 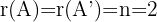 . Somit ist das System nicht eindeutig lösbar.
. Somit ist das System nicht eindeutig lösbar.
Schließlich können wir mithilfe der Cramerschen Regel die Lösung für diesen Fall berechnen:
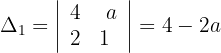
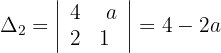
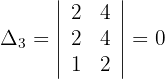
Die Werte der Unbekannten lauten also wie folgt:
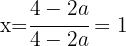

Diskutiere und, wenn möglich, löse das System:
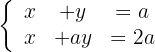
Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
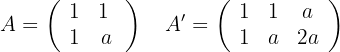
Wir berechnen die Determinanten:
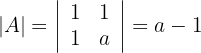
Wenn also 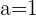 , gilt:
, gilt:
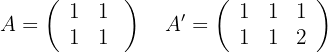
In diesem Fall gilt also 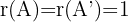 und
und 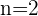 . Wenn also
. Wenn also 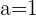 , ist das System nicht lösbar.
, ist das System nicht lösbar.
Löse das System mithilfe der Cramerschen Regel
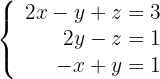
Um das Gleichungssystem mithilfe der Cramerschen Regel zu lösen, müssen wir das Gleichungssystem in Matrizenform ausdrücken. Das heißt, das System:
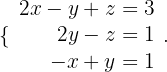
Wir können es auch wie folgt schreiben:
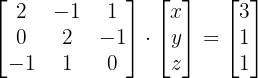
Wir berechnen die Determinante der Matrix:
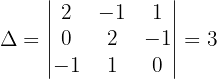
Wir berechnen den Wert von  :
:
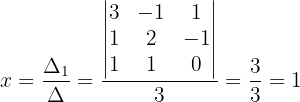
Wir berechnen den Wert von  :
:
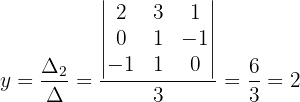
Wir berechnen den Wert von  :
:
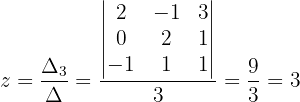
Löse das System mithilfe der Cramerschen Regel
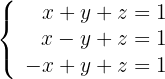
Um das Gleichungssystem mithilfe der Cramerschen Regel zu lösen, müssen wir das Gleichungssystem in Matrizenform ausdrücken. Das heißt, das System:
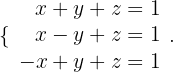
Wir können es auch wie folgt schreiben:

Wir berechnen die Determinante der Matrix:
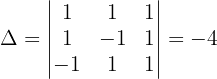
Wir berechnen den Wert von  :
:
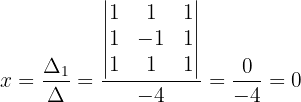
Wir berechnen den Wert von  :
:
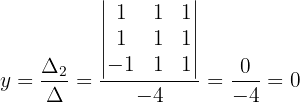
Wir berechnen den Wert von  :
:
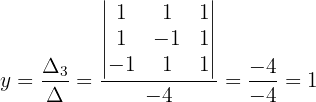
Diskutiere und, wenn möglich, löse das System:
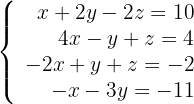
1Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
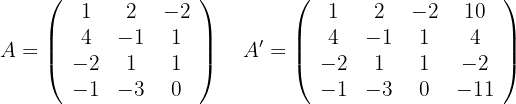
Dann berechnen wir die Ränge der Matrix 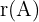 und
und 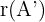 der erweiterten Matrix:
der erweiterten Matrix:
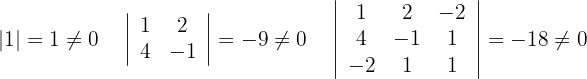
Außerdem gilt:
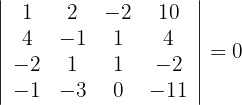
Somit haben wir, dass tenemos que 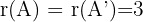 und die Anzahl der Unbekannten
und die Anzahl der Unbekannten 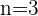 mit
mit 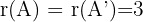 übereinstimmt. Das System ist also eindeutig lösbar; es hat also eine einzige Lösung.
übereinstimmt. Das System ist also eindeutig lösbar; es hat also eine einzige Lösung.
2 Wir reduzieren das System auf ein System mit drei Gleichungen mit drei Unbekannten. Schließlich wenden wir die Cramersche Regel an:
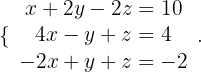
So erhalten wir die folgenden Werte:
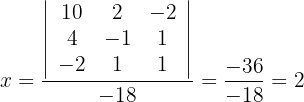
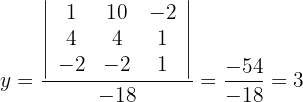
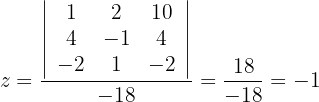
Diskutiere und, wenn möglich, löse das System:
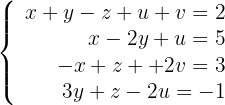
1 Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
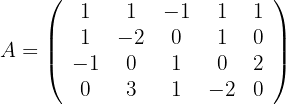
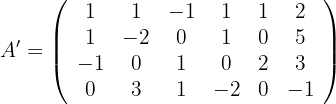
Wir stellen fest, dass die Ränge in beiden Fällen vier sind. Somit gilt:
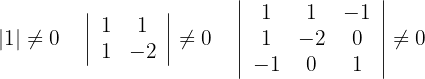
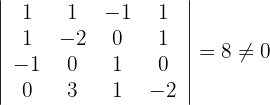
Das System ist in diesem Fall lösbar: 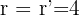 , ist allerdings kleiner als
, ist allerdings kleiner als  und somit gibt es fünf Unbekannte. Das System ist also nicht eindeutig lösbar; das heißt, es hat unendlich viele Lösungen.
und somit gibt es fünf Unbekannte. Das System ist also nicht eindeutig lösbar; das heißt, es hat unendlich viele Lösungen.
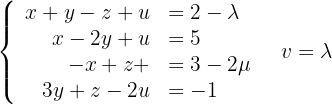
Mithilfe der Cramerschen Regel können wir also die Lösungsmenge berechnen:
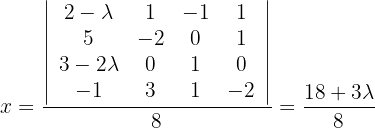
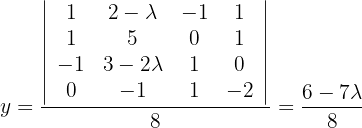
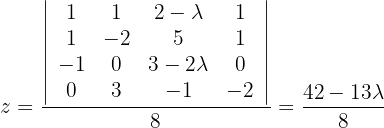
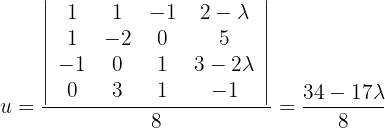
Löse das homogene System:
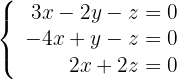
Wir stellen fest, dass die Determinante ungleich 0 ist und der Rang mit der Anzahl der Unbekannten übereinstimmt, so dass die Lösung eindeutig ist.
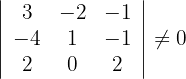
In diesem Fall ist die Lösung die triviale Lösung 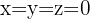
Diskutiere und, wenn möglich, löse das System:
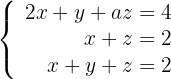
Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
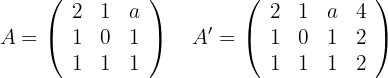
Nun berechnen wir die Determinante der Matrix, um ihren Rang zu bestimmen:
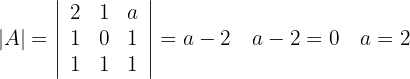
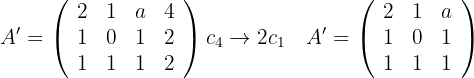
Daraus schließen wir, dass wenn 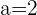 ,
,  und
und 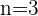 ist. Das System ist also nicht eindeutig lösbar. Nun sehen wir uns einen anderen Fall an:
ist. Das System ist also nicht eindeutig lösbar. Nun sehen wir uns einen anderen Fall an:
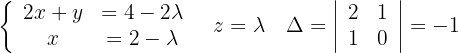
Daraus können wir schließen, dass wenn 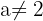 ,
,  ist. Das System ist also eindeutig lösbar.
ist. Das System ist also eindeutig lösbar.
Schließlich wenden wir die Cramersche Regel an und berechnen die Lösung für diesen Fall:
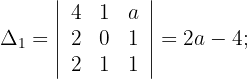
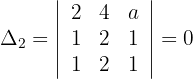

Die Werte der Unbekannten lauten somit:
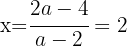


Diskutiere und, wenn möglich, löse das System:
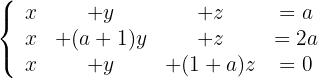
Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
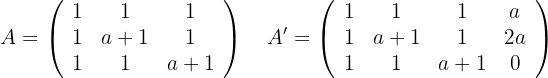
Nun berechnen wir die Determinanten:
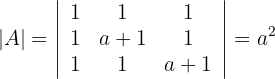
Wenn 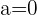 , gilt also:
, gilt also:
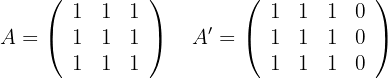
In diesem Fall gilt also 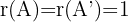 und
und 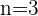 . Wenn
. Wenn 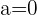 , ist das System nicht eindeutig lösbar. Wir erhalten folgende Lösungsmenge:
, ist das System nicht eindeutig lösbar. Wir erhalten folgende Lösungsmenge:

Andererseits: Wenn 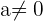 , ist
, ist  . Das System ist nicht eindeutig lösbar. Mithilfe der Cramerschen Regel können wir also die Lösungsmenge berechnen:
. Das System ist nicht eindeutig lösbar. Mithilfe der Cramerschen Regel können wir also die Lösungsmenge berechnen:
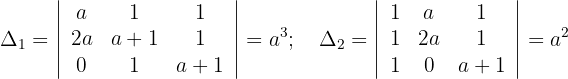
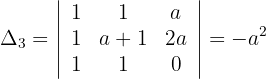
Wir erhalten die folgenden Lösungen:
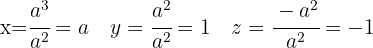
Löse das System, falls es eindeutig lösbar ist.
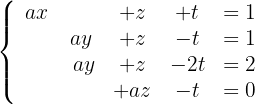
Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
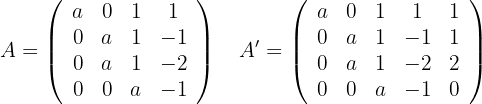
Um die Ränge zu ermitteln, berechnen wir dann die Determinanten:
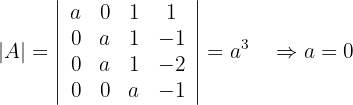
Wenn 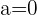 , können wir die Matrizen wie folgt schreiben:
, können wir die Matrizen wie folgt schreiben:
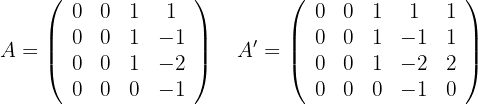
Wir berechnen die Determinanten und erhalten:

Daraus können wir schließen, dass 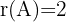 und
und 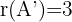 . Wenn
. Wenn 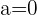 ist das System nicht lösbar.
ist das System nicht lösbar.
Wenn aber 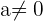 , ist
, ist  . In diesem Fall ist das System eindeutig lösbar.
. In diesem Fall ist das System eindeutig lösbar.
Im Anschluss lösen wir das System für den Fall, dass es resolvemos el sistema para el caso en el que el eindeutig lösbar ist und vereinfachen das System:
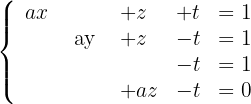
Schließlich berechnen wir die Werte der Unbekannten:
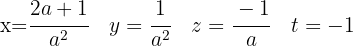
Untersuche das folgende System anhand der unterschiedlichen Werte von  und
und  .
.
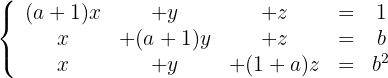
Um herauszufinden, ob das System eindeutig lösbar ist, wenden wir den Satz von Kronecker-Capelli an, so dass die Matrix  (Koeffizientenmatrix) und die erweiterte Matrix
(Koeffizientenmatrix) und die erweiterte Matrix  wie folgt lauten:
wie folgt lauten:
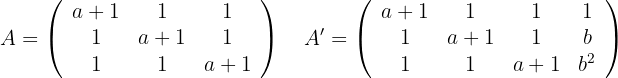
Wir berechnen die Determinante der Matrix  , um die möglichen Werte von
, um die möglichen Werte von  zu ermitteln:
zu ermitteln:
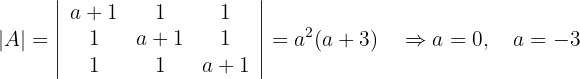
Und so auch wie im ersten Fall: Wenn 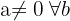 . Es gilt, dass
. Es gilt, dass  . Somit ist das System eindeutig lösbar.
. Somit ist das System eindeutig lösbar.

Wenn  , können wir die Matrizen wie folgt schreiben:
, können wir die Matrizen wie folgt schreiben:
wenn a = 0
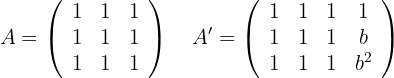
Somit können wir die möglichen Werte von  bestimmen:
bestimmen:
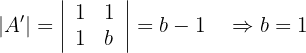
Und so auch wie im zweiten Fall: Wenn  . Es gilt, dass
. Es gilt, dass  , während
, während 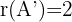 . Das System ist nicht lösbar.
. Das System ist nicht lösbar.
Und wie im dritten Fall: 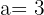 . Es gilt, dass
. Es gilt, dass 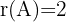 , während
, während 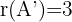 . Das System ist also nicht lösbar.
. Das System ist also nicht lösbar.
Mit KI zusammenfassen:


