Gib an, ob die folgenden Aussagen richtig oder falsch sind:
A Bei einem nicht eindeutig lösbaren System kann eine Gleichung eliminiert werden und man erhält ein äquivalentes System.
B Ein nicht eindeutig lösbares System ist äquivalent zu einem homogenen System.
C Das gesamte nicht eindeutig lösbare System hat zwei gleiche Gleichungen.
D Aus einem lösbaren System können wir ein weiteres unlösbares System extrahieren (nicht äquivalent), indem wir Gleichungen eliminieren.
A Bei einem nicht eindeutig lösbaren System kann eine Gleichung eliminiert werden und man erhält ein äquivalentes System.
Richtig.
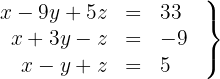
Wir schreiben in Matrizenform

Wir ersetzen die Zeilen  durch
durch 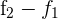 und
und  durch
durch 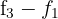 und erhalten so die äquivalente Matrix
und erhalten so die äquivalente Matrix
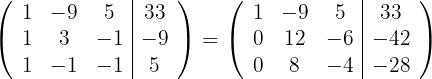
Wir ersetzen die Zeile  durch
durch 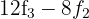 und erhalten durch das 4. Kriterium die äquivalente Matrix
und erhalten durch das 4. Kriterium die äquivalente Matrix
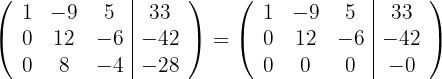
Somit kann die dritte Gleichung eliminiert werden, da sie eine lineare Kombination der beiden anderen Gleichungen ist.
B Ein nicht eindeutig lösbares System ist äquivalent zu einem homogenen System.
Falsch.
Homogene Systeme lassen im Allgemeinen nur die triviale Lösung zu: 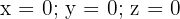 . Eindeutig lösbare Systeme lassen hingegen unendlich viele Lösungen zu.
. Eindeutig lösbare Systeme lassen hingegen unendlich viele Lösungen zu.
C Das gesamte nicht eindeutig lösbare System hat zwei gleiche Gleichungen.
Falsch.
Bei einem lösbaren System sind all seine Gleichungen unterschiedlich
D Aus einem lösbaren System können wir ein weiteres unlösbares System extrahieren (nicht äquivalent), indem wir Gleichungen eliminieren.
Richtig.

Wir schreiben in Matrizenform
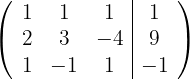
Wir ersetzen die Zeilen  durch
durch 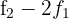 und
und  durch
durch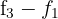 , und erhalten die äquivalente Matrix
, und erhalten die äquivalente Matrix
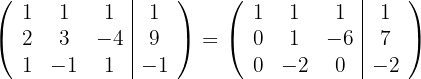
Somit erhalten wir ein eindeutig lösbares System mit der Lösung 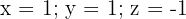
Indem wir die 2. Gleichung des Ausgangssystem eliminieren und 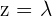 substituieren, erhalten wir das System
substituieren, erhalten wir das System
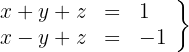
mit der Lösung 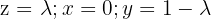
Klassifiziere und löse das folgende Gleichungssystem:
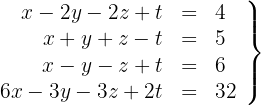
Klassifiziere und löse das folgende Gleichungssystem:
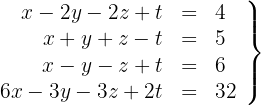
1Wir schreiben in Matrizenform
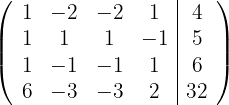
2Wir ersetzen die Zeilen  durch
durch 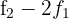 , die Zeile
, die Zeile  durch
durch 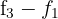 , die Zeile
, die Zeile 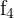 durch
durch 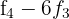 , und erhalten die äquivalente Matrix
, und erhalten die äquivalente Matrix
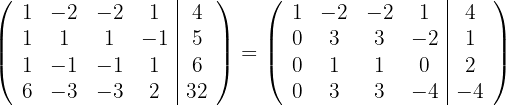
3Wir ersetzen die Zeilen  durch
durch 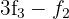 , die Zeile
, die Zeile 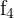 durch
durch 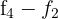 , und erhalten die äquivalente Matrix
, und erhalten die äquivalente Matrix
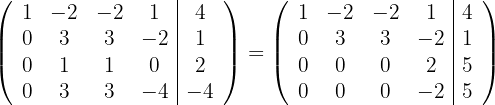
4Wir ersetzen die Zeilen 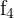 durch
durch  und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
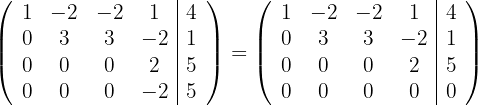
5Das erhaltene System ist nicht eindeutig lösbar. Wir nehmen 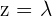 und erhalten die Lösung
und erhalten die Lösung
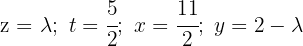
Klassifiziere und löse das folgende Gleichungssystem:
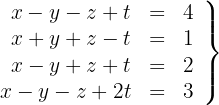
Klassifiziere und löse das folgende Gleichungssystem:
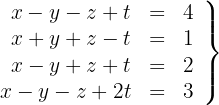
1Wir schreiben in Matrizenform
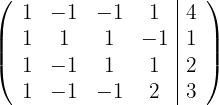
2Wir ersetzen die Zeilen  durch
durch 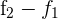 , die Zeile
, die Zeile  durch
durch 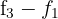 , die Zeile
, die Zeile 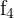 durch
durch 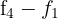 , und erhalten die äquivalente Matrix
, und erhalten die äquivalente Matrix
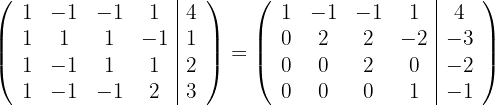
3Das System ist eindeutig lösbar und hat die Lösung
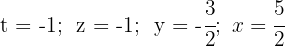
Löse das folgende lineare Gleichungssystem:

Ist es möglich, es in ein nicht eindeutig lösbares System umzuwandeln, indem man nur die dritte Gleichung tauscht?
Löse das folgende lineare Gleichungssystem:

1Wir schreiben in Matrizenform
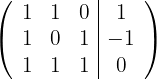
2Wir ersetzen die Zeilen  durch
durch 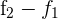 ,
,  durch
durch 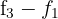 und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
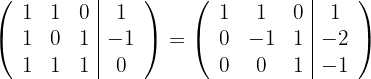
Somit erhalten wir ein eindeutig lösbares System mit der Lösung 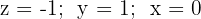
3Ist es möglich, es in ein nicht eindeutig lösbares System umzuwandeln, indem man nur die dritte Gleichung tauscht?
Ja, das ist möglich, indem man einfach die dritte Gleichung zur Summe der ersten und zweiten macht.

Löse das folgende lineare Gleichungssystem:

Ist es möglich, es in ein nicht eindeutig lösbares System umzuwandeln, indem man nur die dritte Gleichung tauscht?
Löse das folgende lineare Gleichungssystem:
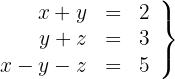
1Wir schreiben in Matrizenform
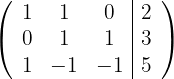
2Wir ersetzen die Zeilen  durch
durch  und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
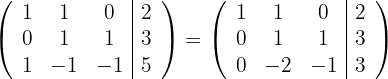
3Wir ersetzen die Zeilen  durch
durch  und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
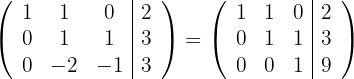
Somit erhalten wir ein eindeutig lösbares System mit der Lösung 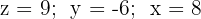
4Ist es möglich, es in ein nicht eindeutig lösbares System umzuwandeln, indem man nur die dritte Gleichung tauscht?
Ja, das ist möglich, indem man einfach die dritte Gleichung zur Summe der ersten und zweiten macht.
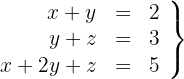
Untersuche, ob es einen Wert von  gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von
gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von  .
.

Untersuche, ob es einen Wert von  gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von
gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von  .
.

1Wir schreiben in Matrizenform
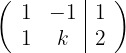
2Wir ersetzen die Zeile  durch
durch 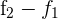 und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
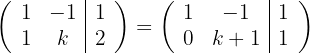
Anhand der Matrix sehen, wir dass, wenn 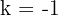 , das System nicht lösbar ist. Wenn
, das System nicht lösbar ist. Wenn  , ist das System eindeutig lösbar.
, ist das System eindeutig lösbar.
Untersuche, ob es einen Wert von  gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von
gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von  .
.
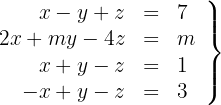
Untersuche, ob es einen Wert von  gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von
gibt, für den das System lösbar ist. Wenn ja, dann löse das System für diesen Wert von  .
.

1Wir schreiben in Matrizenform
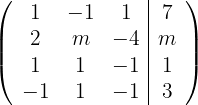
2Wir ersetzen die Zeilen 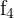 durch
durch  und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
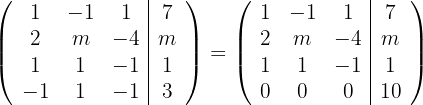
Da 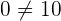 , ist das System für einen beliebigen Wert von
, ist das System für einen beliebigen Wert von  nicht lösbar.
nicht lösbar.
Es gibt drei Barren, die wie folgt zusammengesetzt sind:
- Der erste Barren besteht aus
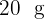 Gold,
Gold,  Silber und
Silber und  Kupfer.
Kupfer. - Der zweite Barren aus
 Gold,
Gold,  Silber und
Silber und 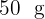 Kupfer.
Kupfer. - Der dritte Barren aus
 Gold,
Gold, 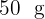 Silber und
Silber und 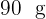 Kupfer.
Kupfer.
Welches Gewicht sollte von jedem der vorherigen Barren genommen werden, um einen neuen Barren mit 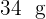 Gold,
Gold, 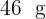 Silber und
Silber und 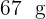 Kupfer.
Kupfer.
Es gibt drei Barren, die wie folgt zusammengesetzt sind:
- Der erste Barren besteht aus
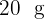 Gold,
Gold,  Silber und
Silber und  Kupfer.
Kupfer. - Der zweite Barren aus
 Gold,
Gold,  Silber und
Silber und 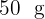 Kupfer.
Kupfer. - Der dritte Barren aus
 Gold,
Gold, 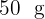 Silber und
Silber und 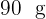 Kupfer.
Kupfer.
Welches Gewicht sollte von jedem der vorherigen Barren genommen werden, um einen neuen Barren mit 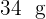 Gold,
Gold, 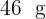 Silber und
Silber und 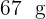 Kupfer herzustellen?
Kupfer herzustellen?
1Wir weisen die Variablen zu
 ist das Gewicht des 1. Barrens.
ist das Gewicht des 1. Barrens.
 ist das Gewicht des 2. Barrens.
ist das Gewicht des 2. Barrens.
 ist das Gewicht des 3. Barrens.
ist das Gewicht des 3. Barrens.
2Wir schreiben die Gleichung für das Gold
Beim 1. Barren gilt für das Gold: 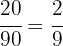
Beim 2. Barren gilt für das Gold: 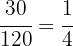
Beim 3. Barren gilt für das Gold: 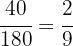
Die Gleichung für das Gold ist:
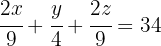
3Wir schreiben die Gleichung für das Silber
Beim 1. Barren gilt für das Silber: 
Beim 2. Barren gilt für das Silber: 
Beim 3. Barren gilt für das Silber: 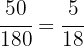
Die Gleichung für das Silber ist:

4Wir schreiben die Gleichung für das Kupfer
Beim 1. Barren gilt für das Kupfer: 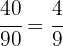
Beim 2. Barren gilt für das Kupfer: 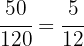
Beim 3. Barren gilt für das Kupfer: 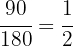
Die Gleichung für das Kupfer ist:
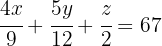
5Wir erhalten das System
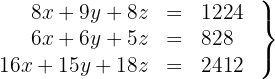
6Wir schreiben in Matrizenform
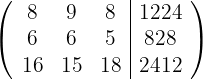
7Wir ersetzen die Zeilen  durch
durch 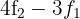 ,
,  durch
durch 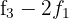 und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
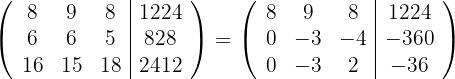
8Wir ersetzen die Zeile  por
por  und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
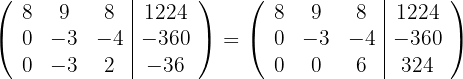
Somit erhalten wir ein eindeutig lösbares System mit der Lösung 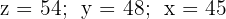
Es gelten dieselben Angaben wie in der vorherigen Aufgabe:
- Der erste Barren besteht aus
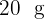 Gold,
Gold,  Silber und
Silber und  Kupfer.
Kupfer. - Der zweite Barren aus
 Gold,
Gold,  Silber und
Silber und 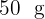 Kupfer.
Kupfer. - Der dritte Barren aus
 Gold,
Gold, 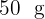 Silber und
Silber und 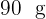 Kupfer.
Kupfer.
Es soll ein Barren mit  Gold,
Gold, 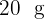 Silber und
Silber und  Kupfer hergestellt werden. Welches Gewicht ist von jedem der Barren zu nehmen?
Kupfer hergestellt werden. Welches Gewicht ist von jedem der Barren zu nehmen?
Es gelten dieselben Angaben wie in der vorherigen Aufgabe:
- Der erste Barren besteht aus
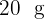 Gold,
Gold,  Silber und
Silber und  Kupfer.
Kupfer. - Der zweite Barren aus
 Gold,
Gold,  Silber und
Silber und 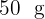 Kupfer.
Kupfer. - Der dritte Barren aus
 Gold,
Gold, 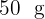 Silber und
Silber und 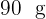 Kupfer.
Kupfer.
Es soll ein Barren mit  Gold,
Gold, 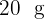 Silber und
Silber und  Kupfer hergestellt werden. Welches Gewicht ist von jedem der Barren zu nehmen?
Kupfer hergestellt werden. Welches Gewicht ist von jedem der Barren zu nehmen?
1Wir weisen die Variablen zu
 ist das Gewicht des 1. Barrens.
ist das Gewicht des 1. Barrens.
 ist das Gewicht des 2. Barrens.
ist das Gewicht des 2. Barrens.
 ist das Gewicht des 3. Barrens.
ist das Gewicht des 3. Barrens.
2Escribimos la ecuación para el oro
Beim 1. Barren gilt für das Gold: 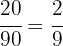
Beim 2. Barren gilt für das Gold: 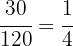
Beim 3. Barren gilt für das Gold: 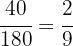
Die Gleichung für das Gold ist:
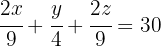
3Wir schreiben die Gleichung für das Silber
Beim 1. Barren gilt für das Silber: 
Beim 2. Barren gilt für das Silber: 
Beim 3. Barren gilt für das Silber: 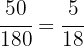
Die Gleichung für das Silber ist:
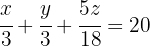
4Wir schreiben die Gleichung für das Kupfer
Beim 1. Barren gilt für das Kupfer: 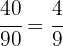
Beim 2. Barren gilt für das Kupfer: 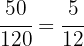
Beim 3. Barren gilt für das Kupfer: 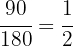
Die Gleichung für das Kupfer ist:
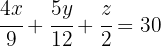
5Wir erhalten das System
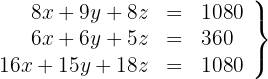
6Wir schreiben in Matrizenform
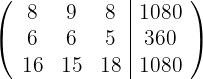
7Wir ersetzen die Zeilen  durch
durch 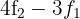 ,
,  durch
durch 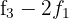 und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
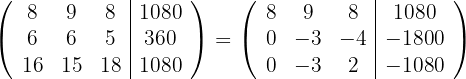
8Wir ersetzen die Zeile  durch
durch  und erhalten die äquivalente Matrix
und erhalten die äquivalente Matrix
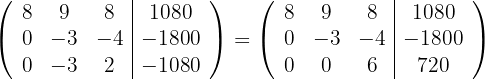
Somit erhalten wir ein eindeutig lösbares System mit der Lösung 
Wie du siehst, hat das System zwar eine Lösung, aber das negative Ergebnis des ersten Barrens zeigt an, dass der Barren mit der geforderten Zusammensetzung nicht hergestellt werden kann, weil die vorhandenen Barren die geforderte Zusammensetzung überschreiten.
Mit KI zusammenfassen:


