Kapitel

Wie mit der Methode der Substitution Gleichungssysteme gelöst werden können
Die Methode der Substitution besteht, wie der Name schon sagt, darin, dass der Wert einer Variablen, der in einer der Gleichungen ermittelt wurde, in die andere Gleichung eingesetzt wird.
Für Gleichungssysteme gilt eine wichtige Regel:
Wenn ein Gleichungssystem mehr Unbekannte (Variablen) hat als Gleichungen, hat das System unendlich viele Lösungen. Das heißt: Da jede Variable verschiedene Werte annehmen kann, so dass sie immer der Gleichung entspricht, ist die Anzahl der Werte, die jede Variable annehmen kann, unendlich.
Gegeben ist die Gleichung: 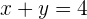
Wir sehen, dass in der Gleichung zwei Variablen vorkommen. Wir können schnell einige der Werte erkennen, die Lösungen sind: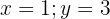
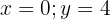
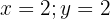
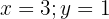

Es gibt eine unendliche Anzahl an Werten, die wir  und
und  zuweisen können, sodass sie Lösungen sind.
zuweisen können, sodass sie Lösungen sind.
Wenn das System andererseits mehr Gleichungen als Unbekannte hat, existiert für das Gleichungssytem eine einzige Lösung.
Beispiele für die Substitution
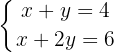
Gleichung I: 
Gleichung II: 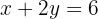
Wir ermitteln in einer der 2 Gleichungen eine der 2 Variablen (wir sollten immer diejenige nehmen, die für unsere Zwecke den geringsten algebraischen Aufwand erfordert), in diesem Fall nehmen wir  in der Gleichung I.
in der Gleichung I.
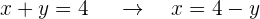
Wir setzen den ermittelten Wert in die andere Gleichung ein, also den Wert für  in die Gleichung II.
in die Gleichung II.

Nun kommt in der Gleichung nur noch die Variable  vor. Diese Gleichung können wir vereinfachen und so den Wert für
vor. Diese Gleichung können wir vereinfachen und so den Wert für  bestimmen.
bestimmen.

Sobald wir den Wert von einer der Variablen ermittelt haben, in diesem Fall  , können wir ihn in eine der 2 Gleichungen einsetzen, um den Wert der anderen Variablen, in diesem Fall
, können wir ihn in eine der 2 Gleichungen einsetzen, um den Wert der anderen Variablen, in diesem Fall  , zu bestimmen.
, zu bestimmen.
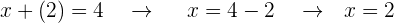
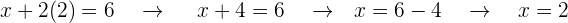
Auf diese Weise erhalten wir den Wert unserer Variablen in einem Gleichungssystem und stellen fest, dass nur eine EINZIGE Lösung existiert.
Aufgaben mit Lösungen zur Substitution
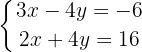
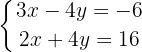 Wir bestimmen
Wir bestimmen  in der zweiten Gleichung und vereinfachen, indem wir durch 2 teilen
in der zweiten Gleichung und vereinfachen, indem wir durch 2 teilen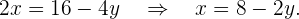
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung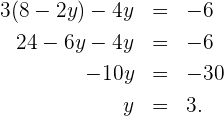
Wir setzen den Wert für  in die zweite Gleichung ein
in die zweite Gleichung ein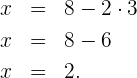
Die Lösung des Gleichungssystems ist also
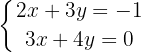
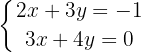
Wir bestimmen  in der zweiten Gleichung
in der zweiten Gleichung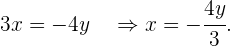
Wir setzen die Variable  in die Gleichung ein
in die Gleichung ein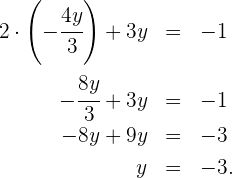
Wir setzen den Wert für  in die zweite Gleichung ein
in die zweite Gleichung ein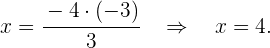
Die Lösung des Gleichungssystems ist also
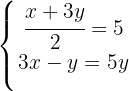
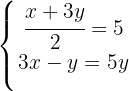
Wir eliminieren die Nenner in der ersten Gleichung, indem wir mit 2 multiplizieren und ordnen die Zweite
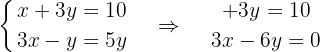
Wir bestimmen  in der zweiten Gleichung
in der zweiten Gleichung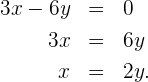
Wir setzen  in die andere Gleichung ein
in die andere Gleichung ein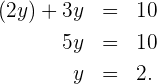
Wir ersetzen den Wert für  durch das ermittelte
durch das ermittelte 
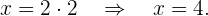
Die Lösung des Gleichungssystems ist also
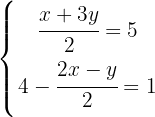
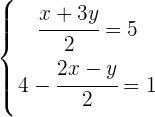
Wir eliminieren die Nenner
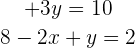
Wir sehen uns die zweite Gleichung an
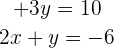
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung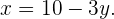
Wir setzen in die zweite Gleichung ein und lösen die Gleichung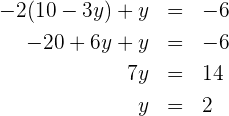
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein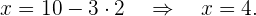
Die Lösung des Gleichungssystem ist also 
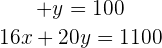
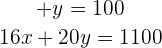
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung 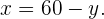
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung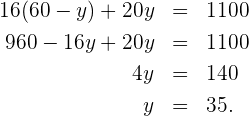
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein
Die Lösung des Gleichungssystems ist also
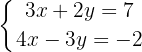
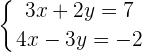
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung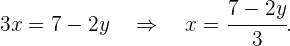
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung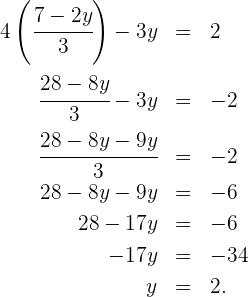
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein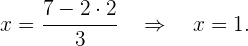
Die Lösung des Gleichungssystems ist also
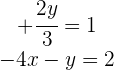
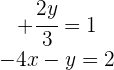
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung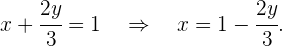
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung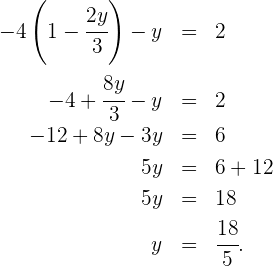
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein
Die Lösung des Gleichungssystems ist also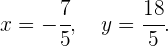
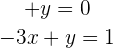
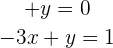
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung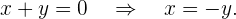
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung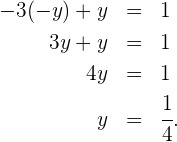
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein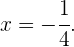
Die Lösung des Gleichungssystems ist also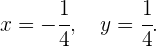
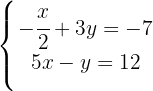
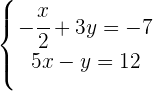
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung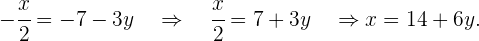
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung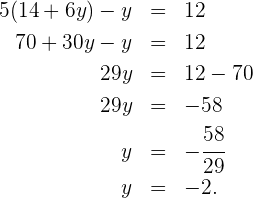
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein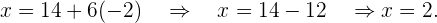
Die Lösung des Gleichungssystems ist also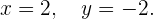
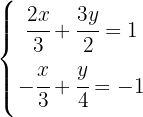
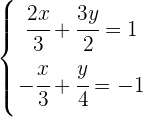
Wir bestimmen  in der ersten Gleichung
in der ersten Gleichung
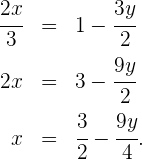
Wir setzen den Wert für  in die andere Gleichung ein und lösen die Gleichung
in die andere Gleichung ein und lösen die Gleichung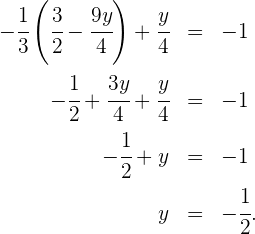
Wir setzen den Wert für  in die erste Gleichung ein
in die erste Gleichung ein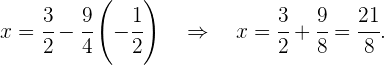
Die Lösung des Gleichungssystems ist also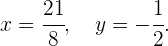
Mit KI zusammenfassen:













