Berechne die geforderten Wahrscheinlichkeiten anhand der folgenden Informationen:
 und
und  sind zwei Zufallsereignisse mit
sind zwei Zufallsereignisse mit
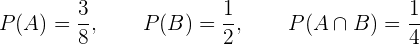
Bestimme:
1 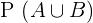
2 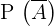
3 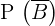
4 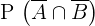
5 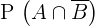
6 
7 
1
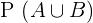
Die Ereignisse sind kompatibel, da die Schnittmenge nicht die leere Menge ist. Das heißt, 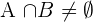 , da die Wahrscheinlichkeit nicht null ist. Somit
, da die Wahrscheinlichkeit nicht null ist. Somit
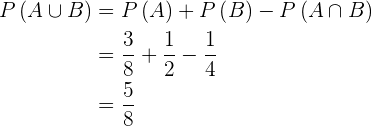
2
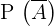
Die Wahrscheinlichkeit von  ist
ist  (totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses
(totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses 
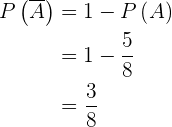
3
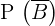
Die Wahrscheinlichkeit von 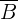 ist
ist  (totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses
(totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses 
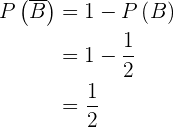
4
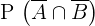
Wir wenden die de-morganschen Gesetze an und erhalten
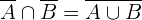
Die Wahrscheinlichkeit von 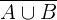 ist außerdem
ist außerdem  (totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses
(totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses 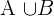 . Somit
. Somit
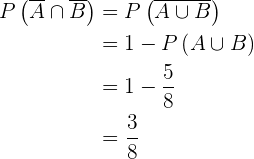
5
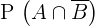
Wir stellen fest:  . Wir wenden das Gesetz an und erhalten
. Wir wenden das Gesetz an und erhalten
6

Wir wenden die de-morganschen Gesetze an und erhalten

Die Wahrscheinlichkeit von  ist
ist  (totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses
(totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses  . Somit
. Somit
7

Wir stellen fest, dass  . Wir erhalten
. Wir erhalten
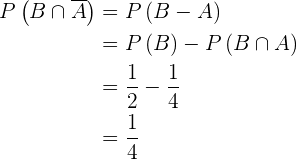
Berechne, was bei den folgenden Ereignissen und deren Wahrscheinlichkeiten verlangt wird.

Bestimme:
1 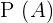
2 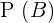
3 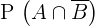
4 
1
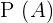
Die Wahrscheinlichkeit von  ist
ist  (totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses
(totale Wahrscheinlichkeit) minus die Wahrscheinlichkeit des Ereignisses 
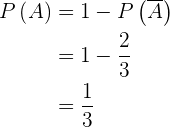
2
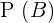
Wir denken daran, dass 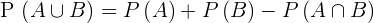 ist. Wenn wir also
ist. Wenn wir also 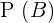 bestimmen, erhalten wir
bestimmen, erhalten wir
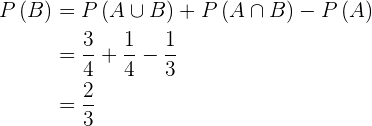
3
Wir stellen fest, dass  . Wir wenden das Gesetz an und erhalten
. Wir wenden das Gesetz an und erhalten
4

Wir stellen fest, dass 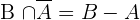 . Wir wenden das Gesetz an und erhalten
. Wir wenden das Gesetz an und erhalten
Beschreibe den Ergebnisraum des folgenden Experiments.
Zwei Kugeln werden aus einer Urne gezogen, in der sich eine weiße, eine rote, eine grüne und eine schwarze Kugel befinden. Beschreibe den Ergebnisraum, wenn:
1 Die erste Kugel wird in die Urne zurückgelegt, bevor die zweite Kugel gezogen wird.
2 Die erste Kugel wird nicht zurückgelegt.
1
Die erste Kugel wird in die Urne zurückgelegt, bevor die zweite Kugel gezogen wird.
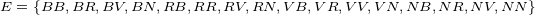
2
Die erste Kugel wird nicht zurückgelegt.
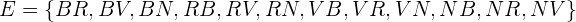
Berechne die Wahrscheinlichkeiten für das folgende Experiment:
In einer Urne befinden sich 8 rote Kugeln, 5 gelbe Kugeln und 5 grüne Kugeln. Eine Kugel wird nach dem Zufallsprinzip gezogen. Berechne folgende Wahrscheinlichkeiten, wenn eine Kugel nach dem Zufallsprinzip gezogen wird:
1 Die Kugel ist rot.
2 Die Kugel ist grün.
3 Die Kugel ist gelb.
4 Die Kugel ist nicht rot.
5 Die Kugel ist nicht gelb.
1
Die Kugel ist rot.
Günstige Fälle:  .
.
Mögliche Ergebnisse: 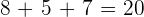 .
.
Die Wahrscheinlichkeit ist somit
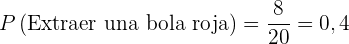
2
Die Kugel ist grün.
Günstige Ergebnisse:  .
.
Mögliche Ergebnisse: 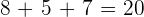 .
.
Die Wahrscheinlichkeit ist somit
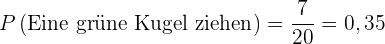
3
Die Kugel ist gelb.
Günstige Ergebnisse:  .
.
Mögliche Ergebnisse: 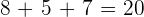 .
.
Die Wahrscheinlichkeit ist somit
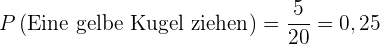
4
Die Kugel ist nicht rot.
Günstige Ergebnisse:  .
.
Mögliche Ergebnisse: 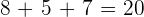 .
.
Die Wahrscheinlichkeit liegt also bei
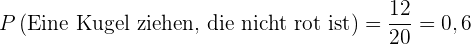
5
Die Kugel ist nicht gelb.
Günstige Ergebnisse:  .
.
Mögliche Ergebnisse: 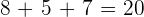 .
.
Die Wahrscheinlichkeit liegt also bei
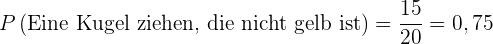
Berechne die Wahrscheinlichkeiten für das folgende Experiment:
In einer Urne sind 3 rote Kugeln und 7 weiße Kugeln. Zwei Kugeln werden nach dem Zufallsprinzip gezogen. Beschreibe den Ergebnisraum und bestimme die Wahrscheinlichkeit der Ereignisse:
1 Mit Austausch (die erste Kugel wird gezogen und vor Ziehung der zweiten Kugel wieder in die Urne gelegt).
2 Ohne Austausch (die erste Kugel wird gezogen und nicht mehr zurückgelegt).
1
Mit Austausch der Kugeln (die erste Kugel wird gezogen und vor Ziehung der zweiten Kugel wieder in die Urne gelegt).
Der Ergebnisraum ist gegeben durch

Die Entnahme von zwei Kugeln mit Austausch sind unabhängige Ereignisse, da die Entnahme der ersten Kugel keine Auswirkung auf die zweite Kugel hat, also
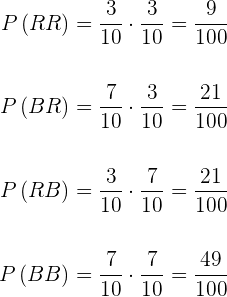
2
Ohne Austausch der Kugeln (die erste Kugel wird gezogen und nicht mehr zurückgelegt).
Der Ergebnisraum ist gegeben durch

Die Entnahme von zwei Kugeln mit Austausch sind abhängige Ereignisse, das sich die Entnahme der ersten Kugel auf die Entnahme der zweiten Kugel auswirkt, also
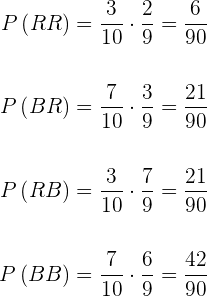
Berechne die Wahrscheinlichkeiten für das folgende Experiment:
Aus einer Urne, in der sich 4 rote Kugeln, 5 weiße Kugeln und 6 schwarze Kugeln befinden, wird eine Kugel gezogen.
1 Wie hoch ist die Wahrscheinlichkeit, dass die Kugel rot oder weiß ist?
2 Wie hoch ist die Wahrscheinlichkeit, dass die Kugel nicht weiß ist?
1
Wie hoch ist die Wahrscheinlichkeit, dass die Kugel rot oder weiß ist?
Die Ziehung von zwei verschiedenfarbigen Kugeln sind inkompatible Ereignisse. Das heißt, ihre Schnittmenge ist die leere Menge. Deshalb
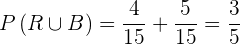
2
Wie hoch ist die Wahrscheinlichkeit, dass die Kugel nicht weiß ist?
Wir denken daran, dass die Wahrscheinlichkeit des Ereignisses 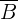
 minus die Wahrscheinlichkeit des Ereignisses
minus die Wahrscheinlichkeit des Ereignisses  ist. Somit
ist. Somit

In einer Klasse sind  Schüler*innen.
Schüler*innen.  Schülerinnen haben blonde Haare,
Schülerinnen haben blonde Haare,  haben dunkle Haare,
haben dunkle Haare,  Schüler sind blond und
Schüler sind blond und  Schüler sind dunkelhaarig. Bestimme die Wahrscheinlichkeit für folgende Fälle:
Schüler sind dunkelhaarig. Bestimme die Wahrscheinlichkeit für folgende Fälle:
1 Es handelt sich um einen Schüler.
2 Es handelt sich um eine Schülerin mit dunklen Haaren.
3 Es handelt sich um einen Schüler oder um eine Schülerin.
1
Es handelt sich um einen Schüler.
Günstige Ergebnisse: 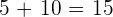 .
.
Mögliche Ergebnisse: 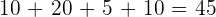 .
.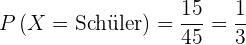
2
Es handelt sich um eine Schülerin mit dunklen Haaren.
Günstige Ergebnisse:  .
.
Mögliche Ergebnisse: 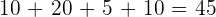 .
.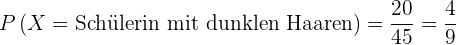
3
Es handelt sich um einen Schüler oder um eine Schülerin.
Günstige Ergebnisse:  .
.
Mögliche Ergebnisse: 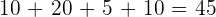 .
.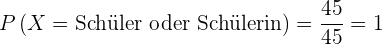
Ein Würfel wird so manipuliert, dass die Wahrscheinlichkeiten, die verschiedenen Seiten zu erhalten, proportional zu den Zahlen auf den Seiten sind.
Bestimme:
1 Die Wahrscheinlichkeit, beim Würfeln eine 6 zu erhalten.
2 Die Wahrscheinlichkeit, beim Würfeln eine ungerade Zahl zu erhalten.
1
Die Wahrscheinlichkeit, beim Würfeln eine 6 zu erhalten.
Wir nennen die Wahrscheinlichkeit  , da sie proportional zu den Zahlen auf den Seiten des Würfels ist:
, da sie proportional zu den Zahlen auf den Seiten des Würfels ist: 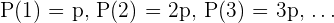 . Für die Summe gilt außerdem, dass
. Für die Summe gilt außerdem, dass
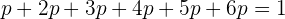
Wir bestimmen  und erhalten
und erhalten
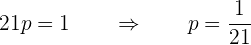
Somit ist 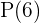
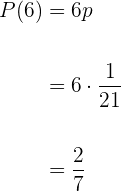
2
Die Wahrscheinlichkeit, beim Würfeln eine ungerade Zahl zu erhalten.
Die ungeraden Zahlen wären  und
und  . Die Wahrscheinlichkeit ist also gegeben durch
. Die Wahrscheinlichkeit ist also gegeben durch
Zwei Würfel werden geworfen und die Summe der erzielten Punkte wird notiert. Bestimme:
1 Die Wahrscheinlichkeit, dass das Ergebnis  ist.
ist.
2 Die Wahrscheinlichkeit, eine gerade Zahl zu erhalten.
3 Die Wahrscheinlichkeit, dass die erhaltene Zahl ein Vielfaches von 3 ist.
1
Die Wahrscheinlichkeit, dass das Ergebnis  ist.
ist.
Günstige Ergebnisse: Die günstigen Ergebnisse sind die  folgenden
folgenden
Mögliche Ergebnisse: Um die möglichen Ergebnisse zu bestimmen, müssen wir die Variationen bei Wiederholung von  Elementen aus
Elementen aus  in
in  berechen:
berechen: .
.
Unsere Wahrscheinlichkeit, dass die Würfel  ergeben, liegt bei
ergeben, liegt bei
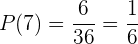 .
.
2
Die Wahrscheinlichkeit, dass das Ergebnis eine gerade Zahl ist
Mögliche Ergebnisse: Aus den vorherigen Angaben wissen wir, dass die möglichen Ergebnisse  sind.
sind.
Günstige Ergebnisse: Die Anzahl der günstigen Ergebnisse, bei denen die Summe gerade ist, ist die Hälfte der möglichen Ergebnisse, da die Summe von zwei geraden Zahlen gerade ist und die Summe von zwei ungeraden Zahlen gerade ist, also sind die günstigen Ergebnisse  .
.
In diesem Fall ist die Wahrscheinlichkeit, dass die Summe gerade ist, gleich
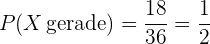 .
.
3
Die Wahrscheinlichkeit, dass die erhaltene Zahl ein Vielfaches von drei ist.
Günstige Ergebnisse: Die günstigen Ergebnisse sind die  folgenden
folgenden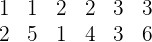
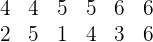
Mögliche Ergebnisse: Aus den vorherigen Angaben wissen wir, dass die möglichen Ergebnisse  sind.
sind.
Die Wahrscheinlichkeit, dass die Summe der Würfel ein Vielfaches von  ergibt, ist also
ergibt, ist also
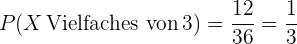 .
.
Es werden 3 Würfel geworfen. Bestimme die Wahrscheinlichkeit für:
1 Alle zeigen eine  .
.
2 Die erzielten Punkte ergeben  .
.
1
Alle Würfel zeigen eine  .
.
Günstige Ergebnisse: Wir haben nur ein günstiges Ergebnis.
Mögliche Ergebnisse: Um die möglichen Ergebnisse zu ermitteln, müssen wir die Variationen bei Wiederholung von  Elementen aus
Elementen aus  in
in  berechnen:
berechnen: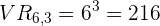 .
.
Die Wahrscheinlichkeit, dass alle Würfel eine  zeigen, liegt bei
zeigen, liegt bei
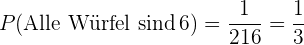 .
.
2
Die erzielten Punkte ergeben  .
.
Günstige Ergebnisse: Die günstigen Ergebnisse sind die  folgenden
folgenden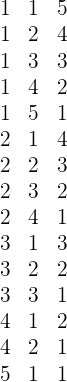
Mögliche Ergebnisse: Aus der vorherigen Angabe wissen wir, dass die möglichen Ergebnisse  sind.
sind.
Somit liegt die Wahrscheinlichkeit, dass die erzielten Punkte  ergeben, bei
ergeben, bei
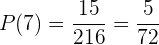 .
.
Ermittle die Wahrscheinlichkeit, dass beim Aufsammeln von Dominosteinen eine Anzahl an Punkten erhalten wird, die größer als  oder ein Vielfaches von
oder ein Vielfaches von  ist.
ist.
Das Domino-Ereignis, bei dem eine Anzahl von Dominosteinen mit einer Punktzahl größer als  erreicht wird, ist gegeben durch
erreicht wird, ist gegeben durch
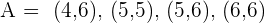
Das Domino-Ereignis, bei dem eine Anzahl von Dominosteinen mit einer Punktzahl, die ein Vielfaches von  ist, erreicht wird, ist gegeben durch
ist, erreicht wird, ist gegeben durch
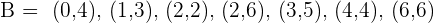
Unser letztes zu berücksichtigendes Ereignis ist also 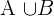 . Außerdem gibt es bei einem Dominospiel
. Außerdem gibt es bei einem Dominospiel  Spielsteine. Die Wahrscheinlichkeit ist also gegeben durch
Spielsteine. Die Wahrscheinlichkeit ist also gegeben durch
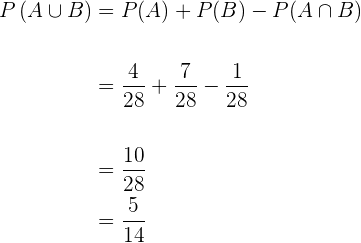
Ermittle die Wahrscheinlichkeit für folgende Ergebnisse beim Werfen eines Würfels:
1 Eine gerade Zahl.
2 Ein Vielfaches von 3.
3 Größer als 4.
1
Eine gerade Zahl.
Günstige Ergebnisse: Die günstigen Ergebnisse sind die  folgenden
folgenden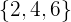
Mögliche Ergebnisse: Da ein Würfel  Seiten hat, haben wir
Seiten hat, haben wir  mögliche Ergebnisse.
mögliche Ergebnisse.
Wie Wahrscheinlichkeit ist somit
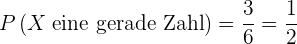 .
.
2
Ein Vielfaches von 3.
Günstige Ergebnisse: Die günstigen Ergebnisse sind die  folgenden
folgenden
Mögliche Ergebnisse: Da ein Würfel  Seiten hat, haben wir
Seiten hat, haben wir  mögliche Ergebnisse.
mögliche Ergebnisse.
Die Wahrscheinlichkeit lautet somit
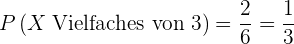 .
.
3
Größer als 4.
Günstige Ergebnisse: Die günstigen Ergebnisse sind die  folgenden
folgenden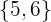
Mögliche Ergebnisse: Da ein Würfel  hat, haben wir
hat, haben wir  mögliche Ergebnisse.
mögliche Ergebnisse.
Die Wahrscheinlichkeit liegt somit bei
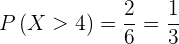 .
.
Bestimme die Wahrscheinlichkeit der Ergebnisse beim Werfen von 2 Münzen:
1 Zweimal Kopf.
2 Zweimal Zahl.
3 Einmal Kopf und einmal Zahl.
1
Zweimal Kopf.
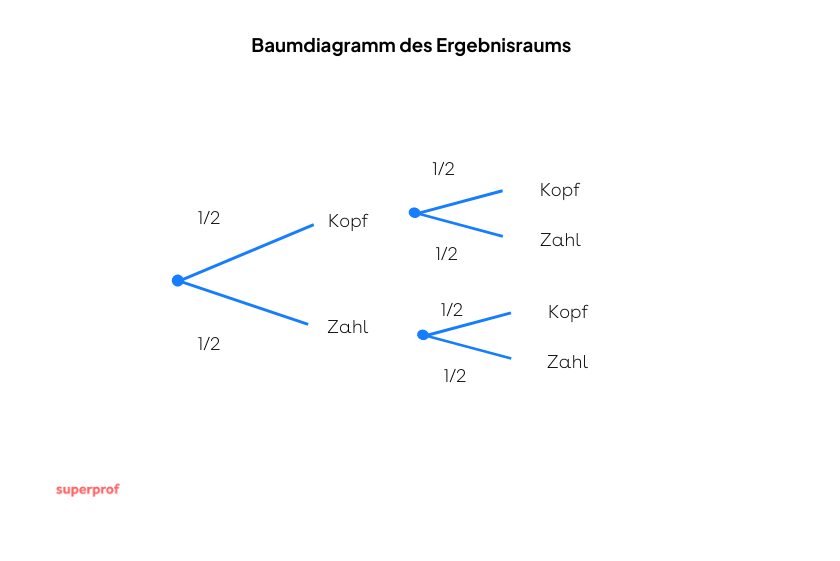
Es handelt sich um unabhängige Ereignisse. Da die Wahrscheinlichkeit, dass jede Münze Kopf ist, 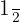 beträgt, ergibt sich Folgendes
beträgt, ergibt sich Folgendes
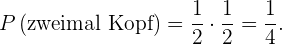
2
Zweimal Zahl.

Wie im vorangegangenen Abschnitt handelt es sich um unabhängige Ereignisse. Da die Wahrscheinlichkeit, dass jede Münze Zahl ist, 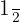 beträgt, ergibt sich Folgendes
beträgt, ergibt sich Folgendes
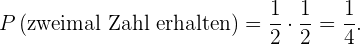
3
Einmal Kopf und einmal Zahl.

Die Wahrscheinlichkeit, dass wir einmal Kopf und einmal Zahl erhalten, ist die Wahrscheinlichkeit, 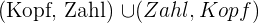 zu erhalten. Außerdem handelt es sich wie in den vorangegangenen Abschnitten um unabhängige Ereignisse. Da die Wahrscheinlichkeit, dass jede Münze Kopf oder Zahl zeigt,
zu erhalten. Außerdem handelt es sich wie in den vorangegangenen Abschnitten um unabhängige Ereignisse. Da die Wahrscheinlichkeit, dass jede Münze Kopf oder Zahl zeigt, 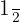 ist, ergibt sich Folgendes
ist, ergibt sich Folgendes
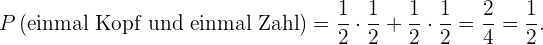
In einem Umschlag befinden sich  Zettel. Auf
Zettel. Auf  davon wurde ein Auto gezeichnet, die restlichen sind weiß. Bestimmte die Wahrscheinlichkeit, dass mindestens ein Zettel mit dem Bild eines Autos darauf gezogen wird:
davon wurde ein Auto gezeichnet, die restlichen sind weiß. Bestimmte die Wahrscheinlichkeit, dass mindestens ein Zettel mit dem Bild eines Autos darauf gezogen wird:
1 Wenn 1 Zettel gezogen wird.
2 Wenn 2 Zettel gezogen werden.
3 Wenn 3 Zettel gezogen werden.
1
Wenn 1 Zettel gezogen wird.
Wir haben günstige Ergebnisse und
günstige Ergebnisse und  mögliche Ergebnisse, deshalb
mögliche Ergebnisse, deshalb
 .
.
2
Es werden 2 Zettel gezogen.
Die Warscheinlichkeit, dass bei der Ziehung von  Zetteln mindestens einer ein Auto zeigt, ist
Zetteln mindestens einer ein Auto zeigt, ist  minus die Wahrscheinlichkeit, dass beim Ziehen von
minus die Wahrscheinlichkeit, dass beim Ziehen von  Zetteln beide weiß sind. Somit
Zetteln beide weiß sind. Somit
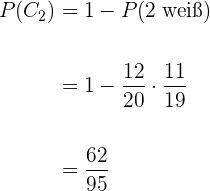
3
Es werden 3 Zettel gezogen.
Die Warscheinlichkeit, dass bei der Ziehung von  Zetteln mindestens einer ein Auto zeigt, ist
Zetteln mindestens einer ein Auto zeigt, ist  minus die Wahrscheinlichkeit, dass beim Ziehen von
minus die Wahrscheinlichkeit, dass beim Ziehen von  Zetteln alle weiß sind. Somit
Zetteln alle weiß sind. Somit
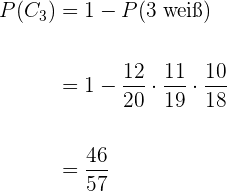
Die Wahrscheinlichkeit, dass die Studenten  und
und  eine Prüfung nicht bestehen, liegt bei jeweils
eine Prüfung nicht bestehen, liegt bei jeweils  und
und  . Die Wahrscheinlichkeit, dass beide die Prüfung nicht bestehen, liegt bei
. Die Wahrscheinlichkeit, dass beide die Prüfung nicht bestehen, liegt bei 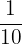 . Bestimme die Wahrscheinlichkeit, dass mindestens einer der beiden Studenten die Prüfung nicht besteht.
. Bestimme die Wahrscheinlichkeit, dass mindestens einer der beiden Studenten die Prüfung nicht besteht.
Wir stellen fest, dass es sich um kompatible Ereignisse handelt, da 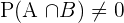 . Somit
. Somit
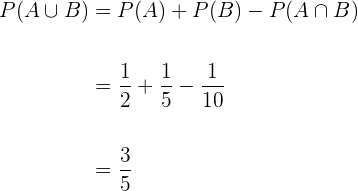
Zwei Brüder gehen auf die Jagd. Der Erste tötet im Schnitt  Tiere pro
Tiere pro  Schüsse. Der Zweite tötet
Schüsse. Der Zweite tötet  Tier pro
Tier pro  Schüsse. Wenn beide auf dasselbe Tier schießen, wie hoch ist die Wahrscheinlichkeit, dass sie es töten?
Schüsse. Wenn beide auf dasselbe Tier schießen, wie hoch ist die Wahrscheinlichkeit, dass sie es töten?
Als Erstes berechnen wir die Wahrscheinlichkeit, dass beide einen Treffer landen. Somit
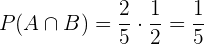
Wir stellen fest, dass die Ereignisse kompatibel sind:
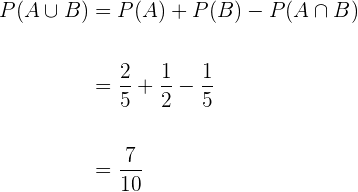
Ein Kurs besteht aus  Männern und
Männern und  Frauen. Die Hälfte der Männer und die Hälfte der Frauen hat braune Augen. Bestimme die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person männlich ist oder braune Augen hat.
Frauen. Die Hälfte der Männer und die Hälfte der Frauen hat braune Augen. Bestimme die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person männlich ist oder braune Augen hat.

Anhand der Tabelle sehen wir, dass die Wahrscheinlichkeit wie folgt lautet
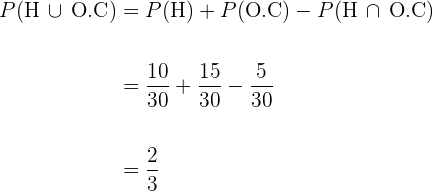
Die Wahrscheinlichkeit, dass ein Mann  Jahre lebt, liegt bei
Jahre lebt, liegt bei  und die Wahrscheinlichkeit, dass seine Frau
und die Wahrscheinlichkeit, dass seine Frau  Jahre lebt, liegt bei
Jahre lebt, liegt bei  . Berechne die Wahrscheinlichkeit:
. Berechne die Wahrscheinlichkeit:
1 Beide leben  Jahre.
Jahre.
2 Der Mann lebt  Jahre, die Frau nicht.
Jahre, die Frau nicht.
3 Beide sterben, bevor die  Jahre vorbei sind.
Jahre vorbei sind.
1
Beide leben  Jahre.
Jahre.
Wir stellen zunächst fest, dass es sich hierbei um unabhängige Ereignisse handelt. Somit
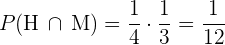
2
Der Mann lebt  Jahre, die Frau nicht.
Jahre, die Frau nicht.
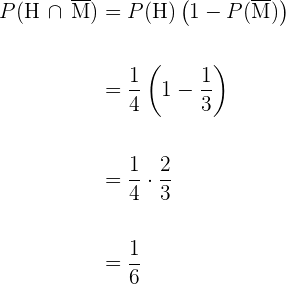
3
Beide sterben, bevor die  Jahre vorbei sind.
Jahre vorbei sind.
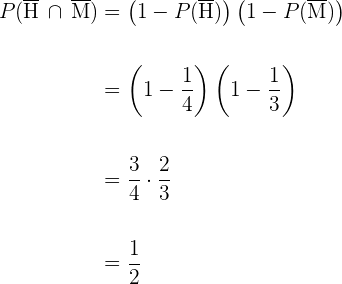
Mit KI zusammenfassen:



