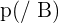und
und  seien zwei Zufallsereignisse mit
seien zwei Zufallsereignisse mit  ,
,  ,
,  .
.
Bestimme:
 Abhängige Ergebnisse
Abhängige Ergebnisse 
 Abhängige Ergebnisse
Abhängige Ergebnisse 
 Kompatible Ergebnisse
Kompatible Ergebnisse 
 Abhängige Ergebnisse
Abhängige Ergebnisse 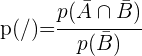
Im Zähler wird das De-morgansche Gesetz angewendet
Im Nenner wenden wir die Wahrscheinlichkeit des Gegenereignisses an
Im Nenner wenden wir die Wahrscheinlichkeit des Gegenereignisses an
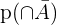
Abhängige Ergebnisse
Im Zähler wird das De-morgansche Gesetz angewendet
Im Nenner wenden wir die Wahrscheinlichkeit des Gegenereignisses an
Im Nenner wenden wir die Wahrscheinlichkeit des Gegenereignisses an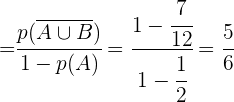
 und
und  seien zwei Zufallsereignisse mit
seien zwei Zufallsereignisse mit  ,
,  ,
,  .
.
Bestimme:

Abhängige Ergebnisse

Abhängige Ergebnisse

Kompatible Ergebnisse

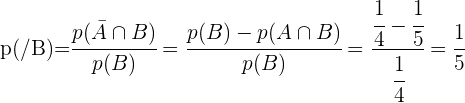

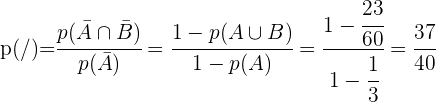

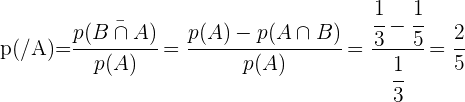
An einer Schule werden als Fremdsprachen Englisch und Französisch zur Auswahl angeboten. In einer Schulklasse wählen  der SchülerInnen Englisch, der Rest Französisch.
der SchülerInnen Englisch, der Rest Französisch. 
der Englischlernenden sind Jungen, ebenso  der Französischlernenden.
der Französischlernenden.
Wie hoch ist die Wahrscheinlichkeit, ein Mädchen auszuwählen, wenn man einen aller SchülerInnen der Klasse nach dem Zufallsprinzip auswählt?
An einer Schule werden als Fremdsprachen Englisch und Französisch zur Auswahl angeboten. In einer Schulklasse wählen  der SchülerInnen Englisch, der Rest Französisch.
der SchülerInnen Englisch, der Rest Französisch.  der Englischlernenden sind Jungen, ebenso
der Englischlernenden sind Jungen, ebenso  der Französischlernenden. Wie hoch ist die Wahrscheinlichkeit, ein Mädchen auszuwählen, wenn man einen aller SchülerInnen der Klasse nach dem Zufallsprinzip auswählt?
der Französischlernenden. Wie hoch ist die Wahrscheinlichkeit, ein Mädchen auszuwählen, wenn man einen aller SchülerInnen der Klasse nach dem Zufallsprinzip auswählt?

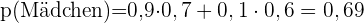
Ein Schüler hat für eine Prüfung nur  der
der  relevanten Themen gelernt. Für die Prüfung werden zwei Themen nach Zufallsprinzip ausgewählt und der Schüler darf eines davon auswählen.
relevanten Themen gelernt. Für die Prüfung werden zwei Themen nach Zufallsprinzip ausgewählt und der Schüler darf eines davon auswählen.
Wie hoch ist die Wahrscheinlichkeit, dass der Schüler ein Thema zur Auswahl bekommt, auf das er gelernt hat?
Ein Schüler hat für eine Prüfung nur  der
der  relevanten Themen gelernt. Für die Prüfung werden zwei Themen nach Zufallsprinzip ausgewählt und der Schüler darf eines davon auswählen.. Wie hoch ist die Wahrscheinlichkeit, dass der Schüler ein Thema zur Auswahl bekommt, auf das er gelernt hat?
relevanten Themen gelernt. Für die Prüfung werden zwei Themen nach Zufallsprinzip ausgewählt und der Schüler darf eines davon auswählen.. Wie hoch ist die Wahrscheinlichkeit, dass der Schüler ein Thema zur Auswahl bekommt, auf das er gelernt hat?
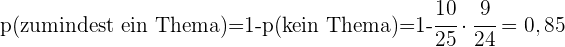
In einer Schulklasse sind  Jungen und
Jungen und  Mädchen;die Hälfte der Mädchen und die Hälfte der Jungen haben Französisch als Wahlfach.
Mädchen;die Hälfte der Mädchen und die Hälfte der Jungen haben Französisch als Wahlfach.
- Wie hoch ist die Wahrscheinlichkeit, dass bei einer zufälligen Auswahl einer Person aus der Klasse ein Junge oder ein/e SchülerIn mit Französisch als Wahlfach ausgewählt wird?
- Wie hoch ist die Wahrscheinlichkeit dass ein Mädchen, das kein Französisch lernt, ausgewählt wird?
In einer Schulklasse sind  Jungen und
Jungen und  Mädchen;die Hälfte der Mädchen und die Hälfte der Jungen haben Französisch als Wahlfach.
Mädchen;die Hälfte der Mädchen und die Hälfte der Jungen haben Französisch als Wahlfach.
a Wie hoch ist die Wahrscheinlichkeit, dass bei einer zufälligen Auswahl einer Person aus der Klasse ein Junge oder ein/e SchülerIn mit Französisch als Wahlfach ausgewählt wird?
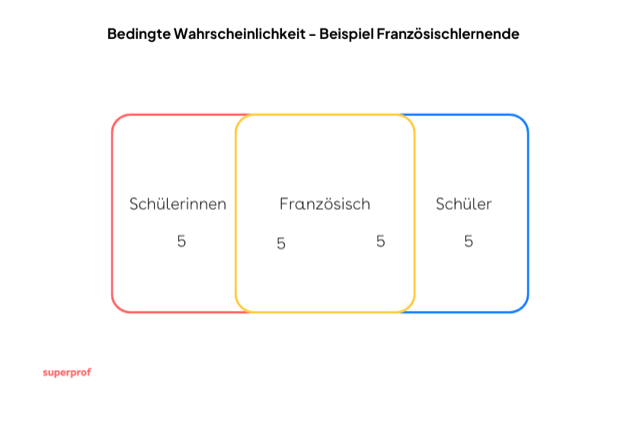
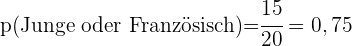
b Wie hoch ist die Wahrscheinlichkeit dass ein Mädchen, das kein Französisch lernt, ausgewählt wird?
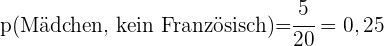
Eine Werkstatt hat ausgerechnet, dass im Durchschnitt morgens drei Personen mit elektrischen Problemen, acht mit mechanischen Problemen und drei mit Karosserieproblemen am Auto kommen. Nachmittags dagegen kommen im Durchschnitt zwei Autos mit elektrischen Problemen, drei mit mechanischen Problemen und eines mit Karosserieproblemen.
a Ordne die zuvor genannten Daten tabellarisch
b Berechne den Prozentsatz der Autos, die nachmittags in der Werkstatt eintreffen
c Berechne den Prozentsatz der Autos, die mit mechanischen Problemen eintreffen
d Berechne die Wahrscheinlichkeit, dass ein Auto mit elektrischen Problemen morgens in der Werkstatt eintrifft
Eine Werkstatt hat ausgerechnet, dass im Durchschnitt morgens drei Personen mit elektrischen Problemen, acht mit mechanischen Problemen und drei mit Karosserieproblemen am Auto kommen. Nachmittags dagegen kommen im Durchschnitt zwei Autos mit elektrischen Problemen, drei mit mechanischen Problemen und eines mit Karosserieproblemen.
- Ordne die zuvor genannten Daten tabellarisch
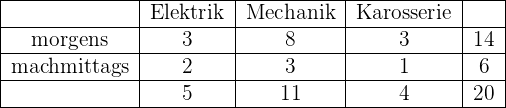
- Berechne den Prozentsatz der Autos, die nachmittags in der Werkstatt eintreffen
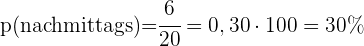
- Berechne den Prozentsatz der Autos, die mit mechanischen Problemen eintreffen
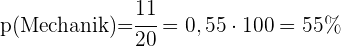
- Berechne die Wahrscheinlichkeit, dass ein Auto mit elektrischen Problemen morgens in der Werkstatt eintrifft
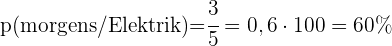
In einer Schulklasse sind  Mädchen und
Mädchen und  Jungen. Ein Komitee aus drei Personen soll gebildet werden. Wie hoch ist die Wahrscheinlichkeit, dass:
Jungen. Ein Komitee aus drei Personen soll gebildet werden. Wie hoch ist die Wahrscheinlichkeit, dass:
- Drei Jungen gewählt werden?
- Genau zwei Jungen und ein Mädchen gewählt werden?
- Mindestens ein Junge gewählt wird?
- Genau zwei Mädchen und ein Junge gewählt werden?
In einer Schulklasse sind  Mädchen und
Mädchen und  Jungen. Ein Komitee aus drei Personen soll gebildet werden. Wie hoch ist die Wahrscheinlichkeit, dass:
Jungen. Ein Komitee aus drei Personen soll gebildet werden. Wie hoch ist die Wahrscheinlichkeit, dass:

a Drei Jungen gewählt werden?
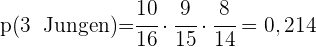
b Genau zwei Jungen und ein Mädchen gewählt werden?
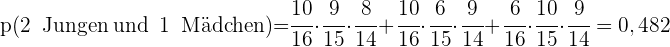
c Mindestens ein Junge gewählt wird?
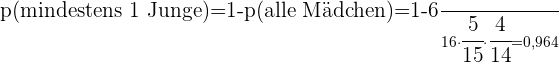
d Genau zwei Mädchen und ein Junge gewählt werden?
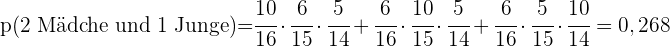
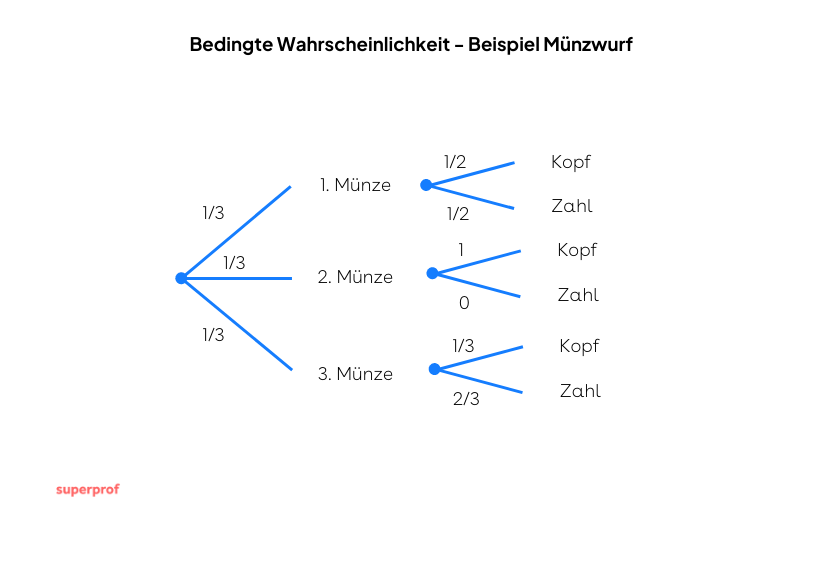
In einer Kiste sind drei Münzen. Eine ist eine gewöhnliche Geldmünze, eine hat zweimal Kopf und eine ist so beschaffen, dass die Wahrscheinlichkeit, Kopf zu erhalten,  beträgt. Eine Münzw wird nach dem Zufallsprinzip ausgewählt und in die Luft geworfen. Wie hoch ist die Wahrscheinlichkeit, Kopf als Ergebnis zu erhalten?
beträgt. Eine Münzw wird nach dem Zufallsprinzip ausgewählt und in die Luft geworfen. Wie hoch ist die Wahrscheinlichkeit, Kopf als Ergebnis zu erhalten?
In einer Kiste sind drei Münzen. Eine ist eine gewöhnliche Geldmünze, eine hat zweimal Kopf und eine ist so beschaffen, dass die Wahrscheinlichkeit, Kopf zu erhalten,  beträgt. Eine Münzw wird nach dem Zufallsprinzip ausgewählt und in die Luft geworfen. Wie hoch ist die Wahrscheinlichkeit, Kopf als Ergebnis zu erhalten?
beträgt. Eine Münzw wird nach dem Zufallsprinzip ausgewählt und in die Luft geworfen. Wie hoch ist die Wahrscheinlichkeit, Kopf als Ergebnis zu erhalten?
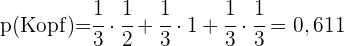
Eine Lostrommel enthält  rote und
rote und  grüne Kugeln. Eine Kugel wird gezogen und durch zwei der anderen Farbe ersetzt. Anschließend wird eine zweite Kugel gezogen. Se pide:
grüne Kugeln. Eine Kugel wird gezogen und durch zwei der anderen Farbe ersetzt. Anschließend wird eine zweite Kugel gezogen. Se pide:
- Wie hoch ist die Wahrscheinlichkeit, dass die zweite Kugel grün ist?
- Wie hoch ist die Wahrscheinlichkeit, dass beide Kugeln die gleiche Farbe aufweisen?
Eine Lostrommel enthält  rote und
rote und  grüne Kugeln. >Eine Kugel wird gezogen und durch zwei der anderen Farbe ersetzt. Anschließend wird eine zweite Kugel gezogen. Se pide:
grüne Kugeln. >Eine Kugel wird gezogen und durch zwei der anderen Farbe ersetzt. Anschließend wird eine zweite Kugel gezogen. Se pide:
a Wie hoch ist die Wahrscheinlichkeit, dass die zweite Kugel grün ist?

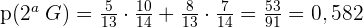
b Wie hoch ist die Wahrscheinlichkeit, dass beide Kugeln die gleiche Farbe aufweisen?
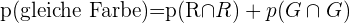
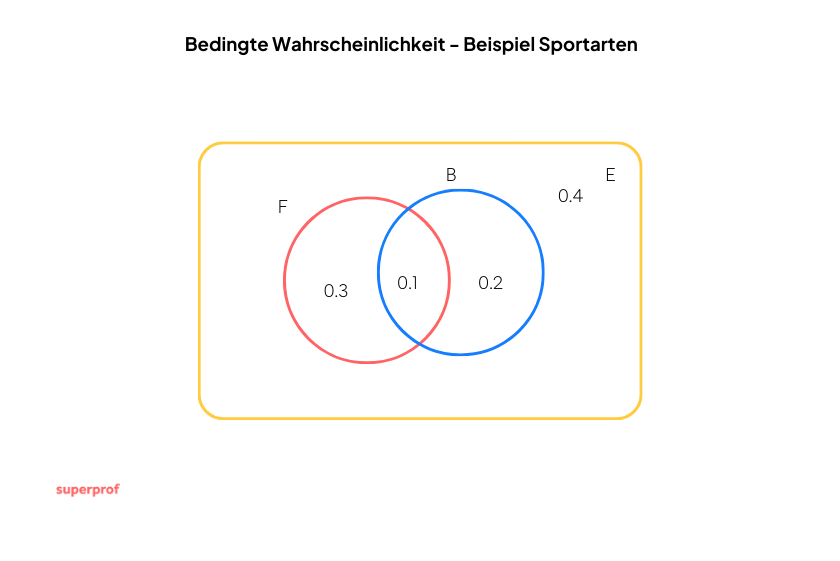
In einer Schulklasse, in der alle SchülerInnen eine Sportart ausüben, spielen  der SchülerInnen Fußball oder Basketball.
der SchülerInnen Fußball oder Basketball.  üben beide Sportarten aus. Wenn außerdem
üben beide Sportarten aus. Wenn außerdem  der SchülerInnen kein Fußball spielen, wie hoch ist die Wahrscheinlichkeit, dass bei Auswahl einer Person aus der Klasse nach dem Zufallsprinzip diese
der SchülerInnen kein Fußball spielen, wie hoch ist die Wahrscheinlichkeit, dass bei Auswahl einer Person aus der Klasse nach dem Zufallsprinzip diese
- nur Fußball spielt?
- nur Basketball spielt?
- eine der Sportarten betreibt?
- weder Fußball noch Basketball spielt?
In einer Schulklasse, in der alle SchülerInnen eine Sportart ausüben, spielen  der SchülerInnen Fußball oder Basketball.
der SchülerInnen Fußball oder Basketball.  üben beide Sportarten aus. Wenn außerdem
üben beide Sportarten aus. Wenn außerdem  der SchülerInnen kein Fußball spielen, wie hoch ist die Wahrscheinlichkeit, dass bei Auswahl einer Person aus der Klasse nach dem Zufallsprinzip diese
der SchülerInnen kein Fußball spielen, wie hoch ist die Wahrscheinlichkeit, dass bei Auswahl einer Person aus der Klasse nach dem Zufallsprinzip diese
a nur Fußball spielt?
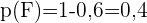

b nur Basketball spielt?

c eine der Sportarten betreibt?

d weder Fußball noch Basketball spielt?

 der Bevölkerung einer Stadt hat braune Haare,
der Bevölkerung einer Stadt hat braune Haare,  braune Augen und
braune Augen und  braune Haare und braune Augen. Eine Person wird nach dem Zufallsprinzip gewählt:
braune Haare und braune Augen. Eine Person wird nach dem Zufallsprinzip gewählt:
- Wenn sie braune Haare hat, wie hoch ist die Wahrscheinlichkeit, dass sie auch braune Augen hat?
- Wenn sie braune Augen hat, wie hoch ist die Wahrscheinlichkeit, dass sie keine braunen Haare hat?
- Wie hoch ist die Wahrscheinlichkeit, dass sie weder braune Haare noch braune Augen hat?
 der Bevölkerung einer Stadt hat braune Haare,
der Bevölkerung einer Stadt hat braune Haare,  braune Augen und
braune Augen und  braune Haare und braune Augen. Eine Person wird nach dem Zufallsprinzip gewählt:
braune Haare und braune Augen. Eine Person wird nach dem Zufallsprinzip gewählt:
a Wenn sie braune Haare hat, wie hoch ist die Wahrscheinlichkeit, dass sie auch braune Augen hat?

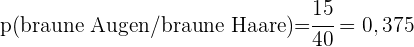
b Wenn sie braune Augen hat, wie hoch ist die Wahrscheinlichkeit, dass sie keine braunen Haare hat?
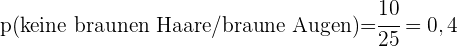
c Wie hoch ist die Wahrscheinlichkeit, dass sie weder braune Haare noch braune Augen hat?
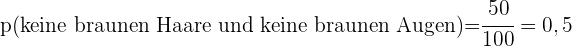
Auf einem Schulhof sind  SchülerInnen, darunter:
SchülerInnen, darunter:  männliche Personen,
männliche Personen,  BrillenträgerInnen und
BrillenträgerInnen und  männliche Brillenträger. Wenn eine Person nach Zufallsprinzip ausgewählt wird:
männliche Brillenträger. Wenn eine Person nach Zufallsprinzip ausgewählt wird:
- Wie hoch ist die Wahrscheinlichkeit, dass sie weiblich ist und keine Brille trägt?
- Wenn wir wissen, dass die ausgewählte Person keine Brille trägt, wie hoch ist die Wahrscheinlichkeit, dass sie männlich ist?
Auf einem Schulhof sind  SchülerInnen, darunter:
SchülerInnen, darunter:  männliche Personen,
männliche Personen,  BrillenträgerInnen und
BrillenträgerInnen und  männliche Brillenträger. Wenn eine Person nach Zufallsprinzip ausgewählt wird:
männliche Brillenträger. Wenn eine Person nach Zufallsprinzip ausgewählt wird:
a Wie hoch ist die Wahrscheinlichkeit, dass sie weiblich ist und keine Brille trägt?
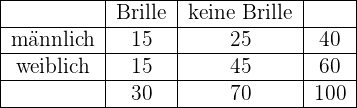
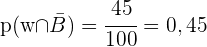
b Wenn wir wissen, dass die ausgewählte Person keine Brille trägt, wie hoch ist die Wahrscheinlichkeit, dass sie männlich ist?
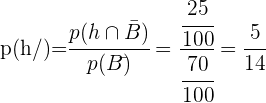
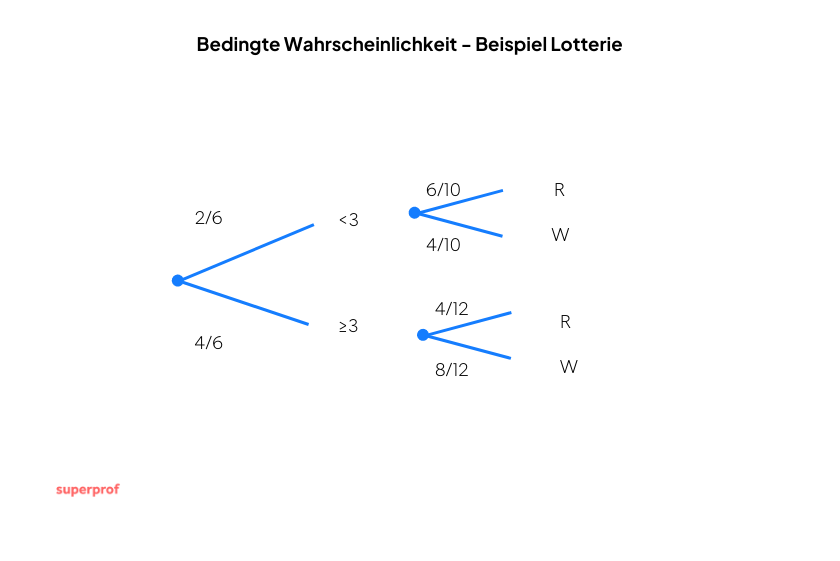
Bei einem Glücksspiel werden zwei Lostrommeln aufgestellt: Trommel  enthält
enthält  rote Kugeln und
rote Kugeln und  weiße Kugeln, Trommel
weiße Kugeln, Trommel  enthält
enthält  rote Kugeln und
rote Kugeln und  weiße Kugeln. Ein Würfel wird geworfen. Wenn eine kleinere Zahl als
weiße Kugeln. Ein Würfel wird geworfen. Wenn eine kleinere Zahl als  gewürfelt wird, wird Trommel
gewürfelt wird, wird Trommel  verwendet; sind die Würfelaugen
verwendet; sind die Würfelaugen  oder mehr, wird Trommel
oder mehr, wird Trommel  verwendet. Anschließend wird aus der entsprechenden Trommel eine Kugel entnommen. Se pide:
verwendet. Anschließend wird aus der entsprechenden Trommel eine Kugel entnommen. Se pide:
- Wie hoch ist die Wahrscheinlichkeit, dass die Kugel rot ist und aus Trommel
 stammt?
stammt? - Wie hoch ist die Wahrscheinlichkeit, dass die Kugel weiß ist?
Bei einem Glücksspiel werden zwei Lostrommeln aufgestellt: Trommel  enthält
enthält  rote Kugeln und
rote Kugeln und  weiße Kugeln, Trommel
weiße Kugeln, Trommel  enthält
enthält  rote Kugeln und
rote Kugeln und  weiße Kugeln. Ein Würfel wird geworfen. Wenn eine kleinere Zahl als
weiße Kugeln. Ein Würfel wird geworfen. Wenn eine kleinere Zahl als  gewürfelt wird, wird Trommel
gewürfelt wird, wird Trommel  verwendet; sind die Würfelaugen
verwendet; sind die Würfelaugen  oder mehr, wird Trommel
oder mehr, wird Trommel  verwendet.
verwendet.
Anschließend wird aus der entsprechenden Trommel eine Kugel entnommen.
a Wie hoch ist die Wahrscheinlichkeit, dass die Kugel rot ist und aus Trommel  stammt?
stammt?
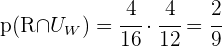
b Wie hoch ist die Wahrscheinlichkeit, dass die Kugel weiß ist?
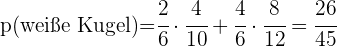
Ein Schüler verwendet vor einer Prüfung einen Wecker, der ihn in  der Fälle verlässlich morgens aufweckt. Wenn er den Wecker hört, beträgt die Wahrscheinlichkeit, dass er an der Prüfung teilnimmt
der Fälle verlässlich morgens aufweckt. Wenn er den Wecker hört, beträgt die Wahrscheinlichkeit, dass er an der Prüfung teilnimmt  . Andernfalls beträgt sie
. Andernfalls beträgt sie  .
.
- Wenn er an der Prüfung teilnimmt, wie hoch ist die Wahrscheinlichkeit, dass er den Wecker gehört hat?
- Wenn er nicht an der Prüfung teilnimmt, wie hoch ist die Wahrscheinlichkeit, dass er den Wecker nicht gehört hat?
Ein Schüler verwendet vor einer Prüfung einen Wecker, der ihn in  der Fälle verlässlich morgens aufweckt. Wenn er den Wecker hört, beträgt die Wahrscheinlichkeit, dass er an der Prüfung teilnimmt
der Fälle verlässlich morgens aufweckt. Wenn er den Wecker hört, beträgt die Wahrscheinlichkeit, dass er an der Prüfung teilnimmt  . Andernfalls beträgt sie
. Andernfalls beträgt sie  .
.
a Wenn er an der Prüfung teilnimmt, wie hoch ist die Wahrscheinlichkeit, dass er den Wecker gehört hat?
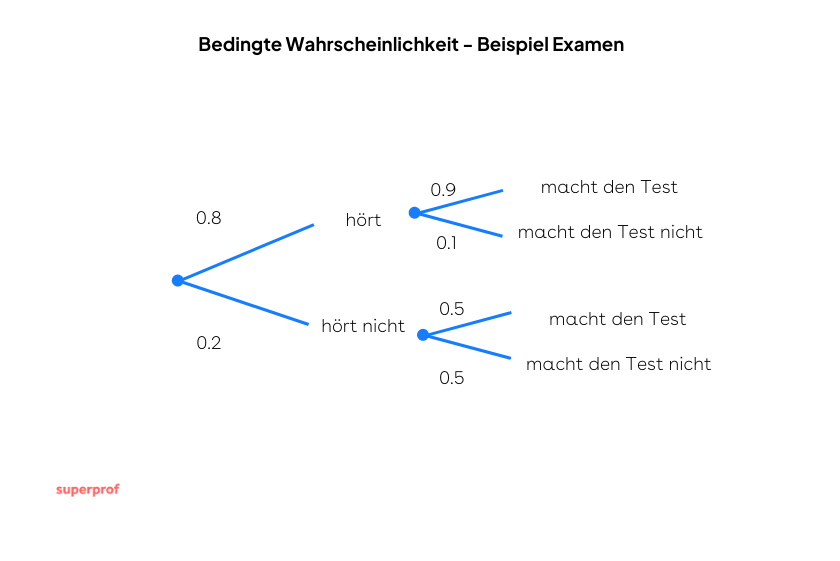
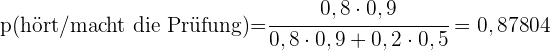
b Wenn er nicht an der Prüfung teilnimmt, wie hoch ist die Wahrscheinlichkeit, dass er den Wecker nicht gehört hat?
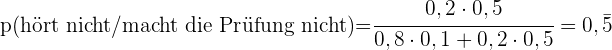
In einem Bücherregal stehen  Romane und
Romane und  Poesiebücher. Eine Person
Poesiebücher. Eine Person  wählt ein Buch aus dem Regal nach Zufallsprinzip aus und nimmt es mit. Danach wählt eine Person
wählt ein Buch aus dem Regal nach Zufallsprinzip aus und nimmt es mit. Danach wählt eine Person  nach Zufallsprinzip ein anderes Buch aus.
nach Zufallsprinzip ein anderes Buch aus.
- Wie hoch ist die Wahrscheinlichkeit, dass Person B einen Roman mitnimmt?
- Wenn man weiß, dass Person B einen Roman mitgenommen hat, wie hoch ist die Wahrscheinlichkeit, dass Person A ein Poesiebuch ausgewählt hat?
In einem Bücherregal stehen  Romane und
Romane und  Poesiebücher. Eine Person
Poesiebücher. Eine Person  wählt ein Buch aus dem Regal nach Zufallsprinzip aus und nimmt es mit. Danach wählt eine Person
wählt ein Buch aus dem Regal nach Zufallsprinzip aus und nimmt es mit. Danach wählt eine Person  nach Zufallsprinzip ein anderes Buch aus.
nach Zufallsprinzip ein anderes Buch aus.
aWie hoch ist die Wahrscheinlichkeit, dass Person B einen Roman mitnimmt?

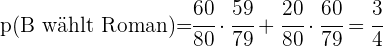
b Wenn man weiß, dass Person B einen Roman mitgenommen hat, wie hoch ist die Wahrscheinlichkeit, dass Person A ein Poesiebuch ausgewählt hat?

Man nehme an, dass  von
von  Männern und
Männern und  von
von  Frauen eine Brille tragen. Wenn die Zahl der Frauen, die an einem Test teilnehmen, viermal so hoch ist wie die der Männer, wie hoch ist die Wahrscheinlichkeit,
Frauen eine Brille tragen. Wenn die Zahl der Frauen, die an einem Test teilnehmen, viermal so hoch ist wie die der Männer, wie hoch ist die Wahrscheinlichkeit,
- eine Person ohne Brille auszuwählen?
- eine Frau mit Brille auszuwählen?
Man nehme an, dass  von
von  Männern und
Männern und  von
von  Frauen eine Brille tragen. Wenn die Zahl der Frauen, die an einem Test teilnehmen, viermal so hoch ist wie die der Männer, wie hoch ist die Wahrscheinlichkeit,
Frauen eine Brille tragen. Wenn die Zahl der Frauen, die an einem Test teilnehmen, viermal so hoch ist wie die der Männer, wie hoch ist die Wahrscheinlichkeit,
a eine Person ohne Brille auszuwählen?
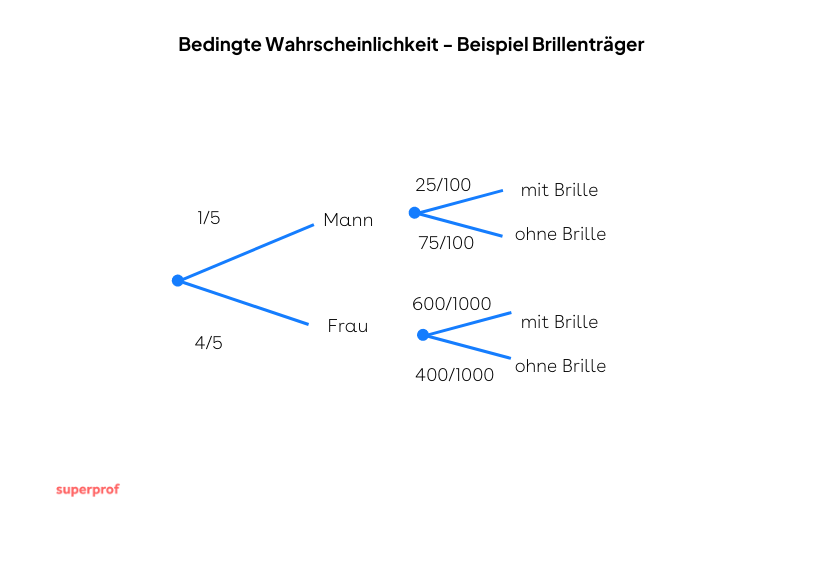
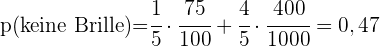
b eine Frau mit Brille auszuwählen?
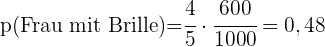
In einem Haus gibt es drei Schlüsselbunde  und
und  ; am ersten hängen 5 Schlüssel, am zweiten 7 und am dritten 8. Nur ein Schlüssel jedes Schlüsselbundes passt in das Schloss zum Geräteschuppen. Ein Schlüsselbund wird nach dem Zufallsprinzip ausgewählt und aus ihm ein Schlüssel, um den Geräteschuppen zu öffnen. Folgendes wird verlangt:
; am ersten hängen 5 Schlüssel, am zweiten 7 und am dritten 8. Nur ein Schlüssel jedes Schlüsselbundes passt in das Schloss zum Geräteschuppen. Ein Schlüsselbund wird nach dem Zufallsprinzip ausgewählt und aus ihm ein Schlüssel, um den Geräteschuppen zu öffnen. Folgendes wird verlangt:
- Wie hoch ist die Wahrscheinlichkeit, dass der richtige Schlüssel gewählt wird?
- Wie hoch ist die Wahrscheinlichkeit, dass der dritte Schlüsselbund gewählt wird und der Schlüssel die Tür nicht öffnet?
- Wenn der gewählte Schlüssel der richtige ist, wie hoch ist die Wahrscheinlichkeit, dass er aus Schlüsselbund
 stammt?
stammt?
In einem Haus gibt es drei Schlüsselbunde  und
und  ; am ersten hängen 5 Schlüssel, am zweiten 7 und am dritten 8. Nur ein Schlüssel jedes Schlüsselbundes passt in das Schloss zum Geräteschuppen. Ein Schlüsselbund wird nach Zufallsprinzip ausgewählt und aus ihm ein Schlüssel, um den Geräteschuppen zu öffnen.
; am ersten hängen 5 Schlüssel, am zweiten 7 und am dritten 8. Nur ein Schlüssel jedes Schlüsselbundes passt in das Schloss zum Geräteschuppen. Ein Schlüsselbund wird nach Zufallsprinzip ausgewählt und aus ihm ein Schlüssel, um den Geräteschuppen zu öffnen.
a Wie hoch ist die Wahrscheinlichkeit, dass der richtige Schlüssel gewählt wird?
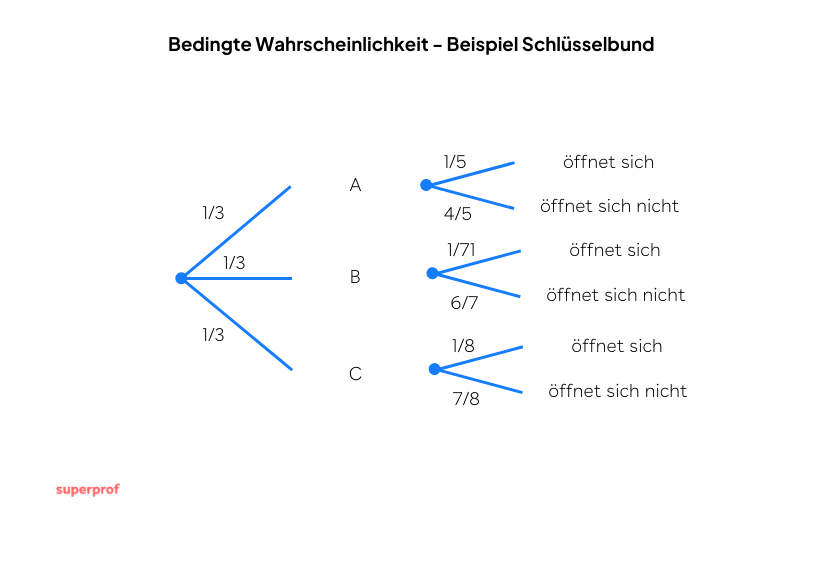
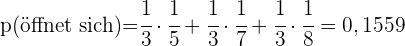
b Wie hoch ist die Wahrscheinlichkeit, dass der dritte Schlüsselbund gewählt wird und der Schlüssel die Tür nicht öffnet? Wenn der gewählte Schlüssel der richtige ist, wie hoch ist die Wahrscheinlichkeit, dass er aus Schlüsselbund  stammt?
stammt?
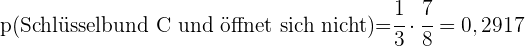
c Wenn der gewählte Schlüssel der richtige ist, wie hoch ist die Wahrscheinlichkeit, dass er aus Schlüsselbund  stammt?
stammt?
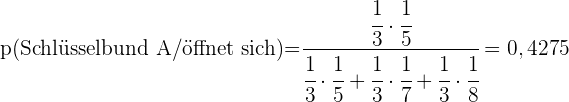
Mit KI zusammenfassen: