Kapitel
Definition des Binomischen Lehrsatzes
Der binomische Lehrsatz ist die Formel, mit der wir die Potenzen eines Binoms ermitteln können.
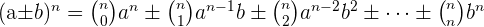
Wir erkennen Folgendes:
Die Anzahl der Terme ist 
.
Die Koeffizienten sind kombinatorische Zahlen, die der n-ten Zeile des Pascalschen Dreiecks entsprechen.
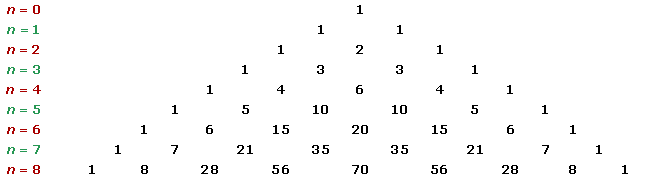
Bei der Entwicklung des Binoms nehmen die Exponenten von 
nach und nach von 
bis Null ab. Die Exponenten von 
nehmen einzeln von Null bis zu, so dass die Summe der Exponenten von und in jedem Term gleich ist.
Wenn einer der Terme des Binoms negativ ist, wechseln sich die positiven und negativen Vorzeichen ab.
Beispiele für den Binomischen Lehrsatz
1 Berechne 
Wir wenden die Formel für den Binomischen Lehrsatz an und erhalten
2 Berechne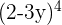 
Wir wenden die Formel für den Binomischen Lehrsatz an und erhalten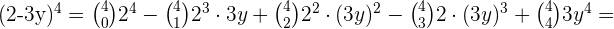
Berechne den Term, der sich an derk-ten Stelle befindet
Mit den folgenden Formeln erhalten wir den Term an der 
-ten Stelle des binomischen Lehrsatzes eines Binoms.
Für das Binom 
gilt, dass sein -ter Term 
ist
Für das Binom 
gilt, dass sein -ter Term 
ist
Beispiele
1 Der fünfte Term der Entwicklung von ist:
Wir wenden die vorhergehende Formel für 
und 
an. Daraus ergibt sich, dass der fünfte Term 
ist
2 Der vierte Term der Entwicklung von 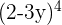ist:
Wir wenden die vorhergehende Formel für 
und 
an. Daraus ergibt sich, dass der vierte Term 
ist
3 Bestimme den achten Term der Entwicklung von 
Wir wenden die vorhergehende Formel für 
und 
. Daraus ergibt sich, dass der achte Term 
ist
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
