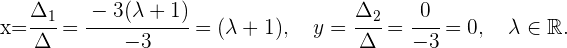Kapitel
Was ist die Cramersche Regel?
In der linearen Algebra ist die Cramersche Regel eine bestimmte Formel, mit der lineare Gleichungssysteme gelöst werden können.
Die Cramersche Regel gilt immer, solange das System eine eindeutige Lösung hat.
Ihr Name geht auf Gabriel Cramer (1704-1752) zurück, der die Formel für eine arbiträre Anzahl an Unbekannten im Jahr 1750 veröffentlichte.
Die Cramersche Regel wird angewandt, um lineare Gleichungssysteme zu lösen, die folgende Bedingungen erfüllen:
1 Die Anzahl der Gleichungen entspricht der Anzahl der Unbekannten.
2 Die Determinante der Koeffizientenmatrix ist ungleich null.
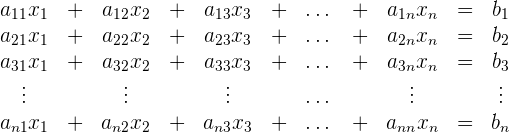
Δ ist die Determinante der Koeffizientenmatrix
Wir denken daran, dass diese Determinante wie folgt berechnet wird
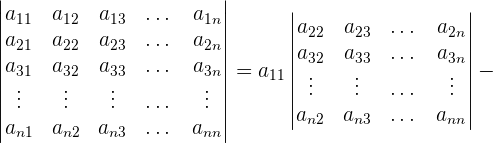
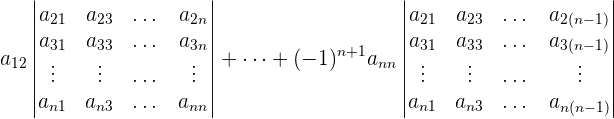
Im Falle von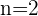 
und 
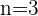lässt sich dies durch einfache Berechnungen ermitteln
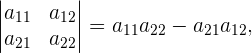
und
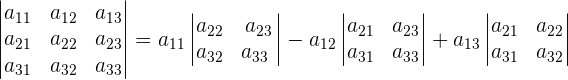
Formel für die Lösung von Cramerschen Systemen
Jedes Cramersche System hat eine eindeutige Lösung, die durch die folgenden Ausdrücke gegeben ist:
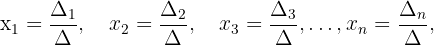
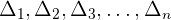sind hierbei die Determinanten, die man erhält, wenn man die Koeffizienten des 2. Glieds (konstante Glieder) in der 1. Spalte, in der 2. Spalte, in der 3. Spalte und der n-ten Spalte jeweils ersetzt.
Aufgaben mit Lösungen für die Cramersche Regel
1
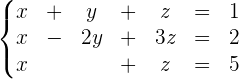
Wir stellen fest, dass die Anzahl der Gleichungen der Anzahl der Unbekannten entspricht und
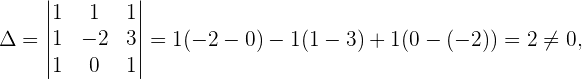
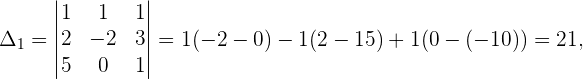
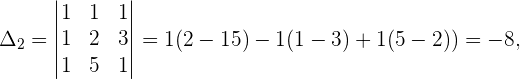
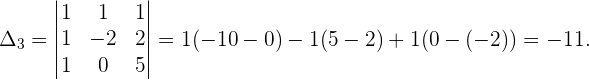
Da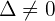 
, sehen wir, dass es sich um ein Cramersches System handelt und es folgende Lösungen gibt
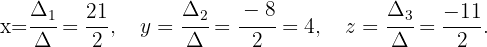
2
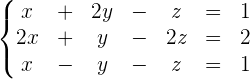
Dieses System hat gleich viele Gleichungen wie Unbekannte, aber die Determinante der Koeffizientenmatrix ist null. Deshalb gilt
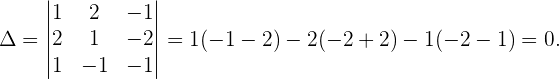
Da es sich nicht um ein Cramersches System handelt, müssen wir es umformen
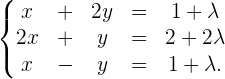
Da die Gleichung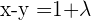 
eine lineare Kombination aus den Gleichungen 
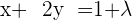und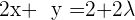 
ist, können wir das System anwenden:
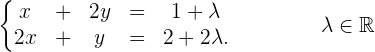
Dies ist ein System mit der gleichen Anzahl an Gleichungen wie Unbekannten und mit einer Determinante der Koeffizientenmatrix ungleich null
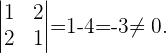
Somit haben wir ein System nach Cramer.
Die Lösungen dieses Systems, die durch die Funktion von λ gegeben sind, sind die gleichen Lösungen wie die des Ausgangssystems.
Wir berechnen zunächst die Determinanten.
Und schließlich setzen wir in die bereits bekannten Formeln ein:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
