Vorgehensweise
Um ein Gleichungssystem mit dem Additions-/Subtraktionsverfahren zu lösen, führen wir folgende Schritte durch:
1 Wir bereiten die beiden Gleichungen vor, indem wir sie mit einer Zahl multiplizieren, sodass die resultierenden Gleichungen einen gemeinsamen Koeffizienten haben
2 Wir subtrahieren (oder addieren; je nach Vorzeichen der Koeffizienten), um eine der Variablen zu eliminieren
3 Wir lösen die resultierende Gleichung
4 Wir setzen den erhaltenen Wert in eine der Ausgangsgleichungen ein und lösen sie
5 Die beiden resultierenden Werte sind die Lösung des Systems
Beispiele für das Additions-/Subtraktionsverfahren
In diesem Fall gibt es zwei Möglichkeiten, das folgende Gleichungssystem zu lösen:
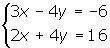
Durch Multiplikation
1 Wir eliminieren die Variable x, indem wir die erste Gleichung mit 2 und die zweite Gleichung mit −3 multiplizieren
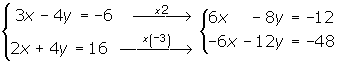
2 Wir addieren die untere Gleichung mit der oberen Gleichung und lösen die Gleichung.
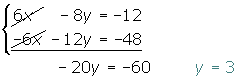
3 Wir setzen den Wert für y in eine der 2 Ausgangsgleichungen ein, in diesem Fall in die zweite.
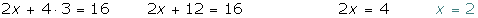
4 Die Lösung ist:
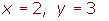
Die Gleichungen direkt addieren (oder subtrahieren)
Da es bei dieser Gleichung möglich ist, 
ohne Multiplikation zu eliminieren, können wir die Gleichungen ohne Vorbereitung addieren.
1 Wir addieren Glied für Glied:
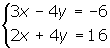
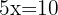
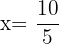
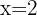
2 Wir setzen den Wert für x in eine der 2 Ausgangsgleichungen ein; in diesem Fall in die erste Gleichung.
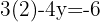
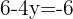
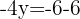
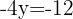
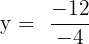
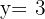
Wir stellen fest, dass die Lösungen in beiden Fällen gleich sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
