Mit dem Satz von Kronecker-Capelli lässt sich die Art der Lösung eines Systems aus 
linearen Gleichungen mit 
Unbekannten bestimmen, ausgehend von der Berechnung des Rangs der durch die Koeffizienten gebildeten Matrix 
und des Rangs der um die konstanten Glieder erweiterten Matrix 
.
Der Satz von Kronecker-Capelli - Grundlagen
Gegeben ist die Koeffizientenmatrix und die erweiterte Matrix des Systems aus linearen Gleichungen mit Unbekannten. Wenn 
und 
jeweils der Rang von und sind, gilt:
Das System ist lösbar, wenn die Ränge übereinstimmen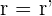 
. Außerdem, wenn 
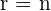, ist das System eindeutig lösbar. Das heißt, es hat eine einzige Lösung.
Wenn das System lösbar ist, 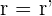, aber 
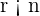, ist das System mehrdeutig lösbar. Das heißt, es hat unendlich viele Lösungen.
Das System ist nicht lösbar, wenn die Ränge unterschiedlich sind, also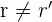 
. Das heißt, das System hat keine Lösung.
Anwendung des Satzes von Kronecker-Capelli
Wir sehen uns folgendes Gleichungssystem an. Löse es, sofern möglich.
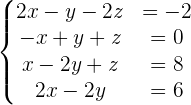
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
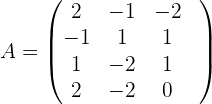
Der Rang ist höher als 1, somit
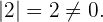
Der Rang ist höher als 2, weil
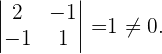
Der Rang ist höher als 3, weil
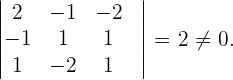
Wenn der Rang höher als 4 ist, können wir keine Berechnung vornehmen, weil die Matrix keine 
Matrix ist. Deshalb gilt 
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
Da
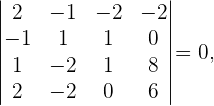
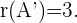
3 Wir wenden den Satz von Kronecker-Capelli an. Das System ist eindeutig lösbar:
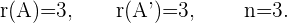
4 Da das System eindeutig lösbar ist, können wir es entweder mit der Cramerschen Regel oder dem Gaußschen Verfahren lösen. Da die vierte Zeile der Matrix eine lineare Kombination aus den anderen drei Zeilen ist, nehmen wir das Untersystem von 
und seine entsprechende Matrix.
In diesem Fall lösen wir das System mit der Cramerschen Regel.
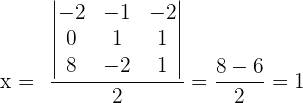
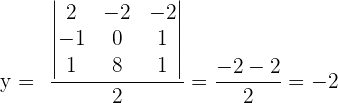
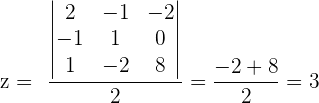
Somit gilt für das ursprüngliche System Folgendes: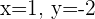 
und 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
